Difference between revisions of "Contact transformation"
| Line 1: | Line 1: | ||
A transformation of curves in the plane under which tangent curves are taken into tangent curves. A contact transformation of surfaces in space is defined similarly. A simple example of a contact transformation is the Legendre transformation (cf. [[Legendre transform|Legendre transform]]). | A transformation of curves in the plane under which tangent curves are taken into tangent curves. A contact transformation of surfaces in space is defined similarly. A simple example of a contact transformation is the Legendre transformation (cf. [[Legendre transform|Legendre transform]]). | ||
| − | More generally, a contact transformation is a diffeomorphism | + | More generally, a contact transformation is a diffeomorphism $f$ of a contact manifold (that is, a manifold $M^{2n+1}$ endowed with a [[contact structure]] with a form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025480/c0254803.png" />), such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025480/c0254804.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025480/c0254805.png" /> is a non-zero function on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025480/c0254806.png" />. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025480/c0254807.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025480/c0254808.png" /> is called a strict contact transformation. A vector field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025480/c0254809.png" /> on a contact manifold is called a contact (or strict contact) infinitesimal transformation if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025480/c02548010.png" /> (or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025480/c02548011.png" />), where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025480/c02548012.png" /> is the [[Lie derivative|Lie derivative]] along <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c025/c025480/c02548013.png" />. Contact transformations are sometimes called tangency transformations. |
====References==== | ====References==== | ||
Revision as of 14:05, 26 April 2023
A transformation of curves in the plane under which tangent curves are taken into tangent curves. A contact transformation of surfaces in space is defined similarly. A simple example of a contact transformation is the Legendre transformation (cf. Legendre transform).
More generally, a contact transformation is a diffeomorphism $f$ of a contact manifold (that is, a manifold $M^{2n+1}$ endowed with a contact structure with a form 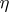 ), such that
), such that  , where
, where 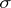 is a non-zero function on
is a non-zero function on  . When
. When 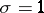 ,
, 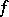 is called a strict contact transformation. A vector field
is called a strict contact transformation. A vector field 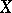 on a contact manifold is called a contact (or strict contact) infinitesimal transformation if
on a contact manifold is called a contact (or strict contact) infinitesimal transformation if 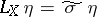 (or
(or 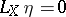 ), where
), where 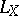 is the Lie derivative along
is the Lie derivative along 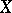 . Contact transformations are sometimes called tangency transformations.
. Contact transformations are sometimes called tangency transformations.
References
| [1] | P.K. Rashevskii, "Geometric theory of partial differential equations" , Moscow-Leningrad (1947) (In Russian) |
| [2] | L.P. Eisenhart, "Riemannian geometry" , Princeton Univ. Press (1949) |
| [3] | S.E. Cohn-Vossen, "Some problems of differential geometry in the large" , Moscow (1959) (In Russian) |
| [4] | C. Godbillon, "Géométrie différentielle et mécanique analytique" , Hermann (1969) |
| [5] | Itogi Nauk. Algebra. Topol. Geom. 1967 (1969) pp. 127–188 |
Comments
Historically the term contact transformation was first used for "transformations" which map a contact element in 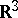 onto another contact element. A contact element at that time was defined as a point in
onto another contact element. A contact element at that time was defined as a point in 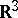 together with a plane passing through that point. The general theory of contact transformations was introduced by S. Lie in his studies of the reduction of Pfaffian forms (cf. Pfaffian equation). In this setting a contact transformation is a mapping
together with a plane passing through that point. The general theory of contact transformations was introduced by S. Lie in his studies of the reduction of Pfaffian forms (cf. Pfaffian equation). In this setting a contact transformation is a mapping
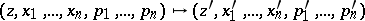 |
such that 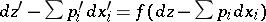 for some nowhere-vanishing function
for some nowhere-vanishing function 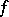 .
.
References
| [a1] | P. Libermann, C.-M. Marle, "Symplectic geometry and analytical mechanics" , Reidel (1987) (Translated from French) |
Contact transformation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contact_transformation&oldid=53868