Condensing operator

An operator 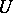, generally non-linear, defined on the set 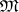of all subsets of a set 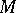in a normed vector space , with values in a normed vector space 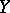, such that 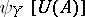— the measure of non-compactness of the set 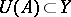— is less than the measure of non-compactness 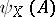for any non-compact set 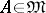. Here, the measures of non-compactness may be the same in both cases or different. For example, as 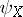and 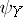one may take the Kuratowski measure of non-compactness: .

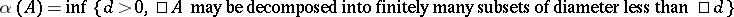For a continuous condensing operator many constructions and facts of the theory of completely-continuous operators can be carried over, for instance, the rotation of contracting vector fields, the fixed-point principle of contraction operators, etc.

References

[1]	B.N. Sadovskii, "Limit-compact and condensing operators" Russian Math. Surveys , 27 (1972) pp. 85–155 Uspekhi Mat. Nauk , 27 : 1 (1972) pp. 81–146
[2]	C. Kuratowski, "Sur les espaces complets" Fund. Math. , 15 (1930) pp. 301–309