Complexification of a Lie algebra
 over
over 
The complex Lie algebra  that is the tensor product of the algebra
that is the tensor product of the algebra  with the complex field
with the complex field  over the field of real numbers
over the field of real numbers  :
:
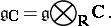 |
Thus, the complexification of the Lie algebra  is obtained from
is obtained from 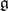 by extending the field of scalars from
by extending the field of scalars from 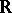 to
to 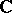 . As elements of the algebra
. As elements of the algebra  one can consider pairs
one can consider pairs 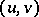 ,
, 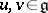 ; the operations in
; the operations in  are then defined by the formulas:
are then defined by the formulas:
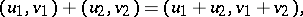 |
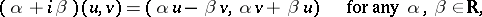 |
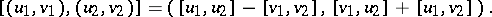 |
The algebra  is also called the complex hull of the Lie algebra
is also called the complex hull of the Lie algebra 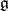 .
.
Certain important properties of an algebra are preserved under complexification: 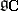 is nilpotent, solvable or semi-simple if and only if
is nilpotent, solvable or semi-simple if and only if  has this property. However, simplicity of
has this property. However, simplicity of  does not, in general, imply that of
does not, in general, imply that of 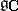 .
.
The notion of the complexification of a Lie algebra is closely related to that of a real form of a complex Lie algebra (cf. Form of an (algebraic) structure). A real Lie subalgebra 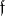 of a complex Lie algebra
of a complex Lie algebra  is called a real form of
is called a real form of 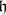 if each element
if each element  is uniquely representable in the form
is uniquely representable in the form 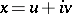 , where
, where  . The complexification of
. The complexification of 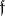 is naturally isomorphic to
is naturally isomorphic to 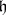 . Not every complex Lie algebra has a real form. On the other hand, a given complex Lie algebra may, in general, have several non-isomorphic real forms. Thus, the Lie algebra of all real matrices of order
. Not every complex Lie algebra has a real form. On the other hand, a given complex Lie algebra may, in general, have several non-isomorphic real forms. Thus, the Lie algebra of all real matrices of order  and the Lie algebra of all anti-Hermitian matrices of order
and the Lie algebra of all anti-Hermitian matrices of order  are non-isomorphic real forms of the Lie algebra of all complex matrices of order
are non-isomorphic real forms of the Lie algebra of all complex matrices of order  (which also has other real forms).
(which also has other real forms).
References
| [1] | M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian) |
| [2] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) |
| [3] | F. Gantmakher, "On the classification of real simple Lie groups" Mat. Sb. , 5 : 2 (1939) pp. 217–250 |
Complexification of a Lie algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complexification_of_a_Lie_algebra&oldid=12632