Completely-continuous operator
completely-continuous mapping
A continuous operator  , acting from a Banach space
, acting from a Banach space  into another space
into another space  , that transforms a weakly-convergent sequence in
, that transforms a weakly-convergent sequence in  to a norm-convergent sequence in
to a norm-convergent sequence in  . It is assumed that the space
. It is assumed that the space  is separable (for
is separable (for  this is not a necessary condition; however, the image of a completely-continuous operator is always separable). In other words, an operator
this is not a necessary condition; however, the image of a completely-continuous operator is always separable). In other words, an operator  is completely-continuous if it maps an arbitrary bounded subset of
is completely-continuous if it maps an arbitrary bounded subset of  into a compact subset of
into a compact subset of 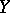 . The class of completely-continuous operators is the most important class of the set of compact operators (cf. Compact operator), which contains, in particular, all compact additive operators.
. The class of completely-continuous operators is the most important class of the set of compact operators (cf. Compact operator), which contains, in particular, all compact additive operators.
(Linear) completely-continuous operators were defined and their simplest properties were established by D. Hilbert [1] in 1904–1906 for the spaces 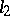 and
and 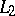 (cf. Hilbert space), by F. Riesz [2] (the definition in terms of compactness), and, for the general case, by S.S. Banach [3] (the definition in terms of sequences). The term "compact operator" has been employed more frequently in recent times, in connection with its appearance in more general topological vector spaces instead of Banach spaces.
(cf. Hilbert space), by F. Riesz [2] (the definition in terms of compactness), and, for the general case, by S.S. Banach [3] (the definition in terms of sequences). The term "compact operator" has been employed more frequently in recent times, in connection with its appearance in more general topological vector spaces instead of Banach spaces.
References
| [1] | D. Hilbert, "Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen" , Chelsea, reprint (1953) |
| [2] | F. Riesz, "Sur les opérations fonctionelles linéaires" C.R. Acad. Sci. Paris Sér. I Math. , 149 (1909) pp. 974–977 |
| [3] | S.S. Banach, "Théorie des opérations linéaires" , Hafner (1932) |
Comments
The term "completely-continuous operator" is in fact not used anymore in Western literature and has been replaced by the term "compact operator" .
References
| [a1] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) |
| [a2] | A.E. Taylor, D.C. Lay, "Introduction to functional analysis" , Wiley (1980) |
Completely-continuous operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Completely-continuous_operator&oldid=16228