Complementary series (of representations)
The family of irreducible continuous unitary representations of a locally compact group 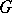 , the non-zero matrix elements of which cannot be approximated by finite linear combinations of matrix elements of the regular representation of
, the non-zero matrix elements of which cannot be approximated by finite linear combinations of matrix elements of the regular representation of 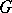 in the topology of uniform convergence on compact sets in
in the topology of uniform convergence on compact sets in 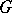 . The complementary series of the group
. The complementary series of the group 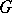 is non-empty if and only if
is non-empty if and only if 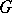 is not amenable, i.e. if the space
is not amenable, i.e. if the space 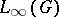 contains no non-trivial left-invariant mean [2]. A connected Lie group
contains no non-trivial left-invariant mean [2]. A connected Lie group 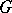 has a non-empty complementary series if and only if the semi-simple quotient group of
has a non-empty complementary series if and only if the semi-simple quotient group of 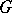 by its maximal connected solvable normal subgroup is non-compact (cf. Levi–Mal'tsev decomposition). A complementary series was first discovered for the complex classical groups [1]. At the time of writing (1987) complementary series have been fully described only for certain locally compact groups. Certain problems in number theory (see, for example, [5]) are equivalent to problems in the theory of representations connected with the complementary series of adèle groups of linear algebraic groups.
by its maximal connected solvable normal subgroup is non-compact (cf. Levi–Mal'tsev decomposition). A complementary series was first discovered for the complex classical groups [1]. At the time of writing (1987) complementary series have been fully described only for certain locally compact groups. Certain problems in number theory (see, for example, [5]) are equivalent to problems in the theory of representations connected with the complementary series of adèle groups of linear algebraic groups.
References
| [1] | I.M. Gel'fand, M.A. Naimark, "Unitäre Darstellungen der klassischen Gruppen" , Akademie Verlag (1957) (Translated from Russian) |
| [2] | F.P. Greenleaf, "Invariant means on topological groups and their applications" , v. Nostrand (1969) |
| [3] | M.A. Naimark, "Linear representations of the Lorentz group" , Macmillan (1964) (Translated from Russian) |
| [4] | B. Kostant, "On the existence and irreducibility of certain series of representations" Bull. Amer. Math. Soc. , 75 (1969) pp. 627–642 |
| [5] | H. Petersson, "Zur analytische Theorie der Grenzkreisgruppen I" Math. Ann. , 115 (1937–1938) pp. 23–67 |
Comments
In the theory of semi-simple Lie groups the notion of a complementary series representation often is introduced in a different fashion, viz. as a generalized principal series representation (cf. Continuous series of representations) that is (infinitesimally) unitary.
References
| [a1] | A.W. Knapp, "Representation theory of semisimple groups" , Princeton Univ. Press (1986) |
Complementary series (of representations). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complementary_series_(of_representations)&oldid=14974