Cohomology of algebras
The groups
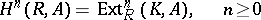 |
(see Functor 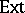 ), where
), where 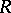 is an associative algebra over a commutative ring
is an associative algebra over a commutative ring 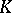 with a fixed
with a fixed  -algebra homomorphism
-algebra homomorphism 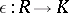 (augmentation) enabling one to regard
(augmentation) enabling one to regard 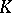 as an
as an 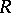 -module, and where
-module, and where 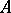 is an
is an 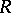 -module. This definition encompasses many cohomology theories of certain types of (universal) algebras.
-module. This definition encompasses many cohomology theories of certain types of (universal) algebras.
Cohomology groups of groups in all dimensions were introduced in the 1940s first by S. Eilenberg and S. MacLane [3] in connection with topological investigations, and by D.K. Faddeev [5] from a purely algebraic point of view — as groups of classes of generalized quotient systems. Cohomology groups in small dimensions were studied earlier in one form or another (see [1], [2], [4]).
Examples of cohomology groups.
1) If 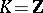 is the ring of integers,
is the ring of integers,  is a group,
is a group, 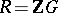 is the group ring of
is the group ring of 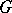 over
over 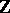 , and
, and
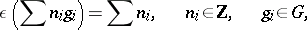 |
then the groups 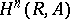 are called the cohomology groups of the group
are called the cohomology groups of the group 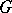 with coefficients (or values) in the
with coefficients (or values) in the 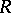 -module
-module 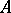 ; they are denoted by
; they are denoted by  . Instead of a group
. Instead of a group 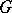 one can consider a monoid
one can consider a monoid 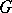 , and obtain the analogous cohomology groups
, and obtain the analogous cohomology groups 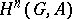 of the monoid
of the monoid 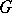 .
.
2) If 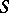 is an associative
is an associative 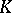 -algebra,
-algebra, 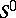 is the opposite
is the opposite  -algebra and
-algebra and
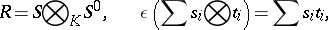 |
then the groups 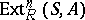 are called the cohomology groups of the associative algebra
are called the cohomology groups of the associative algebra  with coefficients in the
with coefficients in the 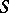 -bimodule
-bimodule 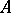 (that is, in the
(that is, in the  -module
-module 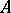 ); they are denoted by
); they are denoted by 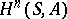 . If
. If 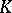 is a field, then the groups
is a field, then the groups 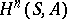 are called the Hochschild cohomology groups of the
are called the Hochschild cohomology groups of the 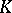 -algebra
-algebra  .
.
3) If 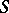 is a Lie algebra over a field
is a Lie algebra over a field 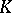 and
and 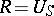 is its universal enveloping algebra with augmentation
is its universal enveloping algebra with augmentation 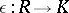 , then the groups
, then the groups 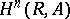 are called the cohomology groups of the Lie algebra
are called the cohomology groups of the Lie algebra 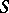 with coefficients in the
with coefficients in the 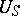 -module
-module 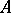 (that is, in the Lie
(that is, in the Lie  -module
-module 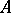 ); they are denoted by
); they are denoted by 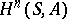 .
.
The cohomology groups for 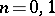 and 2 have, in a number of cases, simple interpretations.
and 2 have, in a number of cases, simple interpretations.
a) If 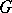 is a group, then
is a group, then 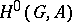 is isomorphic to the group
is isomorphic to the group
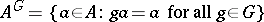 |
of fixed elements; 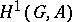 is isomorphic to the quotient group
is isomorphic to the quotient group 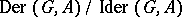 , where
, where
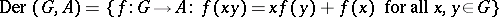 |
is the group of derivations (or crossed homomorphisms),
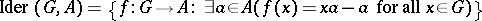 |
is the group of inner derivations (or principal crossed homomorphisms); here, the sequence
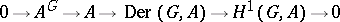 |
is exact; for an Abelian group 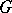 ,
, 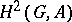 is isomorphic to the group of extensions of
is isomorphic to the group of extensions of  by
by 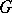 (see Baer multiplication); the third cohomology group of
(see Baer multiplication); the third cohomology group of 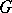 is connected with obstructions to extensions (see [9], Chapt. IV).
is connected with obstructions to extensions (see [9], Chapt. IV).
b) If 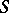 is an associative
is an associative 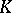 -algebra, then
-algebra, then 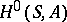 is isomorphic to the group
is isomorphic to the group
 |
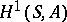 is isomorphic to the quotient group
is isomorphic to the quotient group
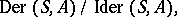 |
where
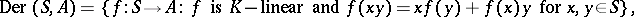 |
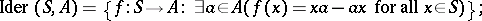 |
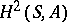 describes the extensions of the
describes the extensions of the 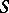 -bimodule
-bimodule 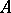 by the ring
by the ring 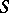 (see [14]).
(see [14]).
c) If 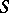 is a Lie algebra, then
is a Lie algebra, then 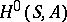 is isomorphic to the
is isomorphic to the 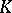 -module
-module 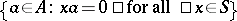 ;
;  is isomorphic to the quotient group
is isomorphic to the quotient group
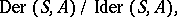 |
where
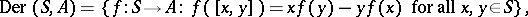 |
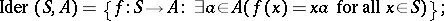 |
the second cohomology group  of a Lie algebra corresponds to the
of a Lie algebra corresponds to the 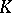 -split extensions of Lie algebras (see [6], Chapt. XIV); in certain cases the elements of
-split extensions of Lie algebras (see [6], Chapt. XIV); in certain cases the elements of 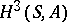 are obstructions in the extension problem.
are obstructions in the extension problem.
Cohomology groups find extensive application in various branches of algebra. E.g. if 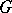 is a group and
is a group and 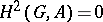 for all
for all 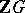 -modules
-modules 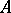 , then
, then 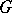 is free (Stalling's theorem, see Homological dimension). If
is free (Stalling's theorem, see Homological dimension). If 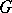 is a finite group and
is a finite group and 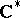 is the multiplicative group of the complex field, then the group
is the multiplicative group of the complex field, then the group  is called the Schur multiplier of
is called the Schur multiplier of 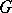 . It plays an important role in the study of central extensions of groups and in the theory of projective representations of finite groups [1]. If
. It plays an important role in the study of central extensions of groups and in the theory of projective representations of finite groups [1]. If 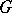 is a group,
is a group, 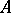 a
a 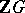 -module and
-module and 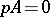 for a prime number
for a prime number 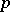 , then
, then
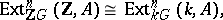 |
where 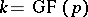 is the field of
is the field of 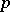 elements. If
elements. If 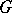 is a finite
is a finite 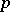 -group, then
-group, then 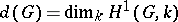 is the minimum number of generators of
is the minimum number of generators of  , and
, and  is the minimum number of defining relations for
is the minimum number of defining relations for  considered as a pro-
considered as a pro-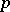 -group;
-group; 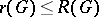 , where
, where 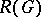 is the minimum number of defining relations of the discrete group
is the minimum number of defining relations of the discrete group  . The fact that
. The fact that  tends to infinity as
tends to infinity as 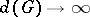 leads to a negative solution of the class field tower problem (cf. Class field theory), the Kurosh problem on nil algebras (cf. Nil algebra) and the unrestricted Burnside problem [10].
leads to a negative solution of the class field tower problem (cf. Class field theory), the Kurosh problem on nil algebras (cf. Nil algebra) and the unrestricted Burnside problem [10].
If 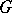 is a profinite group and
is a profinite group and 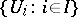 is the family of its open normal subgroups, then the group
is the family of its open normal subgroups, then the group
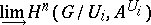 |
is called the  -th cohomology group of the profinite group
-th cohomology group of the profinite group 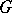 with coefficients in the
with coefficients in the 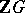 -module
-module 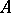 ; it is denoted by
; it is denoted by 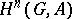 . If
. If 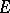 is a Galois extension of a field
is a Galois extension of a field 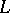 with Galois group
with Galois group 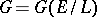 , then
, then 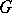 is profinite; in this case the groups
is profinite; in this case the groups 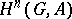 are called Galois cohomology groups. An important role is played by the groups
are called Galois cohomology groups. An important role is played by the groups  where
where  is the multiplicative group of
is the multiplicative group of 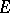 . E.g.
. E.g. 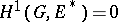 , and a corollary of this fact is Hilbert's theorem 90 (on cyclic extensions). If
, and a corollary of this fact is Hilbert's theorem 90 (on cyclic extensions). If 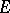 is the separable closure of
is the separable closure of 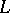 , then
, then 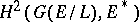 is called the Brauer group of the field
is called the Brauer group of the field 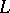 (see Brauer group). At present (1987) a Galois theory of commutative rings is being developed in which an essential part is played by the Galois cohomology of commutative rings and by the Brauer group.
(see Brauer group). At present (1987) a Galois theory of commutative rings is being developed in which an essential part is played by the Galois cohomology of commutative rings and by the Brauer group.
If 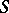 is an associative algebra, then
is an associative algebra, then 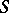 is rigid if
is rigid if  (see Deformation of an algebra).
(see Deformation of an algebra).
In a sense, the cohomology groups 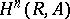 are dual to the homology groups
are dual to the homology groups
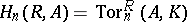 |
of the associative 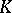 -algebra
-algebra 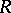 with coefficients in an
with coefficients in an 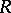 -module
-module 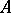 . If
. If 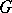 is a group,
is a group, 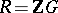 and
and 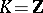 , then the groups
, then the groups 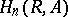 are called the homology groups of the group
are called the homology groups of the group 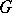 with coefficients in the
with coefficients in the 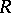 -module
-module 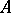 ; they are denoted by
; they are denoted by 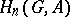 . If
. If 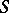 is an associative
is an associative 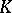 -algebra and
-algebra and 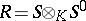 , then the groups
, then the groups 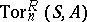 are called the homology groups of the associative algebra
are called the homology groups of the associative algebra 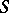 with coefficients in the
with coefficients in the 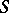 -bimodule
-bimodule 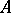 ; they are denoted by
; they are denoted by 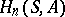 . If
. If 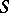 is a Lie algebra and
is a Lie algebra and 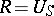 is its universal enveloping algebra, the groups
is its universal enveloping algebra, the groups 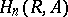 are called the homology groups of the Lie algebra
are called the homology groups of the Lie algebra 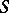 with coefficients in the Lie
with coefficients in the Lie 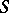 -module
-module 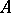 ; they are denoted by
; they are denoted by 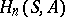 . In a number of cases, the homology groups in small dimensions have a simple interpretation. Thus, if
. In a number of cases, the homology groups in small dimensions have a simple interpretation. Thus, if 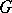 is a group, then
is a group, then 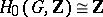 and
and 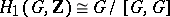 .
.
If in an Abelian category the functor 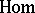 has derived functor
has derived functor 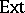 , and the functor
, and the functor  together with its derived functor
together with its derived functor 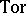 are also defined, then the above scheme defines a cohomology and homology theory in this category. A very general approach to the construction of cohomology theories can be developed using co-triples [11]. The concept of a (co-)triple arose in the analysis of the minimal tools that are necessary for the construction of simplicial resolutions. A triple
are also defined, then the above scheme defines a cohomology and homology theory in this category. A very general approach to the construction of cohomology theories can be developed using co-triples [11]. The concept of a (co-)triple arose in the analysis of the minimal tools that are necessary for the construction of simplicial resolutions. A triple 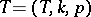 in a category
in a category 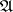 is a functor
is a functor 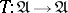 together with two natural transformations of functors
together with two natural transformations of functors 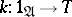 ,
,  , subject to the conditions
, subject to the conditions
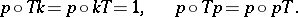 |
The concept of a co-triple is dual to this, that is, it is obtained by reversing arrows. If an object 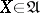 and a morphism
and a morphism 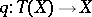 are such that
are such that 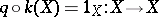 and
and 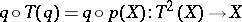 , then the pair
, then the pair 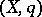 is called a
is called a 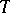 -algebra. Let
-algebra. Let 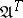 be the category of
be the category of 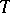 -algebras. If
-algebras. If 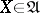 , then
, then 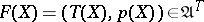 . This defines a functor
. This defines a functor 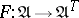 (in a sense,
(in a sense, 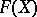 is a free object over
is a free object over 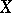 ). Let
). Let  be the functor that forgets the
be the functor that forgets the 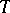 -structure. Then
-structure. Then 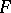 and
and  are adjoint functors (cf. Adjoint functor),
are adjoint functors (cf. Adjoint functor), 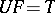 , and
, and 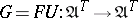 , together with
, together with 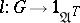 ,
, 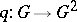 , defines a co-triple
, defines a co-triple 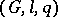 and a complex
and a complex
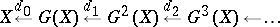 |
with differentiation 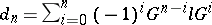 (this complex is an analogue of the canonical free resolution of the object
(this complex is an analogue of the canonical free resolution of the object 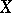 ). If
). If 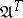 is an Abelian category and the complex so obtained is acyclic, the standard application of the functor
is an Abelian category and the complex so obtained is acyclic, the standard application of the functor 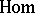 (or
(or 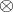 ) gives rise to the construction of the cohomology groups (or homology groups) of the object
) gives rise to the construction of the cohomology groups (or homology groups) of the object 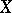 . In general it is necessary to construct a new Abelian category of
. In general it is necessary to construct a new Abelian category of 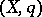 -modules over the
-modules over the 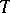 -algebra
-algebra 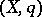 , on which there is a natural co-triple structure enabling one to construct groups, which are then called the cohomology groups of the original category (analogous to the construction of cohomology groups for the categories of groups, associative algebras and Lie algebras). This scheme embraces the cohomology of groups, associative algebras and Lie algebras, as well as a number of other cohomology theories (Harrison cohomology of commutative algebras, André–Quillen cohomology, Amitsur cohomology, etc; see [8]).
, on which there is a natural co-triple structure enabling one to construct groups, which are then called the cohomology groups of the original category (analogous to the construction of cohomology groups for the categories of groups, associative algebras and Lie algebras). This scheme embraces the cohomology of groups, associative algebras and Lie algebras, as well as a number of other cohomology theories (Harrison cohomology of commutative algebras, André–Quillen cohomology, Amitsur cohomology, etc; see [8]).
All the constructions specified here relate to some Abelian category. At the same time, a number of mathematical disciplines (for example, the theory of group extensions) require the construction of cohomology theories with coefficients in a non-Abelian category (for example, in a non-Abelian  -module
-module 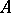 in the case of a group
in the case of a group 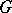 ) (see [8], [11]). The starting-point for the construction of various non-Abelian cohomology theories of algebras is the interpretation of cohomology in dimension 0 and 1, but certain aspects of the classical theory have to be relinquished (group structures on cohomology, etc.). Cohomology of topological algebraic structures has been considered (for example, the cohomology of topological groups [5], Banach algebras, etc.).
) (see [8], [11]). The starting-point for the construction of various non-Abelian cohomology theories of algebras is the interpretation of cohomology in dimension 0 and 1, but certain aspects of the classical theory have to be relinquished (group structures on cohomology, etc.). Cohomology of topological algebraic structures has been considered (for example, the cohomology of topological groups [5], Banach algebras, etc.).
References
| [1] | J. Schur, "Untersuchungen über die Darstellung der endlichen Gruppen durch gebrochene lineare Substitutionen" J. Reine Angew. Math. , 132 (1907) pp. 85–137 |
| [2] | R. Baer, "Erweiterung von Gruppen und ihren Isomorphismen" Math. Z. , 38 (1934) pp. 374–416 |
| [3] | S. Eilenberg, S. MacLane, "Relations between homology and homotopy groups" Proc. Nat. Acad. Sci. USA , 29 (1943) pp. 155–158 |
| [4] | H. Hopf, "Ueber die Bettischen Gruppen, die zu einer beliebigen Gruppe gehören" Comment. Math. Helv. , 17 (1944–1945) pp. 39–79 |
| [5] | D.K. Faddeev, "On quotient systems in Abelian groups with operators" Dokl. Akad. Nauk SSSR , 58 : 3 (1947) pp. 361–364 (In Russian) |
| [6] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) |
| [7] | A. Grothendieck, "Sur quelques points d'algèbre homologique" Tohôku Math. J. , 9 (1957) pp. 119–221 |
| [8] | Itogi Nauk. Algebra 1964 (1966) pp. 203–235 |
| [9] | S. MacLane, "Homology" , Springer (1963) |
| [10] | J.-P. Serre, "Cohomologie Galoisienne" , Springer (1964) |
| [11] | B. Eckmann (ed.) , Seminar on triples and categorical homology theory Zürich, 1966–1967 , Lect. notes in math. , 80 , Springer (1969) |
| [12] | K.W. Gruenberg, "Cohomological topics in group theory" , Springer (1970) |
| [13] | U. Stammbach, "Homology in group theory" , Springer (1973) |
| [14] | R. Fossum, P.A. Griffith, I. Reiten, "Trivial extensions of Abelian categories. Homological algebra of trivial extensions of Abelian categories with applications to ring theory" , Springer (1975) |
Comments
In the definition of Schur multiplier above, the group need not be finite. However, there is no definite agreement on terminology in the case of infinite groups.
In the early 1960s S.U. Chase, D.K. Harrison and A. Rosenberg [a1] developed a Galois theory of commutative rings. In particular, they set up a seven-term exact sequence incorporating Hilbert's theorem 90 and the Brauer group, using Amitsur cohomology as an appropriate generalization of Galois cohomology. In 1982, A.S. Merkurev and A.A. Suslin [a3] showed that for a field 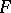 and
and 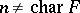 there is an isomorphism between
there is an isomorphism between 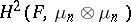 and a group
and a group 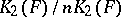 from algebraic
from algebraic 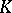 -theory. Here
-theory. Here 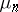 is the group (scheme) of
is the group (scheme) of  -th roots of unity. If
-th roots of unity. If 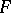 contains a primitive
contains a primitive  -th root of unity this gives an explicit computation of the
-th root of unity this gives an explicit computation of the  -torsion of the Brauer group of
-torsion of the Brauer group of 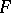 .
.
A comprehensive text on (co)homology of Banach algebras is [a4]. For non-Abelian cohomology cf. [a2].
References
| [a1] | S.U. Chase, D.K. Harrison, A. Rosenberg, "Galois theory and cohomology of commutative rings" , Mem. Amer. Math. Soc. , 52 , Amer. Math. Soc. (1965) |
| [a2] | J. Giraud, "Cohomologie non abélienne" , Springer (1971) |
| [a3] | A.S. Merkurev, A.A. Suslin, "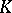 -cohomology of Severi-Brauer varieties and the norm residue homomorphism" Math. USSR-Izv. , 21 (1983) pp. 307–340 Izv. Akad. Nauk SSSR , 46 (1982) pp. 1011–1046 -cohomology of Severi-Brauer varieties and the norm residue homomorphism" Math. USSR-Izv. , 21 (1983) pp. 307–340 Izv. Akad. Nauk SSSR , 46 (1982) pp. 1011–1046 |
| [a4] | A.Ya. [A.Ya. Khelemskii] Helemskii, "Cohomology of Banach and topological spaces" , Reidel (Forthcoming) (Translated from Russian) |
Cohomology of algebras. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cohomology_of_algebras&oldid=15477