Clifford wavelets
A pair of families of Clifford algebra-valued functions satisfying appropriate smoothness, size, cancellation, and orthogonality conditions (cf. also Clifford algebra).
Specifically, denote these two families by  and
and  , where
, where  varies in the set of all dyadic cubes in
varies in the set of all dyadic cubes in  and
and  (the latter indicates that there correspond
(the latter indicates that there correspond  wavelets, left- and right-handed, respectively, to each fixed dyadic cube
wavelets, left- and right-handed, respectively, to each fixed dyadic cube  ; cf. also Wavelet analysis). In the simplest case (that of piecewise-constant, or Haar–Clifford, wavelets) they satisfy the following conditions:
; cf. also Wavelet analysis). In the simplest case (that of piecewise-constant, or Haar–Clifford, wavelets) they satisfy the following conditions:
1)  ,
,  ;
;
2)  ,
,  ;
;
3)  and
and  ;
;
4)  .
.
Here  is a fixed (typically accretive) Clifford-algebra-valued function in
is a fixed (typically accretive) Clifford-algebra-valued function in  and the pairing
and the pairing  is defined as
is defined as
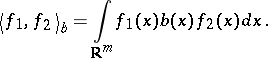 |
Due to the fact that the Clifford algebra-valued measure  in
in 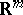 no longer enjoys the usual translation and dilation properties of the Lebesgue measure, one cannot obtain families of functions as such via the familiar translation and dilation operations performed on some initial, fixed, function
no longer enjoys the usual translation and dilation properties of the Lebesgue measure, one cannot obtain families of functions as such via the familiar translation and dilation operations performed on some initial, fixed, function 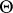 as in the case of ordinary wavelets. However, as the above conditions suggest, everything happens as if one could.
as in the case of ordinary wavelets. However, as the above conditions suggest, everything happens as if one could.
For many applications it is crucial that such families are  -frames, i.e. that
-frames, i.e. that
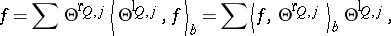 |
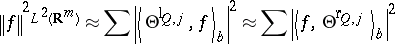 |
for any square-integrable Clifford-algebra-valued function  in
in  .
.
References
| [a1] | P. Auscher, Ph. Tchamitchian, "Bases d'ondelettes sur des courbes corde-arc, noyau de Cauchy et espaces de Hardy associés" Rev. Mat. Iberoamericana , 5 (1989) pp. 139–170 |
| [a2] | M. Mitrea, "Clifford wavelets, singular integrals, and Hardy spaces" , Lecture Notes in Mathematics , 1575 , Springer (1994) |
Clifford wavelets. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Clifford_wavelets&oldid=14068