Choquet boundary
Let 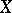 be a compact Hausdorff space (cf. also Compact space), let
be a compact Hausdorff space (cf. also Compact space), let 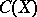 be the Banach algebra of all complex-valued continuous functions on
be the Banach algebra of all complex-valued continuous functions on 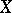 with the supremum norm and let
with the supremum norm and let 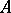 be a linear subspace of
be a linear subspace of 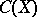 containing the constant functions on
containing the constant functions on 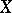 . For
. For 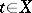 , let
, let 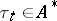 be defined by
be defined by 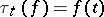 for all
for all 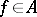 and let
and let 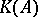 denote the set
denote the set 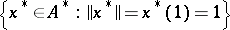 .
.
The Choquet boundary for 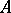 is defined as the set
is defined as the set
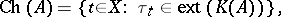 |
where 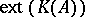 denotes the set of extreme points of
denotes the set of extreme points of 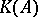 .
.
Other relevant concepts involved in the study of the Choquet boundary are the boundary and the Shilov boundary. A boundary for 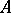 is a subset
is a subset 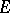 of
of 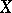 such that for each
such that for each 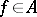 , there exists a
, there exists a 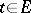 such that
such that 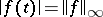 (cf. also Boundary (in the theory of uniform algebras)). If there is a smallest closed boundary for
(cf. also Boundary (in the theory of uniform algebras)). If there is a smallest closed boundary for 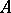 , then it is called the Shilov boundary for
, then it is called the Shilov boundary for  ; it is denoted by
; it is denoted by 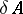 .
.
The motivation for these concepts comes from the classical theory of analytic functions (cf. also Analytic function). If 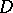 denotes the closed unit disc and
denotes the closed unit disc and 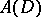 is the linear subspace of
is the linear subspace of 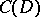 consisting of all complex-valued functions that are continuous on
consisting of all complex-valued functions that are continuous on 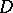 and analytic inside
and analytic inside 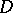 , then, by the maximum-modulus principle, for each
, then, by the maximum-modulus principle, for each 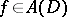 there exists a
there exists a 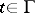 (the unit circle) such that
(the unit circle) such that 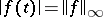 . In fact,
. In fact, 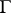 is the smallest closed set having this property. A natural question to ask is: Given an arbitrary linear subspace
is the smallest closed set having this property. A natural question to ask is: Given an arbitrary linear subspace 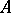 of
of 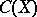 , does there exist a subset of
, does there exist a subset of 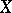 having properties similar to
having properties similar to 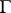 ? Investigations in this direction have led to the introduction of the above concepts.
? Investigations in this direction have led to the introduction of the above concepts.
It is clear from the above discussion that 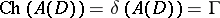 . Also,
. Also, 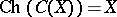 and
and 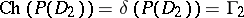 , where
, where 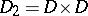 ,
, 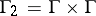 , and
, and 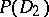 is the uniform closure on
is the uniform closure on 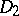 of the algebra of all polynomials in two complex variables (cf. also Uniform space).
of the algebra of all polynomials in two complex variables (cf. also Uniform space).
In general, 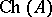 is a boundary of
is a boundary of 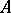 and hence
and hence 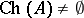 . If, in addition,
. If, in addition, 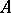 separates the points of
separates the points of 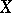 (cf. Uniform algebra), then
(cf. Uniform algebra), then 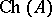 is dense in
is dense in 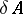 . Also, in this case,
. Also, in this case, 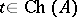 if and only if the
if and only if the 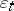 (the unit mass concentrated at
(the unit mass concentrated at 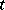 ) is the unique representing measure for
) is the unique representing measure for 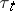 . This equivalent description is used as a definition of Choquet boundary in [a1].
. This equivalent description is used as a definition of Choquet boundary in [a1].
If 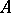 is a subalgebra of
is a subalgebra of 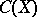 containing the constants and separating the points of
containing the constants and separating the points of 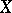 , then the Bishop boundary for
, then the Bishop boundary for 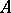 can be defined as the set of all peak points for
can be defined as the set of all peak points for 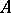 , that is, the set
, that is, the set
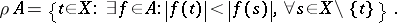 |
For any such algebra 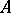 ,
, 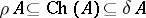 and if, in addition,
and if, in addition, 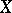 is metrizable (cf. Metrizable space), then
is metrizable (cf. Metrizable space), then 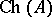 is a
is a 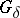 -set. However, if
-set. However, if 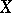 is not metrizable, then the following example [a5] shows that
is not metrizable, then the following example [a5] shows that 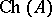 need not even be a Borel set. Let
need not even be a Borel set. Let 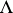 be an uncountable index set and for each
be an uncountable index set and for each 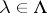 , let
, let 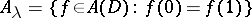 and
and 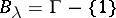 . Then for
. Then for 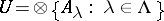 one has
one has 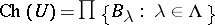 , which is not a Borel set since
, which is not a Borel set since 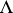 is uncountable.
is uncountable.
If 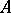 is a uniform algebra (i.e. a closed subalgebra of
is a uniform algebra (i.e. a closed subalgebra of 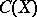 containing the constants and separating the points of
containing the constants and separating the points of 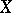 ), then the following are equivalent
), then the following are equivalent
i) 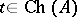 ;
;
ii) for each open neighbourhood 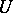 of
of 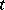 there is an
there is an 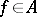 such that
such that 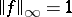 and
and 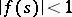 for all
for all 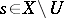 ;
;
iii) there exists a family of peak sets 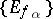 for
for 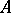 such that
such that
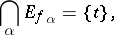 |
where, for 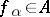 ,
,
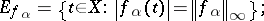 |
iv) given 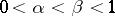 , if
, if 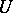 is an open neighbourhood of
is an open neighbourhood of 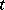 , then there is an
, then there is an 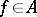 such that
such that 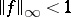 ,
, 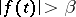 and
and 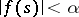 for
for 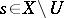 .
.
If 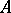 is a uniform algebra and
is a uniform algebra and 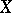 is metrizable, then
is metrizable, then 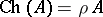 .
.
The concept of Choquet boundary can be extended to any arbitrary commutative Banach algebra via Gel'fand theory. If 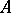 is any commutative Banach algebra (cf. Commutative Banach algebra) with identity, then its maximal ideal space
is any commutative Banach algebra (cf. Commutative Banach algebra) with identity, then its maximal ideal space 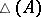 is compact Hausdorff and the Gel'fand representation
is compact Hausdorff and the Gel'fand representation 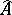 of
of 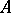 is a subalgebra of
is a subalgebra of 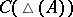 separating the points of
separating the points of 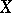 and containing the constants. Hence, one can define the Choquet boundary of
and containing the constants. Hence, one can define the Choquet boundary of 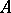 as
as 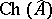 .
.
The concept of Choquet boundary has been extended to real function algebras in [a2].
The notion of Choquet boundary is useful in characterizing onto linear isometries of certain function spaces. In particular, if 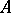 is a subalgebra of
is a subalgebra of 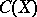 separating points and containing the constants and if
separating points and containing the constants and if  is a linear isometric mapping (linear isometry) of
is a linear isometric mapping (linear isometry) of 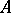 onto
onto 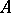 such that
such that 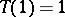 , then one can show that
, then one can show that 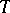 is an algebra isometry of
is an algebra isometry of 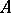 onto
onto 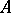 , [a3], p. 243.
, [a3], p. 243.
References
| [a1] | A. Browder, "Introduction to function algebras" , W.A. Benjamin (1969) |
| [a2] | S.H. Kulkarni, B.V. Limaye, "Real function algebras" , M. Dekker (1992) |
| [a3] | R. Larsen, "Banach algebras: an introduction" , M. Dekker (1973) |
| [a4] | R.R. Phelps, "Lectures on Choquet's theorem" , v. Nostrand (1966) |
| [a5] | E.L. Stout, "The theory of uniform algebras" , Bogden and Quigley (1971) |
Choquet boundary. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Choquet_boundary&oldid=42920