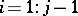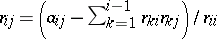Difference between revisions of "Cholesky factorization"
(Importing text file) |
m (fix) |
||
| Line 1: | Line 1: | ||
A symmetric <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201601.png" /> matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201602.png" /> (cf. also [[Symmetric matrix|Symmetric matrix]]) is positive definite if the [[Quadratic form|quadratic form]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201603.png" /> is positive for all non-zero vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201604.png" /> or, equivalently, if all the eigenvalues of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201605.png" /> are positive. Positive-definite matrices have many important properties, not least that they can be expressed in the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201606.png" /> for a non-singular matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201607.png" />. The Cholesky factorization is a particular form of this factorization in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201608.png" /> is upper triangular with positive diagonal elements, and it is usually written as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201609.png" />. In the case of a scalar (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c12016010.png" />), Cholesky factorization corresponds to the fact that a positive number has a positive square root. The factorization is named after A.-L. Cholesky, a French military officer involved in geodesy. It is closely connected with the solution of least-squares problems (cf. also [[Least squares, method of|Least squares, method of]]), since the normal equations that characterize the least-squares solution have a symmetric positive-definite coefficient matrix. | A symmetric <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201601.png" /> matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201602.png" /> (cf. also [[Symmetric matrix|Symmetric matrix]]) is positive definite if the [[Quadratic form|quadratic form]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201603.png" /> is positive for all non-zero vectors <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201604.png" /> or, equivalently, if all the eigenvalues of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201605.png" /> are positive. Positive-definite matrices have many important properties, not least that they can be expressed in the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201606.png" /> for a non-singular matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201607.png" />. The Cholesky factorization is a particular form of this factorization in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201608.png" /> is upper triangular with positive diagonal elements, and it is usually written as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c1201609.png" />. In the case of a scalar (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c12016010.png" />), Cholesky factorization corresponds to the fact that a positive number has a positive square root. The factorization is named after A.-L. Cholesky, a French military officer involved in geodesy. It is closely connected with the solution of least-squares problems (cf. also [[Least squares, method of|Least squares, method of]]), since the normal equations that characterize the least-squares solution have a symmetric positive-definite coefficient matrix. | ||
| − | The Cholesky factorization can be computed by a form of Gaussian elimination that takes advantage of the symmetry and definiteness. Equating <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c12016011.png" /> elements in the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c12016012.png" /> gives | + | The Cholesky factorization can be computed by a form of [[Gaussian elimination]] that takes advantage of the symmetry and definiteness. Equating <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c12016011.png" /> elements in the equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c12016012.png" /> gives |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c12016013.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c12016013.png" /></td> </tr></table> | ||
| Line 7: | Line 7: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c12016014.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c12016014.png" /></td> </tr></table> | ||
| − | These equations can be solved to yield <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c12016015.png" /> a column at a time, according to the following algorithm: | + | These equations can be solved to yield <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c12016015.png" /> a column at a time, according to the following algorithm: |
| + | |||
| + | <table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1">FOR <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c12016016.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">FOR <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c12016017.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c12016018.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">END</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120160/c12016019.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">END</td> </tr> </tbody> </table> | ||
</td></tr> </table> | </td></tr> </table> | ||
Revision as of 18:33, 11 January 2016
A symmetric  matrix
matrix  (cf. also Symmetric matrix) is positive definite if the quadratic form
(cf. also Symmetric matrix) is positive definite if the quadratic form  is positive for all non-zero vectors
is positive for all non-zero vectors  or, equivalently, if all the eigenvalues of
or, equivalently, if all the eigenvalues of  are positive. Positive-definite matrices have many important properties, not least that they can be expressed in the form
are positive. Positive-definite matrices have many important properties, not least that they can be expressed in the form  for a non-singular matrix
for a non-singular matrix  . The Cholesky factorization is a particular form of this factorization in which
. The Cholesky factorization is a particular form of this factorization in which 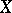 is upper triangular with positive diagonal elements, and it is usually written as
is upper triangular with positive diagonal elements, and it is usually written as  . In the case of a scalar (
. In the case of a scalar (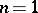 ), Cholesky factorization corresponds to the fact that a positive number has a positive square root. The factorization is named after A.-L. Cholesky, a French military officer involved in geodesy. It is closely connected with the solution of least-squares problems (cf. also Least squares, method of), since the normal equations that characterize the least-squares solution have a symmetric positive-definite coefficient matrix.
), Cholesky factorization corresponds to the fact that a positive number has a positive square root. The factorization is named after A.-L. Cholesky, a French military officer involved in geodesy. It is closely connected with the solution of least-squares problems (cf. also Least squares, method of), since the normal equations that characterize the least-squares solution have a symmetric positive-definite coefficient matrix.
The Cholesky factorization can be computed by a form of Gaussian elimination that takes advantage of the symmetry and definiteness. Equating 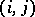 elements in the equation
elements in the equation  gives
gives
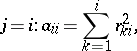 |
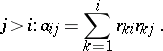 |
These equations can be solved to yield 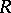 a column at a time, according to the following algorithm:
a column at a time, according to the following algorithm:
<tbody> </tbody>
|
It is the positive definiteness of 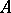 that guarantees that the argument of the square root in this algorithm is always positive.
that guarantees that the argument of the square root in this algorithm is always positive.
It can be shown [a1] that in floating-point arithmetic the computed solution 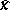 satisfies
satisfies  , where
, where 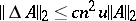 , with
, with  a constant of order
a constant of order 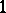 and
and  the unit round-off (or machine precision). Here,
the unit round-off (or machine precision). Here, 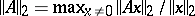 and
and 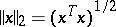 . This excellent numerical stability is essentially due to the equality
. This excellent numerical stability is essentially due to the equality  , which guarantees that
, which guarantees that 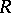 is of bounded norm relative to
is of bounded norm relative to 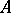 .
.
A variant of Cholesky factorization is the factorization 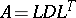 where
where 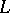 is unit lower triangular and
is unit lower triangular and  is diagonal. This factorization exists for definite matrices and some (but not all) indefinite ones. When
is diagonal. This factorization exists for definite matrices and some (but not all) indefinite ones. When  is positive definite, the Cholesky factor is given by
is positive definite, the Cholesky factor is given by  .
.
A symmetric matrix 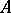 is positive semi-definite if the quadratic form
is positive semi-definite if the quadratic form 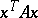 is non-negative for all
is non-negative for all  ; thus,
; thus,  may be singular (cf. also Matrix). For such matrices a Cholesky factorization exists, but
may be singular (cf. also Matrix). For such matrices a Cholesky factorization exists, but 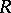 may not display the rank of
may not display the rank of 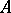 . However, by introducing row and column permutations it is always possible to obtain a factorization
. However, by introducing row and column permutations it is always possible to obtain a factorization
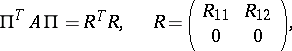 |
where 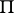 is a permutation matrix,
is a permutation matrix, 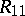 is
is 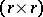 upper triangular with positive diagonal elements, and
upper triangular with positive diagonal elements, and  .
.
Cf. Matrix factorization for more details and references.
References
| [a1] | N.J. Higham, "Accuracy and stability of numerical algorithms" , SIAM (Soc. Industrial Applied Math.) (1996) |
Cholesky factorization. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cholesky_factorization&oldid=37467