Chetaev equations
General canonical equations of the mechanics of a holonomic system, presented in terms of a certain Lie algebra of infinitesimal transformations, and equivalent to the Poincaré equations.
If instead of independent variables  defining real displacements one introduces the quantities
defining real displacements one introduces the quantities
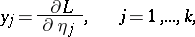 |
where  is the Lagrangian, then the Poincaré equations take the simpler form of the Chetaev equations
is the Lagrangian, then the Poincaré equations take the simpler form of the Chetaev equations
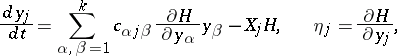 | (1) |
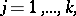 |
where
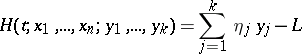 |
is the Hamiltonian. The second group of equations (1) may be replaced by the equations
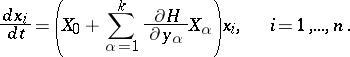 | (2) |
(Cf. Poincaré equations for the operators  .)
.)
Introducing the action function by the formula
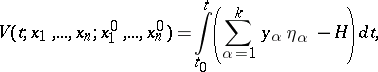 |
where the integration takes place over the real trajectories of the system, one obtains the relations
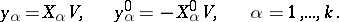 | (3) |
Here the 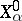 denote the operators
denote the operators  applied to the initial momentum at time
applied to the initial momentum at time  and the initial position of the system
and the initial position of the system  ; and
; and  are the initial values of
are the initial values of 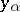 . If the action function is known, then the equations (3) solve the mechanical problem in which the second group of equations (3) defines, in an implicit way, the law of motion of the system.
. If the action function is known, then the equations (3) solve the mechanical problem in which the second group of equations (3) defines, in an implicit way, the law of motion of the system.
The action function satisfies the first-order partial differential equation
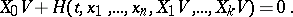 | (4) |
If a complete integral 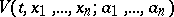 of (4) is known, then the solutions to the Chetaev equations are determined by the relations
of (4) is known, then the solutions to the Chetaev equations are determined by the relations
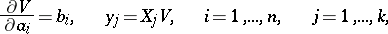 |
where  and
and 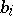 are arbitrary constants, restricted by the
are arbitrary constants, restricted by the 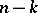 integrability equations of the constraint.
integrability equations of the constraint.
Instead of the variables 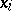 one can consider new variables
one can consider new variables 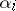 defining the position of the system. Suppose that
defining the position of the system. Suppose that  ,
,  ,
, 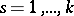 , represent the Lie algebra of a
, represent the Lie algebra of a  -parameter Lie group of continuous transformations in the variables
-parameter Lie group of continuous transformations in the variables 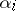 with structure constants
with structure constants  , where
, where 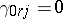 ; and suppose that
; and suppose that 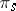 and
and  are variables defining possible and actual displacements, so that for some function
are variables defining possible and actual displacements, so that for some function
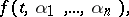 |
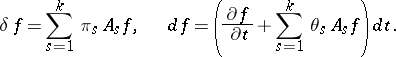 |
The transformation of variables is determined by the characteristic function
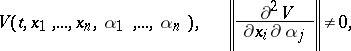 |
and the formulas
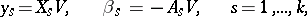 |
together with the integrability equations of the constraints. Such transformations are called canonical transformations, they preserve the canonical form of the equations of motion, in which the Hamilton function in the new variables takes the form
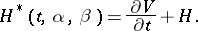 |
(Cf. also Hamiltonian system.) If the characteristic function of the transformation is a complete integral of equation (4) (for  ), then
), then 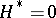 and the Chetaev equations (1) and (2) in the new variables take the form
and the Chetaev equations (1) and (2) in the new variables take the form
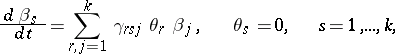 |
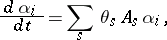 |
that is 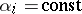 ,
, 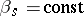 ,
, 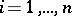 ,
, 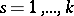 .
.
The linear form  defines the fundamental relative integral invariant of dynamics.
defines the fundamental relative integral invariant of dynamics.
The condition for  to be constant is that the first integral of Chetaev's equations has the form
to be constant is that the first integral of Chetaev's equations has the form
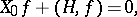 |
where
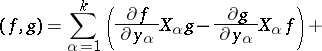 |
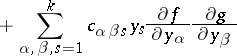 |
defines the Poisson bracket.
If 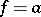 and
and  are first integrals, then
are first integrals, then 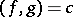 is also an integral (a generalization of the Poisson theorem).
is also an integral (a generalization of the Poisson theorem).
The Chetaev equations were introduced by N.G. Chetaev [1]–[3], who also developed their theory.
References
| [1] | N.G. Chetaev, "Sur les équations de Poincaré" C.R. Acad. Sci. Paris , 185 (1927) pp. 1577–1578 |
| [2] | N.G. Chetaev, "Sur les équations de Poincaré" Dokl. Akad. Nauk SSSR Ser A. : 7 (1928) pp. 103–104 |
| [3] | N.G. Chetaev, "On the equations of Poincaré" Prikl. Mat. i Mekh. , 5 : 2 (1941) pp. 253–262 (In Russian) |
Chetaev equations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chetaev_equations&oldid=14743