Chebyshev theorem
If a function 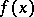 is continuous on
is continuous on 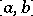 and if
and if
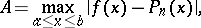 |
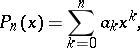 |
then 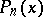 is the polynomial of best uniform approximation for
is the polynomial of best uniform approximation for 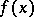 , i.e.
, i.e.
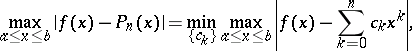 |
if and only if there exist 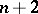 points
points 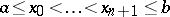 in Chebyshev alternation, which means that the condition
in Chebyshev alternation, which means that the condition
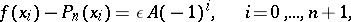 |
is satisfied, where 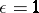 or
or 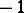 . This theorem was proved by P.L. Chebyshev in 1854 (cf. [1]) in a more general form, namely for the best uniform approximation of functions by rational functions with fixed degrees of the numerator and denominator. Chebyshev's theorem remains valid if instead of algebraic polynomials one considers polynomials
. This theorem was proved by P.L. Chebyshev in 1854 (cf. [1]) in a more general form, namely for the best uniform approximation of functions by rational functions with fixed degrees of the numerator and denominator. Chebyshev's theorem remains valid if instead of algebraic polynomials one considers polynomials
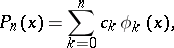 |
where 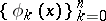 is a Chebyshev system. The criterion formulated in Chebyshev's theorem leads to methods for the approximate construction of polynomials of best uniform (Chebyshev) approximation. In a somewhat different formulation Chebyshev's theorem can be extended to functions of a complex variable (cf. [2]) and to abstract functions (cf. [3]).
is a Chebyshev system. The criterion formulated in Chebyshev's theorem leads to methods for the approximate construction of polynomials of best uniform (Chebyshev) approximation. In a somewhat different formulation Chebyshev's theorem can be extended to functions of a complex variable (cf. [2]) and to abstract functions (cf. [3]).
References
| [1] | P.L. Chebyshev, "Questions on smallest quantities connected with the approximate representation of functions (1859)" , Collected works , 2 , Moscow-Leningrad (1947) pp. 151–238 (In Russian) |
| [2] | A.N. Kolmogorov, "A remark on the polynomials of Chebyshev deviating the least from a given function" Uspekhi Mat. Nauk , 3 : 1 (1948) pp. 216–221 (In Russian) |
| [3] | S.I. Zukhovitskii, S.B. Stechkin, "On the approximation of abstract functions with values in a Banach space" Dokl. Akad. Nauk SSSR , 106 : 5 (1956) pp. 773–776 (In Russian) |
| [4] | V.K. Dzyadyk, "Introduction to the theory of uniform approximation of functions by polynomials" , Moscow (1977) (In Russian) |
Comments
References
| [a1] | G.G. Lorentz, "Approximation of functions" , Holt, Rinehart & Winston (1966) pp. Chapt. 2 |
Chebyshev theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebyshev_theorem&oldid=15464