Difference between revisions of "Chebyshev inequality in probability theory"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
(refs format) |
||
| Line 33: | Line 33: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021890/c02189017.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021890/c02189017.png" /></td> </tr></table> | ||
| − | It has become traditional to consider all these inequalities to be of Chebyshev type, and even to call them Chebyshev inequalities. There is a general principle for obtaining Chebyshev inequalities by imposing conditions on the moments, based on the use of the system of Chebyshev polynomials (cf. | + | It has become traditional to consider all these inequalities to be of Chebyshev type, and even to call them Chebyshev inequalities. There is a general principle for obtaining Chebyshev inequalities by imposing conditions on the moments, based on the use of the system of Chebyshev polynomials (cf. {{Cite|KS}}). For arbitrary random variables the Chebyshev inequalities give precise and best possible bounds, but in certain concrete situations these bounds can be improved. For example, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021890/c02189018.png" /> has a unimodal distribution with mode <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021890/c02189019.png" /> coinciding with the mathematical expectation, then Gauss' inequality holds: |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021890/c02189020.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021890/c02189020.png" /></td> </tr></table> | ||
| Line 59: | Line 59: | ||
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021890/c02189027.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021890/c02189028.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021890/c02189029.png" /> (cf. [[Bernstein inequality|Bernstein inequality]]). Such improvements of Chebyshev inequalities are obtained under additional restrictions on the summands <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021890/c02189030.png" />. | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021890/c02189027.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021890/c02189028.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021890/c02189029.png" /> (cf. [[Bernstein inequality|Bernstein inequality]]). Such improvements of Chebyshev inequalities are obtained under additional restrictions on the summands <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021890/c02189030.png" />. | ||
| − | Multi-dimensional analogues have been obtained of some of the inequalities stated here (cf. | + | Multi-dimensional analogues have been obtained of some of the inequalities stated here (cf. {{Cite|P}}). |
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|C}}|| P.L. Chebyshev, "?", ''Mat. Sb.'' , '''2''' (1867) pp. 1–9 | ||
| + | |- | ||
| + | |valign="top"|{{Ref|M}}|| A.A. Markov, "Wahrscheinlichkeitsrechung" , Teubner (1912) (Translated from Russian) {{MR|}} {{ZBL|39.0292.02}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|K}}|| A.N. Kolmogorov, "Foundations of the theory of probability" , Chelsea, reprint (1950) (Translated from German) {{MR|0032961}} {{ZBL|}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|KS}}|| S. Karlin, V. Studden, "Tchebycheff systems: with applications in analysis and statistics" , Interscience (1966) {{MR|0204922}} {{ZBL|0153.38902}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|P}}|| Yu.V. Prokhorov, "Multivariate distributions: inequalities and limit theorems" ''J. Soviet Math.'' , '''2''' (1974) pp. 475–488 ''Itogi Nauk. i Tekhn. Teor. Veroyatnost. Mat. Stat. Teoret. Kibernet.'' , '''10''' (1972) pp. 5–24 {{MR|}} {{ZBL|0295.60013}} | ||
| + | |} | ||
Revision as of 14:40, 11 May 2012
Bienaymé–Chebyshev inequality
2020 Mathematics Subject Classification: Primary: 60E15 [MSN][ZBL]
An inequality in probability theory that gives a bound on the probability of deviation of a given random variable from its mathematical expectation in terms of its variance. Let  be a random variable with finite mathematical expectation
be a random variable with finite mathematical expectation  and variance
and variance  . Chebyshev's inequality states that for any
. Chebyshev's inequality states that for any  the probability of the event
the probability of the event
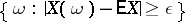 |
does not exceed  , or
, or
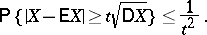 | (1) |
This inequality was discovered independently by I. Bienaymé (1853) and P.L. Chebyshev (1866). In modern literature this inequality is usually referred to as Chebyshev's inequality, possibly because the name of Chebyshev is associated with an application of it in the proof of the law of large numbers (a theorem of Chebyshev).
Chebyshev's inequality is a representative of a whole class of inequalities of this type, the simplest of which asserts that for a non-negative random variable  with finite mathematical expectation
with finite mathematical expectation  ,
,
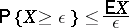 | (2) |
(this is sometimes called Markov's inequality). This implies an inequality for arbitrary random variables, which depends on the moments:
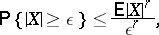 |
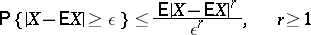 |
(for 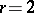 this is just the Chebyshev inequality), and also the more general inequality
this is just the Chebyshev inequality), and also the more general inequality
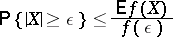 | (3) |
for a non-negative even function 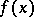 that is non-decreasing for positive
that is non-decreasing for positive  . Inequality (3) indicates a way to obtain new inequalities of the same type, for example the exponential inequality
. Inequality (3) indicates a way to obtain new inequalities of the same type, for example the exponential inequality
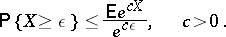 |
It has become traditional to consider all these inequalities to be of Chebyshev type, and even to call them Chebyshev inequalities. There is a general principle for obtaining Chebyshev inequalities by imposing conditions on the moments, based on the use of the system of Chebyshev polynomials (cf. [KS]). For arbitrary random variables the Chebyshev inequalities give precise and best possible bounds, but in certain concrete situations these bounds can be improved. For example, if  has a unimodal distribution with mode
has a unimodal distribution with mode 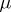 coinciding with the mathematical expectation, then Gauss' inequality holds:
coinciding with the mathematical expectation, then Gauss' inequality holds:
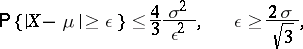 |
where  .
.
The importance of Chebyshev's inequality in probability theory lies not so much in its exactness, but in its simplicity and universality. Chebyshev's inequality and its modifications, applied to sums of random variables, played a large part in the proofs of various forms of the law of large numbers and the law of the iterated logarithm. Chebyshev's inequality for sums of independent random variables has been subject to generalization and improvement in two different directions. The first of these is connected with the transition from the Chebyshev inequality
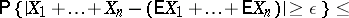 |
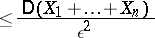 |
to the significantly stronger inequality
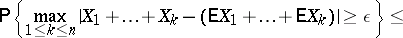 |
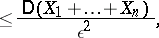 |
which was proved by A.N. Kolmogorov and applied by him to prove the strong law of large numbers (cf. Kolmogorov inequality).
The second direction is concerned with replacing the power in Chebyshev's inequality by something with exponential decay, and leads to the Bernshtein–Kolmogorov inequality:
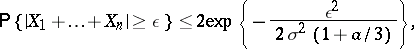 |
where  ,
,  ,
,  (cf. Bernstein inequality). Such improvements of Chebyshev inequalities are obtained under additional restrictions on the summands
(cf. Bernstein inequality). Such improvements of Chebyshev inequalities are obtained under additional restrictions on the summands 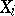 .
.
Multi-dimensional analogues have been obtained of some of the inequalities stated here (cf. [P]).
References
| [C] | P.L. Chebyshev, "?", Mat. Sb. , 2 (1867) pp. 1–9 |
| [M] | A.A. Markov, "Wahrscheinlichkeitsrechung" , Teubner (1912) (Translated from Russian) Zbl 39.0292.02 |
| [K] | A.N. Kolmogorov, "Foundations of the theory of probability" , Chelsea, reprint (1950) (Translated from German) MR0032961 |
| [KS] | S. Karlin, V. Studden, "Tchebycheff systems: with applications in analysis and statistics" , Interscience (1966) MR0204922 Zbl 0153.38902 |
| [P] | Yu.V. Prokhorov, "Multivariate distributions: inequalities and limit theorems" J. Soviet Math. , 2 (1974) pp. 475–488 Itogi Nauk. i Tekhn. Teor. Veroyatnost. Mat. Stat. Teoret. Kibernet. , 10 (1972) pp. 5–24 Zbl 0295.60013 |
Chebyshev inequality in probability theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebyshev_inequality_in_probability_theory&oldid=23594