Difference between revisions of "Character of a semi-group"
(Importing text file) |
m (link) |
||
| Line 1: | Line 1: | ||
''semi-group character'' | ''semi-group character'' | ||
| − | A non-zero homomorphism of a commutative semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021590/c0215901.png" /> with identity into the multiplicative semi-group consisting of all complex numbers of modulus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021590/c0215902.png" />, together with 0. Sometimes a character of a semi-group is understood as a non-zero homomorphism into the multiplicative semi-group of complex numbers of modulus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021590/c0215903.png" />. Both concepts of a character of a semi-group are equivalent if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021590/c0215904.png" /> is a [[Clifford semi-group|Clifford semi-group]]. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021590/c0215905.png" /> of all characters of a semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021590/c0215906.png" /> forms a commutative semi-group with identity (the character semi-group) under pointwise multiplication <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021590/c0215907.png" />, | + | A non-zero homomorphism of a commutative semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021590/c0215901.png" /> with identity into the multiplicative semi-group consisting of all complex numbers of modulus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021590/c0215902.png" />, together with 0. Sometimes a character of a semi-group is understood as a non-zero homomorphism into the multiplicative semi-group of complex numbers of modulus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021590/c0215903.png" />. Both concepts of a character of a semi-group are equivalent if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021590/c0215904.png" /> is a [[Clifford semi-group|Clifford semi-group]]. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021590/c0215905.png" /> of all characters of a semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021590/c0215906.png" /> forms a commutative semi-group with identity (the character semi-group) under [[pointwise multiplication]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021590/c0215907.png" />, |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021590/c0215908.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021590/c0215908.png" /></td> </tr></table> | ||
Revision as of 18:24, 1 December 2014
semi-group character
A non-zero homomorphism of a commutative semi-group 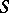 with identity into the multiplicative semi-group consisting of all complex numbers of modulus
with identity into the multiplicative semi-group consisting of all complex numbers of modulus 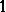 , together with 0. Sometimes a character of a semi-group is understood as a non-zero homomorphism into the multiplicative semi-group of complex numbers of modulus
, together with 0. Sometimes a character of a semi-group is understood as a non-zero homomorphism into the multiplicative semi-group of complex numbers of modulus 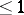 . Both concepts of a character of a semi-group are equivalent if
. Both concepts of a character of a semi-group are equivalent if 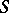 is a Clifford semi-group. The set
is a Clifford semi-group. The set  of all characters of a semi-group
of all characters of a semi-group 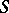 forms a commutative semi-group with identity (the character semi-group) under pointwise multiplication
forms a commutative semi-group with identity (the character semi-group) under pointwise multiplication  ,
,
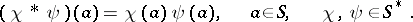 |
An ideal 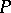 of a semi-group
of a semi-group 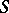 is called totally isolated (prime) if
is called totally isolated (prime) if  is a sub-semi-group. The set of all totally-isolated ideals of a commutative semi-group with identity forms a semi-lattice under the operation of union. This semi-lattice is isomorphic to the semi-lattice of idempotents (see Idempotents, semi-group of) of
is a sub-semi-group. The set of all totally-isolated ideals of a commutative semi-group with identity forms a semi-lattice under the operation of union. This semi-lattice is isomorphic to the semi-lattice of idempotents (see Idempotents, semi-group of) of 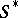 . The characters of a commutative semi-group
. The characters of a commutative semi-group 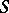 separate the elements of
separate the elements of 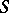 if for any
if for any 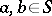 ,
,  , there is a
, there is a 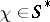 such that
such that 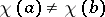 . If
. If  has an identity, then the characters of the semi-group
has an identity, then the characters of the semi-group 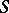 separate the elements of
separate the elements of 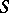 if and only if
if and only if 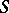 is a separable semi-group. The problem of describing the character semi-group of an arbitrary commutative semi-group with identity reduces to a description of the characters of a semi-group that is a semi-lattice of groups; for a corresponding description when this semi-lattice satisfies a minimum condition see, for example, [1]. An abstract characterization of character semi-groups is in [2].
is a separable semi-group. The problem of describing the character semi-group of an arbitrary commutative semi-group with identity reduces to a description of the characters of a semi-group that is a semi-lattice of groups; for a corresponding description when this semi-lattice satisfies a minimum condition see, for example, [1]. An abstract characterization of character semi-groups is in [2].
For every 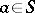 ,
, 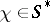 , the mapping
, the mapping 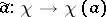 ,
, 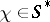 , is a character of the semi-group
, is a character of the semi-group 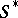 , that is,
, that is, 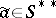 . The mapping
. The mapping 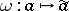 is a homomorphism of
is a homomorphism of 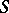 into
into 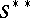 (the so-called canonical homomorphism). If
(the so-called canonical homomorphism). If 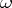 is an isomorphism of
is an isomorphism of 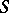 onto
onto 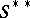 , then one says that the duality theorem holds for
, then one says that the duality theorem holds for  . The duality theorem is true for a commutative semi-group
. The duality theorem is true for a commutative semi-group 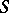 with identity if and only if
with identity if and only if 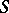 is an inverse semi-group [3]. About duality problems for character semi-groups in the topological case see Topological semi-group.
is an inverse semi-group [3]. About duality problems for character semi-groups in the topological case see Topological semi-group.
References
| [1] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1 , Amer. Math. Soc. (1961) |
| [2] | M.M. Lesokhin, "Characters of commutative semigroups I" Izv. Vuz. Mat. , 8 (1970) pp. 67–74 (In Russian) |
| [3] | C. Austin, "Duality theorems for some commutative semigroups" Trans. Amer. Math. Soc. , 109 : 2 (1963) pp. 245–256 |
Character of a semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Character_of_a_semi-group&oldid=18046