Cauchy problem
One of the fundamental problems in the theory of (ordinary and partial) differential equations: To find a solution (an integral) of a differential equation satisfying what are known as initial conditions (initial data). The Cauchy problem usually appears in the analysis of processes defined by a differential law and an initial state, formulated mathematically in terms of a differential equation and an initial condition (hence the terminology and the choice of notation: The initial data are specified for 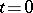 and the solution is required for
and the solution is required for 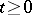 ). Cauchy problems differ from boundary value problems in that the domain in which the desired solution must be defined is not specified in advance. Nevertheless, Cauchy problems, like boundary value problems, are defined by the imposition of limiting conditions for the solution on (part of) the boundary of the domain of definition.
). Cauchy problems differ from boundary value problems in that the domain in which the desired solution must be defined is not specified in advance. Nevertheless, Cauchy problems, like boundary value problems, are defined by the imposition of limiting conditions for the solution on (part of) the boundary of the domain of definition.
The main questions connected with Cauchy problems are as follows:
1) Does there exist (albeit only locally) a solution?
2) If the solution exists, to what space does it belong? In particular, what is its domain of existence?
3) Is the solution unique?
4) If the solution is unique, is the problem well-posed, i.e. is the solution in some sense a continuous function of the initial data?
The simplest Cauchy problem is to find a function 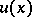 defined on the half-line
defined on the half-line 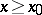 , satisfying a first-order ordinary differential equation
, satisfying a first-order ordinary differential equation
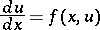 | (1) |
( is a given function) and taking a specified value
is a given function) and taking a specified value 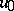 at
at 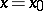 :
:
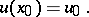 | (2) |
In geometrical terms this means that, considering the family of integral curves of equation (1) in the  -plane, one wishes to find the curve passing through the point
-plane, one wishes to find the curve passing through the point  .
.
The first proposition concerning the existence of such a function (on the assumption that 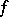 is continuous for all
is continuous for all  and continuously differentiable with respect to
and continuously differentiable with respect to  ) was proved by A.L. Cauchy (1820–1830) and generalized by E. Picard (1891–1896) (who replaced differentiability by a Lipschitz condition with respect to
) was proved by A.L. Cauchy (1820–1830) and generalized by E. Picard (1891–1896) (who replaced differentiability by a Lipschitz condition with respect to  ). It turns out that under those conditions the Cauchy problem has a unique solution which, moreover, depends continuously on the initial data. Modern concepts of the Cauchy problem are essentially a far-reaching generalization of this problem.
). It turns out that under those conditions the Cauchy problem has a unique solution which, moreover, depends continuously on the initial data. Modern concepts of the Cauchy problem are essentially a far-reaching generalization of this problem.
The fact that questions 1) to 4) touch profoundly on the very heart of the matter — i.e. to answer them satisfactorily requires the imposition of certain conditions — is already illustrated in the theory of ordinary differential equations. Thus, a solution of the Cauchy problem for equation (1) with the condition (2), where 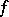 is given on an open set
is given on an open set 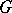 and is only continuous, exists on some interval depending on
and is only continuous, exists on some interval depending on 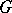 and
and 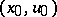 (see Peano theorem), but it need not be unique. The solution need not exist at all points in the domain of definition of
(see Peano theorem), but it need not be unique. The solution need not exist at all points in the domain of definition of  .
.
Repeating the above account almost word for word, one formulates the Cauchy problem for systems of ordinary differential equations, i.e. for an ordinary differential equation of type (1) with initial condition (2), where 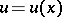 is a function with values in a finite-dimensional vector space
is a function with values in a finite-dimensional vector space 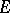 ,
, 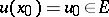 , and
, and  is a function defined in
is a function defined in 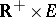 . Here, again, the Picard conditions are sufficient for the existence and uniqueness of the solution and for the problem to be well-posed.
. Here, again, the Picard conditions are sufficient for the existence and uniqueness of the solution and for the problem to be well-posed.
For ordinary differential equations of a higher order,
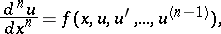 |
the Cauchy problem the initial data of which involve, besides the function itself, the derivatives
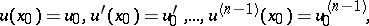 |
can be reduced by the standard device to a corresponding problem of type (1), (2).
In the case of first-order ordinary differential equations which cannot be expressed directly in terms of the derivative of the unknown function (as in equation (1)), the formulation of the Cauchy problem is similar, except that it relies to a high degree on the geometrical interpretation; however, the actual investigation of the equation may be complicated by the impossibility of (even locally) reducing the equation to the normal form (1).
While neither the formulation nor the investigation of the Cauchy problem for an ordinary differential equation involve essential difficulties, the situation is considerably more complicated in the case of partial differential equations (this applies, in particular, to answering questions 1) to 4)). This is true even if the functions involved are sufficiently regular (smooth). A major source of the difficulty is the fact that the space of independent variables is higher-dimensional, resulting in problems of (algebraic) solvability. E.g., consider the Cauchy problem for a system of equations in total differentials,
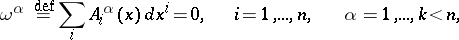 |
such equations being in a sense intermediate between "ordinary" and "partial" differential equations. The problem here is to determine an 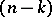 -dimensional integral surface passing through a given point. Then the solvability condition is
-dimensional integral surface passing through a given point. Then the solvability condition is
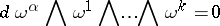 |
(in a neighbourhood of the given point; here 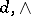 are the symbols for the exterior differential and the exterior product, respectively) (see Frobenius theorem).
are the symbols for the exterior differential and the exterior product, respectively) (see Frobenius theorem).
For linear partial differential equations
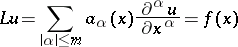 | (3) |
the Cauchy problem may be formulated as follows. In a certain region 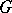 of the variables
of the variables 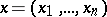 it is required to find a solution satisfying initial conditions, i.e. taking specified values, together with its derivatives of order up to and including
it is required to find a solution satisfying initial conditions, i.e. taking specified values, together with its derivatives of order up to and including  , on some
, on some 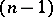 -dimensional hypersurface
-dimensional hypersurface 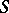 in
in  . This hypersurface is known as the carrier of the initial conditions (or the initial surface). The initial conditions may be given in the form of derivatives of
. This hypersurface is known as the carrier of the initial conditions (or the initial surface). The initial conditions may be given in the form of derivatives of  with respect to the direction of the unit normal
with respect to the direction of the unit normal  to
to 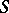 :
:
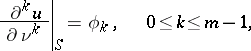 | (4) |
where the 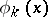 ,
,  , are known functions (Cauchy data).
, are known functions (Cauchy data).
The formulation of the Cauchy problem for non-linear differential equations is similar.
A concept related to the Cauchy problem is that of a non-characteristic surface. If a non-singular coordinate transformation 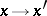 "straightens out" the surface
"straightens out" the surface 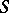 in a neighbourhood of
in a neighbourhood of 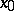 , i.e. it transforms it into a part of the hyperplane
, i.e. it transforms it into a part of the hyperplane 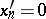 , then the coefficient of
, then the coefficient of  in the transformed equation (3) is proportional to
in the transformed equation (3) is proportional to
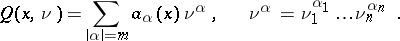 |
The surface 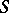 is said to be non-characteristic at the point
is said to be non-characteristic at the point 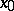 if
if
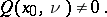 | (5) |
In that case equation (3) may be written in a neighbourhood of 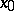 in the so-called normal form:
in the so-called normal form:
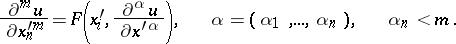 | (6) |
Cauchy problems are usually studied when the carrier of the initial data is a non-characteristic surface, i.e. when condition (5) holds for all 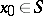 .
.
The Cauchy–Kovalevskaya theorem occupies an important position in the theory of Cauchy problems; it runs as follows. If 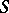 is an analytic surface in a neighbourhood of one of its points
is an analytic surface in a neighbourhood of one of its points  , if the functions
, if the functions  ,
, 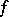 and
and 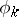 ,
, 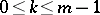 , are analytic in the same neighbourhood, and if moreover condition (5) is satisfied, then the Cauchy problem (3), (4) has an analytic solution
, are analytic in the same neighbourhood, and if moreover condition (5) is satisfied, then the Cauchy problem (3), (4) has an analytic solution 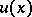 in a neighbourhood of the point; this solution is unique in the class of analytic functions. With the analyticity assumption, this theorem is also valid for general non-linear equations if the latter can be reduced to the normal form (6), and also for systems of such equations. The theorem is universal in nature, since it is applicable to analytic equations regardless of their type (elliptic, hyperbolic, etc.) and yields the local existence of a solution. The solution is unique in the class of non-analytic functions.
in a neighbourhood of the point; this solution is unique in the class of analytic functions. With the analyticity assumption, this theorem is also valid for general non-linear equations if the latter can be reduced to the normal form (6), and also for systems of such equations. The theorem is universal in nature, since it is applicable to analytic equations regardless of their type (elliptic, hyperbolic, etc.) and yields the local existence of a solution. The solution is unique in the class of non-analytic functions.
The Cauchy problem for partial differential equations of order exceeding 1 may turn out to be ill-posed if one drops the analyticity assumption for the equation or for the Cauchy data in the Cauchy–Kovalevskaya theorem. An illustration is Hadamard's example: The Cauchy problem for the Laplace equation
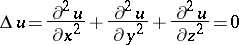 |
with initial conditions
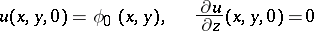 |
has no solution if 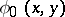 is not an analytic function.
is not an analytic function.
The hyperbolic equations constitute a broad class of equations for which the Cauchy problem is well-posed. In this case the Cauchy problem is global in nature, but the condition that  be non-characteristic is no longer sufficient. It is necessary that
be non-characteristic is no longer sufficient. It is necessary that  is a space-like surface. A typical hyperbolic equation is the wave equation
is a space-like surface. A typical hyperbolic equation is the wave equation
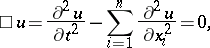 | (7) |
considered in an 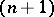 -dimensional region, with variables
-dimensional region, with variables 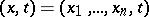 . The Cauchy problem for this equation with data
. The Cauchy problem for this equation with data
 |
on the hyperplane 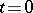 is uniquely solvable for any sufficiently smooth functions
is uniquely solvable for any sufficiently smooth functions 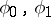 , and the solution depends continuously (in some
, and the solution depends continuously (in some 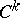 metric) on these functions. For the cases
metric) on these functions. For the cases 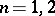 and
and 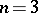 , an explicit form of the solution is given by the formulas of d'Alembert, Poisson and Kirchhoff, respectively:
, an explicit form of the solution is given by the formulas of d'Alembert, Poisson and Kirchhoff, respectively:
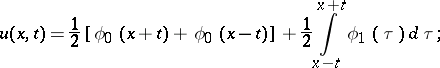 |
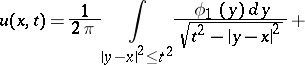 |
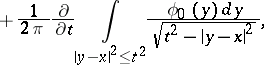 |
where 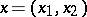 ,
, 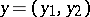 ;
;
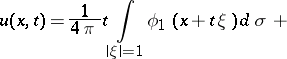 |
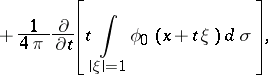 |
where 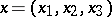 ,
, 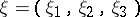 , and
, and  is the surface element on the unit sphere
is the surface element on the unit sphere 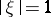 .
.
The set of points in the plane 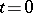 for which the Cauchy data completely determine the value
for which the Cauchy data completely determine the value 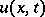 of the solution of the wave equation (7) at a point
of the solution of the wave equation (7) at a point 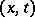 is called the domain of dependence of the latter point. The domains of dependence of the point
is called the domain of dependence of the latter point. The domains of dependence of the point 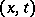 in the cases
in the cases 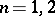 and
and 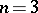 are, respectively, the closed interval, disc and ball defined by
are, respectively, the closed interval, disc and ball defined by 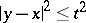 (in the appropriate space
(in the appropriate space 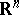 ). If the carrier of the Cauchy data is some region
). If the carrier of the Cauchy data is some region 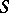 on the hyperplane
on the hyperplane 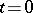 , then the Cauchy data in that region affect the solution at all points
, then the Cauchy data in that region affect the solution at all points 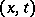 of the set such that the intersection
of the set such that the intersection 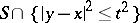 is not empty; this set is known as the domain of influence.
is not empty; this set is known as the domain of influence.
The set of points 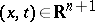 at which the solution
at which the solution  is completely determined by the Cauchy data on
is completely determined by the Cauchy data on 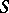 is called the domain of definition of
is called the domain of definition of 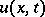 with initial data on
with initial data on 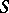 . In cases
. In cases 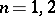 and 3 the domain of definition consists of all points
and 3 the domain of definition consists of all points 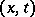 for which the closed interval, disc or ball,
for which the closed interval, disc or ball, 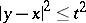 (as the case may be), lies in
(as the case may be), lies in 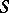 .
.
These results carry over to the more general case in which the carrier of the Cauchy data is a surface 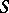 of spatial type, i.e. a surface for which
of spatial type, i.e. a surface for which 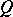 (see (5)) remains positive on
(see (5)) remains positive on 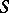 .
.
There are other problems besides the Cauchy problem which prove to be well-posed for hyperbolic equations; examples are the Cauchy characteristic problem and mixed initial-boundary value problems. In the latter type of problem, a solution exists in an 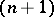 -dimensional cylinder with generatrix parallel to the
-dimensional cylinder with generatrix parallel to the 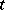 -axis and a base
-axis and a base  which is some region in the space of variables
which is some region in the space of variables 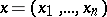 with boundary
with boundary 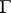 . The carrier of the initial conditions is
. The carrier of the initial conditions is 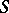 , while the value of the function, its normal derivative (in the case of second-order equations), or more general boundary value conditions, are given on the lateral surface
, while the value of the function, its normal derivative (in the case of second-order equations), or more general boundary value conditions, are given on the lateral surface  of the cylinder.
of the cylinder.
In the case of degenerate equations the formulation of the Cauchy problem also has to be modified. For example, if the equation is of hyperbolic type and the carrier of the Cauchy data is a surface on which the equation becomes parabolically degenerate, then, depending on the nature of degeneracy, the initial value conditions may involve the use of some weight function.
References
| [1] | S. Kovalevskaya, "Scientific works" , Moscow (1948) (In Russian) |
| [2] | J. Hadamard, "Lectures on Cauchy's problem in linear partial differential equations" , Dover, reprint (1952) (Translated from French) |
| [3] | L. Bers, F. John, M. Schechter, "Partial differential equations" , Interscience (1964) |
| [4] | A.V. Bitsadze, "Equations of mathematical physics" , MIR (1980) (Translated from Russian) |
| [5] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) |
| [6] | S. Mizohata, "The theory of partial differential equations" , Cambridge Univ. Press (1973) (Translated from Japanese) |
| [7] | A.N. [A.N. Tikhonov] Tichonoff, A.A. Samarskii, "Differentialgleichungen der mathematischen Physik" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [8] | L. Hörmander, "Linear partial differential operators" , Springer (1964) |
Comments
The name "Cauchy problem" is mostly used in relation with hyperbolic initial value problems. Hörmander [8] has been followed by 4 volumes. Two of them [a2] deal with Cauchy problems.
It is clear from the Kirchhoff solution 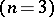 of (7) that the domain of dependence of the point
of (7) that the domain of dependence of the point 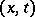 is, in fact, the sphere
is, in fact, the sphere 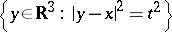 . The relevance of this remark for the general definition of domain of dependence for hyperbolic partial differential equations is discussed in [5], Sect. VI.7.
. The relevance of this remark for the general definition of domain of dependence for hyperbolic partial differential equations is discussed in [5], Sect. VI.7.
It is modern practice to define hyperbolicity of a partial differential operator as a necessary condition for the well-posedness of the Cauchy problem, see [a2], Vol. 2, Sect. 12.3.
References
| [a1] | P.R. Garabedian, "Partial differential equations" , Wiley (1964) |
| [a2] | L.V. Hörmander, "The analysis of linear partial differential operators" , 1–2 , Springer (1985) |
| [a3] | F. Treves, "Basic partial differential equations" , Acad. Press (1975) |
Cauchy problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cauchy_problem&oldid=14181