Cauchy criteria
The Cauchy criterion on the convergence of a sequence of numbers: A sequence of (real or complex) numbers 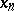 ,
, 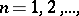 converges to a limit if and only if, given
converges to a limit if and only if, given 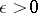 , there exists an
, there exists an 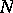 such that, for all
such that, for all 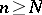 and
and 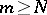 ,
,
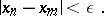 |
The Cauchy criterion on the convergence of a sequence of numbers may be generalized to a criterion on the convergence of points in a complete metric space.
A sequence of points  of a complete metric space is convergent if and only if, given
of a complete metric space is convergent if and only if, given 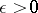 , there exists an
, there exists an 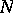 such that, for all
such that, for all 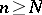 and
and 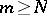 , the inequality
, the inequality 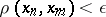 holds.
holds.
The Cauchy criterion on the existence of a limit of a function of  variables
variables 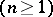 . Let
. Let 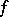 be a function defined on a set
be a function defined on a set 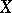 in an
in an  -dimensional space
-dimensional space 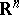 , taking real or complex values, and let
, taking real or complex values, and let  be a limit point of the set
be a limit point of the set 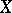 (or the symbol
(or the symbol 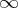 , in which case the set
, in which case the set 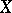 is unbounded). There exists a finite limit
is unbounded). There exists a finite limit 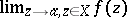 if and only if, given
if and only if, given 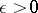 , there exists a neighbourhood
, there exists a neighbourhood 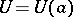 of
of  such that, for any
such that, for any 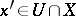 and
and 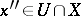 ,
,
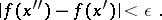 |
This criterion may be generalized to more general mappings: Let 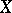 be a topological space,
be a topological space,  a limit point of
a limit point of 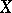 at which the first axiom of countability is valid,
at which the first axiom of countability is valid, 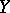 a complete metric space, and
a complete metric space, and 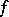 a mapping of
a mapping of 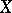 into
into 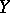 . Then the limit
. Then the limit
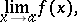 |
exists if and only if, given 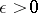 , there exists a neighbourhood
, there exists a neighbourhood 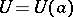 of
of  such that, for all
such that, for all 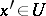 and
and 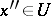 ,
,
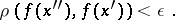 |
The Cauchy criterion on the uniform convergence of a family of functions. Let 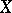 be a set,
be a set, 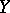 a topological space with a limit point
a topological space with a limit point 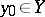 at which the first axiom of countability holds,
at which the first axiom of countability holds,  a complete metric space,
a complete metric space, 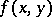 a mapping of the set
a mapping of the set 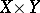 into
into 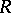 ,
, 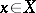 ,
, 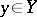 . Then the family of functions
. Then the family of functions 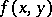 mapping, for a fixed
mapping, for a fixed 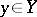 ,
, 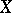 into
into 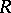 is uniformly convergent on
is uniformly convergent on  as
as 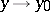 if, given
if, given 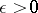 , there exists a neighbourhood
, there exists a neighbourhood 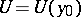 of
of 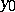 such that, for all
such that, for all 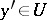 ,
, 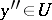 and all
and all 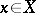 ,
,
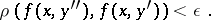 |
In particular, if 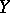 is the set of natural numbers and
is the set of natural numbers and 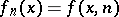 , then the sequence
, then the sequence  is uniformly convergent on
is uniformly convergent on 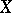 as
as 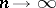 if and only if, given
if and only if, given 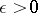 , there exists an
, there exists an 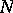 such that, for all
such that, for all  and all
and all 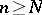 ,
, 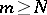 ,
,
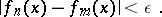 |
The Cauchy criterion on the convergence of a series: A series of real numbers  is convergent if and only if, given
is convergent if and only if, given  , there exists an
, there exists an  such that, for all
such that, for all 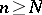 and all integers
and all integers 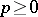 ,
,
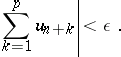 |
The analogue of this criterion for multiple series is known as the Cauchy–Stolz criterion. For example, a double series
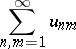 |
is convergent in the sense of convergence of rectangular partial sums
 |
if and only if, given 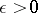 , there exists an
, there exists an 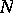 such that, for all
such that, for all 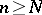 ,
, 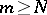 and all integers
and all integers 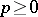 ,
, 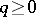 ,
,
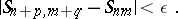 |
These criteria generalize to series in Banach spaces (with absolute values replaced by the appropriate norms of the elements).
The Cauchy criterion on the uniform convergence of a series: Let 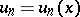 ,
, 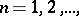 be functions defined on some set
be functions defined on some set 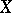 and taking real values. The series
and taking real values. The series
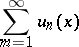 |
is uniformly convergent on 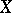 if and only if, given
if and only if, given 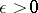 , there exists an
, there exists an 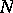 such that, for all
such that, for all 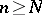 , all integers
, all integers 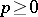 and all
and all 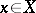 ,
,
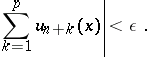 |
This criterion also carries over to multiple series, and moreover not only with numerical terms but also with terms in Banach spaces, i.e. to series in which the 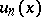 are mappings of
are mappings of 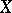 into a Banach space.
into a Banach space.
The Cauchy criterion on the convergence of improper integrals: Let 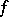 be a function defined on a half-closed interval
be a function defined on a half-closed interval 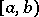 ,
, 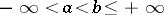 , taking numerical values. Suppose that for any
, taking numerical values. Suppose that for any 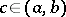 the function
the function 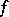 is (Riemann- or Lebesgue-) integrable on
is (Riemann- or Lebesgue-) integrable on 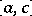 . Then the improper integral
. Then the improper integral
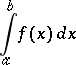 |
is convergent if and only if, given  , there exists an
, there exists an 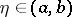 such that, for all
such that, for all 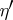 and
and 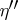 satisfying the condition
satisfying the condition 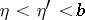 ,
, 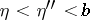 ,
,
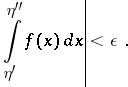 |
The criterion can be formulated in an analogous way for improper integrals of other types, and it also generalizes to the case in which 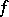 depends on several variables and assumes values in a Banach space.
depends on several variables and assumes values in a Banach space.
The Cauchy criterion on the uniform convergence of improper integrals: Let 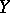 be some set and suppose that, for every fixed
be some set and suppose that, for every fixed 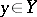 , the function
, the function 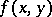 is defined on a half-closed interval
is defined on a half-closed interval 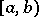 ,
, 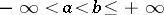 , and takes numerical values. Suppose that for any
, and takes numerical values. Suppose that for any  the function
the function 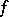 is integrable with respect to
is integrable with respect to  on
on 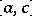 . Then the integral
. Then the integral
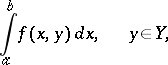 |
is uniformly convergent on 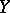 if and only if, given any
if and only if, given any  , there exists an
, there exists an 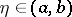 such that, for any
such that, for any 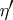 and
and 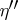 satisfying the conditions
satisfying the conditions 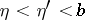 ,
, 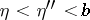 , and all
, and all 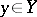 ,
,
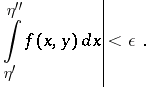 |
This criterion also carries over to improper integrals of other types, to functions of several variables and to functions taking values in Banach spaces.
References
| [1] | A.L. Cauchy, "Analyse algébrique" , Gauthier-Villars (1821) (German translation: Springer, 1885) |
| [2] | O. Stolz, Math. Ann. , 24 (1884) pp. 154–171 |
| [3] | J.A. Dieudonné, "Foundations of modern analysis" , Acad. Press (1961) (Translated from French) |
| [4] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1971–1973) (Translated from Russian) |
| [5] | L.D. Kudryavtsev, "A course in mathematical analysis" , 1–2 , Moscow (1981) (In Russian) |
| [6] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian) |
| [7] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) pp. Chapt. 6 |
Comments
The criterion in 1) can be reformulated as: A sequence of numbers is convergent if and only if it is a Cauchy sequence (see also [a1]). This property of sequences of elements of a metric space is often taken as a definition of completeness of the latter: A metric space is called complete if every Cauchy sequence in it converges.
References
| [a1] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1976) |
Cauchy criteria. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cauchy_criteria&oldid=15239