Cauchy Schwarz inequality
The Cauchy inequality for finite sums of real numbers is the inequality
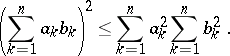 |
Proved by A.L. Cauchy (1821); the analogue for integrals is known as the Bunyakovskii inequality.
The Cauchy inequality is also the name used for an inequality for the modulus  of a derivative of a regular analytic function
of a derivative of a regular analytic function  at a fixed point
at a fixed point  of the complex plane
of the complex plane  , or for the modulus
, or for the modulus  of the coefficients of the power series expansion of
of the coefficients of the power series expansion of  ,
,
 |
These inequalities are
 | (*) |
where  is the radius of any disc
is the radius of any disc 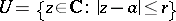 on which
on which 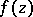 is regular, and
is regular, and  is the maximum modulus of
is the maximum modulus of 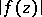 on the circle
on the circle  . The inequalities (*) occur in the work of A.L. Cauchy (see e.g. ). They directly imply the Cauchy–Hadamard inequality (see ):
. The inequalities (*) occur in the work of A.L. Cauchy (see e.g. ). They directly imply the Cauchy–Hadamard inequality (see ):
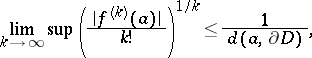 |
where 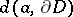 is the distance from
is the distance from  to the boundary
to the boundary 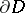 of the domain of holomorphy of
of the domain of holomorphy of  . In particular, if
. In particular, if  is an entire function, then at any point
is an entire function, then at any point  ,
,
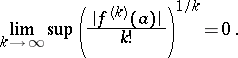 |
For a holomorphic function 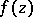 of several complex variables
of several complex variables 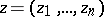 ,
, 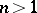 , the Cauchy inequalities are
, the Cauchy inequalities are
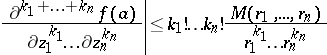 |
or
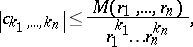 |
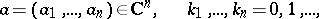 |
where  are the coefficients of the power series expansion of
are the coefficients of the power series expansion of 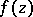 :
:
 |
 are the radii of a polydisc
are the radii of a polydisc 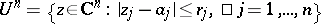 on which
on which  is holomorphic, and
is holomorphic, and 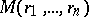 is the maximum of
is the maximum of 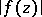 on the distinguished boundary of
on the distinguished boundary of  .
.
For references see Cauchy–Hadamard theorem.
Comments
In Western literature the name Bunyakovskii inequality is rarely used. Both the inequality for finite sums of real numbers, or its generalization to complex numbers (see Bunyakovskii inequality), and its analogue for integrals are often called the Schwarz inequality or the Cauchy–Schwarz inequality.
The distinguished boundary of a polydisc 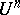 as above is the set
as above is the set  .
.
Cauchy Schwarz inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cauchy_Schwarz_inequality&oldid=12979