Difference between revisions of "Category with involution"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | c0207801.png | ||
| + | $#A+1 = 18 n = 1 | ||
| + | $#C+1 = 18 : ~/encyclopedia/old_files/data/C020/C.0200780 Category with involution | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A category possessing a number of characteristic properties of the category of binary relations. A category with involution is a category in which every set $ H ( A , B ) $ | |
| + | is partially ordered by the relation $ \subset $; | ||
| + | also, a mapping is prescribed, the so-called involution, which associates with each morphism $ \alpha $ | ||
| + | a morphism $ \alpha ^ {\#} $ | ||
| + | satisfying the following conditions: | ||
| − | + | a) if $ \alpha \in H ( A , B ) $, | |
| + | then $ \alpha ^ {\#} \in H ( B , A ) $; | ||
| − | + | b) $ \alpha ^ {\#\#} = \alpha $; | |
| + | |||
| + | c) if $ \alpha \in H ( A , B ) $, | ||
| + | $ \beta \in H ( B , C ) $, | ||
| + | then $ ( \alpha \beta ) ^ {\#} = \beta ^ {\#} \alpha ^ {\#} $; | ||
| + | |||
| + | d) if $ \alpha \subset \beta $, | ||
| + | $ \alpha , \beta \in H ( A , B ) $ | ||
| + | and $ \gamma \in H ( B , C ) $, | ||
| + | then $ \alpha \gamma \subset \beta \gamma $. | ||
In a category with involution, statements dual to true statements are also true (the strong duality principle). The dual of a category with involution is a category with involution. Every group can be regarded as a category with involution, consisting of a single object for which the order relation is the identity relation (the trivial partial ordering), and the involution is the mapping which associates with each element of the group its inverse. | In a category with involution, statements dual to true statements are also true (the strong duality principle). The dual of a category with involution is a category with involution. Every group can be regarded as a category with involution, consisting of a single object for which the order relation is the identity relation (the trivial partial ordering), and the involution is the mapping which associates with each element of the group its inverse. | ||
| − | An important example of a category with involution is the category of binary relations | + | An important example of a category with involution is the category of binary relations $ \mathfrak R ( \mathfrak S ) $ |
| + | over the category of sets $ \mathfrak S $, | ||
| + | constructed in the following way. $ \mathop{\rm Ob} \mathfrak R ( \mathfrak S ) = \mathop{\rm Ob} \mathfrak S $, | ||
| + | the morphisms of $ \mathfrak R ( \mathfrak S ) $ | ||
| + | are the binary relations with the usual product and the partial order induced by the inclusion relation of subsets of the Cartesian product. The involution in this category is defined by interchange of the factors in the Cartesian product. In a similar fashion, the categories of binary relations can be constructed over the categories of groups, rings, topological groups, etc. However, for the category of topological spaces the construction above depends on the choice of a bicategory structure and can lead to a non-associative product. | ||
A description of the construction of various classes of categories with involution, their connection with the classes of exact, Abelian and regular categories, and their use in homological algebra can be found in [[#References|[1]]]–[[#References|[4]]]. | A description of the construction of various classes of categories with involution, their connection with the classes of exact, Abelian and regular categories, and their use in homological algebra can be found in [[#References|[1]]]–[[#References|[4]]]. | ||
Revision as of 15:35, 4 June 2020
A category possessing a number of characteristic properties of the category of binary relations. A category with involution is a category in which every set $ H ( A , B ) $
is partially ordered by the relation $ \subset $;
also, a mapping is prescribed, the so-called involution, which associates with each morphism $ \alpha $
a morphism $ \alpha ^ {\#} $
satisfying the following conditions:
a) if $ \alpha \in H ( A , B ) $, then $ \alpha ^ {\#} \in H ( B , A ) $;
b) $ \alpha ^ {\#\#} = \alpha $;
c) if $ \alpha \in H ( A , B ) $, $ \beta \in H ( B , C ) $, then $ ( \alpha \beta ) ^ {\#} = \beta ^ {\#} \alpha ^ {\#} $;
d) if $ \alpha \subset \beta $, $ \alpha , \beta \in H ( A , B ) $ and $ \gamma \in H ( B , C ) $, then $ \alpha \gamma \subset \beta \gamma $.
In a category with involution, statements dual to true statements are also true (the strong duality principle). The dual of a category with involution is a category with involution. Every group can be regarded as a category with involution, consisting of a single object for which the order relation is the identity relation (the trivial partial ordering), and the involution is the mapping which associates with each element of the group its inverse.
An important example of a category with involution is the category of binary relations $ \mathfrak R ( \mathfrak S ) $ over the category of sets $ \mathfrak S $, constructed in the following way. $ \mathop{\rm Ob} \mathfrak R ( \mathfrak S ) = \mathop{\rm Ob} \mathfrak S $, the morphisms of $ \mathfrak R ( \mathfrak S ) $ are the binary relations with the usual product and the partial order induced by the inclusion relation of subsets of the Cartesian product. The involution in this category is defined by interchange of the factors in the Cartesian product. In a similar fashion, the categories of binary relations can be constructed over the categories of groups, rings, topological groups, etc. However, for the category of topological spaces the construction above depends on the choice of a bicategory structure and can lead to a non-associative product.
A description of the construction of various classes of categories with involution, their connection with the classes of exact, Abelian and regular categories, and their use in homological algebra can be found in [1]–[4].
References
| [1] | H.B. Brinkmann, D. Puppe, "Abelsche und exakte Kategorien" , Springer (1969) |
| [2] | J. Kawahara, "Relations in categories with pullbacks" Mem. Fac. Sci. Kyushu Univ. Ser. A. Math. , 27 : 1 (1973) pp. 149–173 |
| [3] | J. Kawahara, "Matrix calculus in 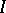 -categories and an axiomatic characterization of relations in a regular category" Mem. Fac. Sci. Kyushu Univ. Ser. A. Math. , 27 : 2 (1973) pp. 249–273 -categories and an axiomatic characterization of relations in a regular category" Mem. Fac. Sci. Kyushu Univ. Ser. A. Math. , 27 : 2 (1973) pp. 249–273 |
| [4] | M.Sh. Tsalenko, "Correspondence categories over regular categories" Soviet Math. Doklady , 14 (1973) pp. 1026–1029 Dokl. Akad. Nauk SSSR , 211 : 2 (1973) pp. 297–299 |
Category with involution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Category_with_involution&oldid=16991