Carson transform
From Encyclopedia of Mathematics
The result of transformation of a function 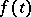 defined for
defined for 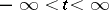 and vanishing when
and vanishing when 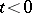 , into the function
, into the function
 |
where  is a complex variable. The inversion formula is
is a complex variable. The inversion formula is
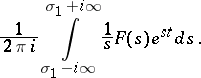 |
The difference between the Carson transform of 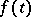 and its Laplace transform is the presence of the factor
and its Laplace transform is the presence of the factor  .
.
Comments
Two well-known references for the Laplace transformation are [a1], which stresses the theory, and [a2], which stresses applications.
References
| [a1] | D.V. Widder, "The Laplace transform" , Princeton Univ. Press (1972) |
| [a2] | G. Doetsch, "Introduction to the theory and application of the Laplace transformation" , Springer (1974) (Translated from German) |
How to Cite This Entry:
Carson transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carson_transform&oldid=17141
Carson transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carson_transform&oldid=17141
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article