C*-algebra
A Banach algebra 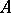 over the field of complex numbers, with an involution
over the field of complex numbers, with an involution 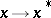 ,
, 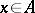 , such that the norm and the involution are connected by the relation
, such that the norm and the involution are connected by the relation 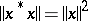 for any element
for any element 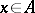 .
. 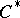 -algebras were introduced in 1943 [1] under the name of totally regular rings; they are also known under the name of
-algebras were introduced in 1943 [1] under the name of totally regular rings; they are also known under the name of 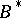 -algebras. The most important examples of
-algebras. The most important examples of 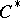 -algebras are:
-algebras are:
1) The algebra 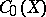 of continuous complex-valued functions on a locally compact Hausdorff space
of continuous complex-valued functions on a locally compact Hausdorff space 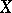 which tend towards zero at infinity (i.e. continuous functions
which tend towards zero at infinity (i.e. continuous functions  on
on 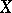 such that, for any
such that, for any 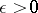 , the set of points
, the set of points 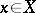 which satisfy the condition
which satisfy the condition 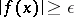 is compact in
is compact in 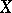 );
); 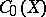 has the uniform norm
has the uniform norm
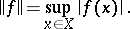 |
The involution in 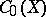 is defined as transition to the complex-conjugate function:
is defined as transition to the complex-conjugate function: 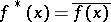 . Any commutative
. Any commutative  -algebra
-algebra 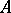 is isometrically and symmetrically isomorphic (i.e. is isomorphic as a Banach algebra
is isometrically and symmetrically isomorphic (i.e. is isomorphic as a Banach algebra 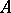 with involution) to the
with involution) to the  -algebra
-algebra 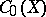 , where
, where 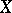 is the space of maximal ideals of
is the space of maximal ideals of 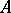 endowed with the Gel'fand topology [1], [2], [3].
endowed with the Gel'fand topology [1], [2], [3].
2) The algebra 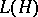 of all bounded linear operators on a Hilbert space
of all bounded linear operators on a Hilbert space 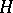 , considered with respect to the ordinary linear operations and operator multiplication. The involution in
, considered with respect to the ordinary linear operations and operator multiplication. The involution in 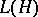 is defined as transition to the adjoint operator, and the norm is defined as the ordinary operator norm.
is defined as transition to the adjoint operator, and the norm is defined as the ordinary operator norm.
A subset 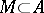 is said to be self-adjoint if
is said to be self-adjoint if 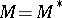 , where
, where 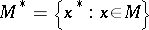 . Any closed self-adjoint subalgebra
. Any closed self-adjoint subalgebra 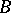 of a
of a 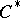 -algebra
-algebra 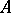 is a
is a 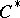 -algebra with respect to the linear operations, multiplication, involution, and norm taken from
-algebra with respect to the linear operations, multiplication, involution, and norm taken from  ;
;  is said to be a
is said to be a 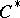 -subalgebra of
-subalgebra of 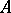 . Any
. Any 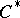 -algebra is isometrically and symmetrically isomorphic to a
-algebra is isometrically and symmetrically isomorphic to a 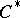 -subalgebra of some
-subalgebra of some 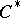 -algebra of the form
-algebra of the form 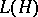 . Any closed two-sided ideal
. Any closed two-sided ideal  in a
in a  -algebra is self-adjoint (thus
-algebra is self-adjoint (thus 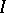 is a
is a 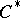 -subalgebra of
-subalgebra of 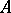 ), and the quotient algebra
), and the quotient algebra 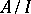 , endowed with the natural linear operations, multiplication, involution, and quotient space norm, is a
, endowed with the natural linear operations, multiplication, involution, and quotient space norm, is a 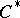 -algebra. The set
-algebra. The set 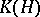 of completely-continuous linear operators on a Hilbert space
of completely-continuous linear operators on a Hilbert space 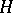 is a closed two-sided ideal in
is a closed two-sided ideal in 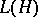 . If
. If 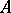 is a
is a 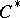 -algebra and
-algebra and 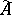 is the algebra with involution obtained from
is the algebra with involution obtained from 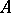 by addition of a unit element, there exists a unique norm on
by addition of a unit element, there exists a unique norm on 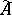 which converts
which converts 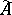 into a
into a 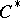 -algebra and which extends the norm on
-algebra and which extends the norm on 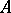 . Moreover, the operations of bounded direct sum and tensor product [3], [4] have been defined for
. Moreover, the operations of bounded direct sum and tensor product [3], [4] have been defined for 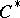 -algebras.
-algebras.
As in all symmetric Banach algebras with involution, in a 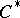 -algebra
-algebra 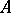 it is possible to define the following subsets: the real linear space
it is possible to define the following subsets: the real linear space 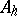 of Hermitian elements; the set of normal elements; the multiplicative group
of Hermitian elements; the set of normal elements; the multiplicative group 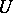 of unitary elements (if
of unitary elements (if 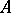 contains a unit element); and the set
contains a unit element); and the set 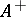 of positive elements. The set
of positive elements. The set 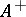 is a closed cone in
is a closed cone in 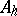 ,
, 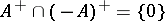 ,
,  , and the cone
, and the cone 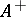 converts
converts 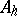 into a real ordered vector space. If
into a real ordered vector space. If 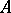 contains a unit element 1, then 1 is an interior point of the cone
contains a unit element 1, then 1 is an interior point of the cone 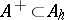 . A linear functional
. A linear functional  on
on 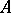 is called positive if
is called positive if 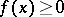 for all
for all 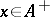 ; such a functional is continuous. If
; such a functional is continuous. If 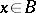 , where
, where 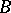 is a
is a 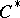 -subalgebra of
-subalgebra of 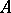 , the spectrum of
, the spectrum of  in
in 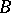 coincides with the spectrum of
coincides with the spectrum of  in
in 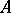 . The spectrum of a Hermitian element is real, the spectrum of a unitary element lies on the unit circle, and the spectrum of a positive element is non-negative. A functional calculus for the normal elements of a
. The spectrum of a Hermitian element is real, the spectrum of a unitary element lies on the unit circle, and the spectrum of a positive element is non-negative. A functional calculus for the normal elements of a 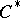 -algebra has been constructed. Any
-algebra has been constructed. Any 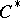 -algebra
-algebra 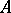 has an approximate unit, located in the unit ball of
has an approximate unit, located in the unit ball of 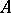 and formed by positive elements of
and formed by positive elements of 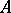 . If
. If 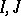 are closed two-sided ideals in
are closed two-sided ideals in 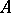 , then
, then 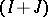 is a closed two-sided ideal in
is a closed two-sided ideal in 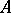 and
and 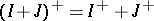 . If
. If  is a closed two-sided ideal in
is a closed two-sided ideal in  and
and 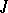 is a closed two-sided ideal in
is a closed two-sided ideal in 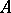 , then
, then 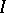 is a closed two-sided ideal in
is a closed two-sided ideal in 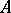 . Any closed two-sided ideal is the intersection of the primitive two-sided ideals in which it is contained; any closed left ideal in
. Any closed two-sided ideal is the intersection of the primitive two-sided ideals in which it is contained; any closed left ideal in 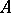 is the intersection of the maximal regular left ideals in which it is contained.
is the intersection of the maximal regular left ideals in which it is contained.
Any *-isomorphism of a  -algebra is isometric. Any *-isomorphism
-algebra is isometric. Any *-isomorphism 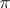 of a Banach algebra
of a Banach algebra 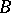 with involution into a
with involution into a 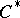 -algebra
-algebra 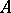 is continuous, and
is continuous, and 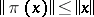 for all
for all 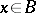 . In particular, all representations of a Banach algebra with involution (i.e. all *-homomorphism of
. In particular, all representations of a Banach algebra with involution (i.e. all *-homomorphism of 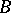 into a
into a 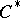 -algebra of the form
-algebra of the form 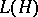 ) are continuous. The theory of representations of
) are continuous. The theory of representations of 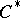 -algebras forms a significant part of the theory of
-algebras forms a significant part of the theory of 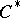 -algebras, and the applications of the theory of
-algebras, and the applications of the theory of 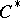 -algebras are related to the theory of representations of
-algebras are related to the theory of representations of 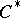 -algebras. The properties of representations of
-algebras. The properties of representations of 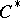 -algebras make it possible to construct for each
-algebras make it possible to construct for each 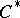 -algebra
-algebra 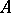 a topological space
a topological space 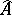 , called the spectrum of the
, called the spectrum of the  -algebra
-algebra  , and to endow this space with a Mackey–Borel structure. In the general case, the spectrum of a
, and to endow this space with a Mackey–Borel structure. In the general case, the spectrum of a  -algebra does not satisfy any separation axiom, but is a locally compact Baire space.
-algebra does not satisfy any separation axiom, but is a locally compact Baire space.
A 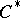 -algebra
-algebra 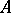 is said to be a CCR-algebra (respectively, a GCR-algebra) if the relation
is said to be a CCR-algebra (respectively, a GCR-algebra) if the relation 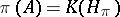 (respectively,
(respectively, 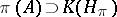 ) is satisfied for any non-null irreducible representation
) is satisfied for any non-null irreducible representation 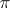 of the
of the 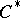 -algebra
-algebra 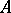 in a Hilbert space
in a Hilbert space 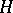 .
.
A  -algebra
-algebra 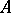 is said to be an NGCR-algebra if
is said to be an NGCR-algebra if 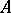 does not contain non-zero closed two-sided
does not contain non-zero closed two-sided 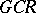 -ideals (i.e. ideals which are
-ideals (i.e. ideals which are 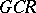 -algebras). Any
-algebras). Any 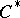 -algebra contains a maximal two-sided
-algebra contains a maximal two-sided 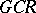 -ideal
-ideal 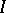 , and the quotient algebra
, and the quotient algebra 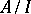 is an
is an 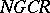 -algebra. Any
-algebra. Any 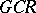 -algebra contains an increasing family of closed two-sided ideals
-algebra contains an increasing family of closed two-sided ideals 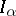 , indexed by ordinals
, indexed by ordinals 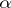 ,
, 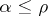 , such that
, such that 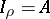 ,
, 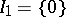 ,
, 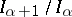 is a
is a  -algebra for all
-algebra for all 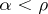 , and
, and 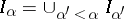 for limit ordinals
for limit ordinals 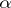 . The spectrum of a
. The spectrum of a 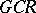 -algebra contains an open, everywhere-dense, separable, locally compact subset.
-algebra contains an open, everywhere-dense, separable, locally compact subset.
A 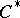 -algebra
-algebra 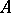 is said to be a
is said to be a 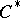 -algebra of type I if, for any representation
-algebra of type I if, for any representation 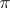 of the
of the 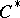 -algebra
-algebra 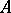 in a Hilbert space
in a Hilbert space 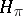 , the von Neumann algebra generated by the family
, the von Neumann algebra generated by the family 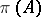 in
in 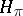 is a type I von Neumann algebra. For a
is a type I von Neumann algebra. For a 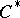 -algebra, the following conditions are equivalent: a)
-algebra, the following conditions are equivalent: a) 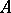 is a
is a 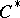 -algebra of type I; b)
-algebra of type I; b) 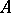 is a
is a 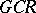 -algebra; and c) any quotient representation of the
-algebra; and c) any quotient representation of the 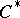 -algebra
-algebra 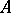 is a multiple of the irreducible representation. If
is a multiple of the irreducible representation. If 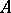 satisfies these conditions, then: 1) two irreducible representations of the
satisfies these conditions, then: 1) two irreducible representations of the 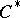 -algebra
-algebra 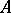 are equivalent if and only if their kernels are identical; and 2) the spectrum of the
are equivalent if and only if their kernels are identical; and 2) the spectrum of the 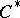 -algebra
-algebra 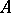 is a
is a 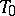 -space. If
-space. If 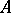 is a separable
is a separable 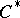 -algebra, each of the conditions 1) and 2) is equivalent to the conditions a)–c). In particular, each separable
-algebra, each of the conditions 1) and 2) is equivalent to the conditions a)–c). In particular, each separable 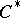 -algebra with a unique (up to equivalence) irreducible representation, is isomorphic to the
-algebra with a unique (up to equivalence) irreducible representation, is isomorphic to the 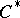 -algebra
-algebra 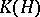 for some Hilbert space
for some Hilbert space 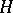 .
.
Let 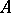 be a
be a 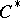 -algebra, and let
-algebra, and let 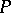 be a set of elements
be a set of elements 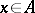 such that the function
such that the function 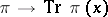 is finite and continuous on the spectrum of
is finite and continuous on the spectrum of 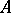 . If the linear envelope of
. If the linear envelope of 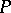 is everywhere dense in
is everywhere dense in 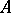 , then
, then 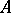 is said to be a
is said to be a 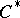 -algebra with continuous trace. The spectrum of such a
-algebra with continuous trace. The spectrum of such a 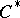 -algebra is separable and, under certain additional conditions, a
-algebra is separable and, under certain additional conditions, a 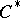 -algebra with a continuous trace may be represented as the algebra of vector functions on its spectrum
-algebra with a continuous trace may be represented as the algebra of vector functions on its spectrum 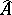 [3].
[3].
Let 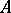 be a
be a 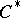 -algebra, let
-algebra, let 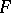 be the set of positive linear functionals on
be the set of positive linear functionals on 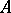 with norm
with norm 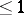 and let
and let 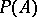 be the set of non-zero boundary points of the convex set
be the set of non-zero boundary points of the convex set 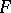 . Then
. Then 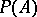 will be the set of pure states of
will be the set of pure states of 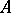 . Let
. Let 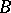 be a
be a 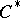 -subalgebra of
-subalgebra of 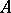 . If
. If 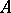 is a
is a  -algebra and if
-algebra and if 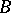 separates the points of the set
separates the points of the set 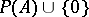 , i.e. for any
, i.e. for any 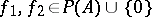 ,
, 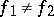 , there exists an
, there exists an  such that
such that 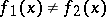 , then
, then 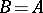 (the Stone–Weierstrass theorem). If
(the Stone–Weierstrass theorem). If 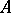 is any
is any 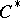 -algebra and
-algebra and 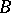 separates the points of the set
separates the points of the set 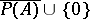 , then
, then 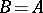 .
.
The second dual space 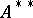 of a
of a 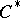 -algebra
-algebra 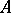 is obviously provided with a multiplication converting
is obviously provided with a multiplication converting 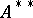 into a
into a 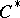 -algebra isomorphic to some von Neumann algebra; this algebra is named the von Neumann algebra enveloping the
-algebra isomorphic to some von Neumann algebra; this algebra is named the von Neumann algebra enveloping the 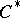 -algebra [3], [4].
-algebra [3], [4].
The theory of 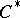 -algebras has numerous applications in the theory of representations of groups and symmetric algebras [3], the theory of dynamical systems [4], statistical physics and quantum field theory [5], and also in the theory of operators on a Hilbert space [6].
-algebras has numerous applications in the theory of representations of groups and symmetric algebras [3], the theory of dynamical systems [4], statistical physics and quantum field theory [5], and also in the theory of operators on a Hilbert space [6].
References
| [1] | I.M. Gel'fand, M.A. [M.A. Naimark] Neumark, "On the imbedding of normed rings in the rings of operators in Hilbert space" Mat. Sb. , 12 (54) : 2 (1943) pp. 197–213 |
| [2] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) |
| [3] | J. Dixmier, " algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
| [4] | S. Sakai, "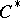 -algebras and -algebras and 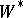 -algebras" , Springer (1971) -algebras" , Springer (1971) |
| [5] | D. Ruelle, "Statistical mechanics: rigorous results" , Benjamin (1974) |
| [6] | R.G. Douglas, "Banach algebra techniques in operator theory" , Acad. Press (1972) |
Comments
If 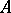 over
over 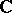 is an algebra with involution, i.e. if there is an operation
is an algebra with involution, i.e. if there is an operation 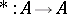 satisfying
satisfying 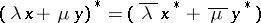 ,
, 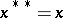 ,
, 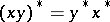 , the Hermitian, normal and positive elements are defined as follows. The element
, the Hermitian, normal and positive elements are defined as follows. The element  is a Hermitian element if
is a Hermitian element if  ; it is a normal element if
; it is a normal element if 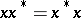 and it is a positive element if
and it is a positive element if  for some
for some 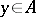 . An element
. An element  is a unitary element if
is a unitary element if 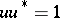 . An algebra with involution is also sometimes called a symmetric algebra (or symmetric ring), cf., e.g., [2]. However, this usage conflicts with the concept of a symmetric algebra as a special kind of Frobenius algebra, cf. Frobenius algebra.
. An algebra with involution is also sometimes called a symmetric algebra (or symmetric ring), cf., e.g., [2]. However, this usage conflicts with the concept of a symmetric algebra as a special kind of Frobenius algebra, cf. Frobenius algebra.
Recent discoveries have revealed connections with, and applications to, algebraic topology. If 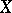 is a compact metrizable space, a group,
is a compact metrizable space, a group, 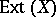 , can be formed from
, can be formed from 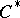 -extensions of the compact operators by
-extensions of the compact operators by 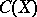 ,
,
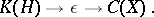 |
In [a3], 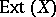 is shown to be a homotopy invariant functor of
is shown to be a homotopy invariant functor of 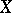 which may be identified with the topological
which may be identified with the topological 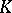 -homology group,
-homology group, 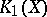 . In [a1] M.F. Atiyah attempted to make a description of
. In [a1] M.F. Atiyah attempted to make a description of 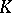 -homology,
-homology, 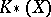 , in terms of elliptic operators [a5], p. 58. In [a7], [a8] G.G. Kasparov developed a solution to this problem. Kasparov and others have used the equivariant version of Kasparov
, in terms of elliptic operators [a5], p. 58. In [a7], [a8] G.G. Kasparov developed a solution to this problem. Kasparov and others have used the equivariant version of Kasparov 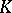 -theory to prove the strong Novikov conjecture on higher signatures in many cases (see [a2], pp. 309-314).
-theory to prove the strong Novikov conjecture on higher signatures in many cases (see [a2], pp. 309-314).
In addition, deep and novel connections between 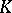 -theory and operator algebras (cf. Operator ring) were recently discovered by A. Connes [a4]. Finally, V.F.R. Jones [a6] has exploited operator algebras to provide invariants of topological knots (cf. Knot theory).
-theory and operator algebras (cf. Operator ring) were recently discovered by A. Connes [a4]. Finally, V.F.R. Jones [a6] has exploited operator algebras to provide invariants of topological knots (cf. Knot theory).
Further details on recent developments may be found in [a2], [a5].
References
| [a1] | M.F. Atiyah, "Global theory of elliptic operators" , Proc. Internat. Conf. Funct. Anal. Related Topics , Univ. Tokyo Press (1970) |
| [a2] | B. Blackadar, "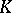 -theory for operator algebras" , Springer (1986) -theory for operator algebras" , Springer (1986) |
| [a3] | L.G. Brown, R.G. Douglas, P.A. Filmore, "Extensions of 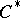 -algebras and -algebras and 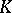 -homology" Ann. of Math. (2) , 105 (1977) pp. 265–324 -homology" Ann. of Math. (2) , 105 (1977) pp. 265–324 |
| [a4] | A. Connes, "Non-commutative differential geometry" Publ. Math. IHES , 62 (1986) pp. 257–360 |
| [a5] | R.G. Douglas, "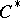 -algebra extensions and -algebra extensions and 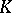 -homology" , Princeton Univ. Press (1980) -homology" , Princeton Univ. Press (1980) |
| [a6] | V.F.R. Jones, "A polynomial invariant for knots via von Neumann algebras" Bull. Amer. Math. Soc. , 12 (1985) pp. 103–111 |
| [a7] | G.G. Kasparov, "The generalized index of elliptic operators" Funct. Anal. and Its Appl. , 7 (1973) pp. 238–240 Funkt. Anal. i Prilozhen. , 7 (1973) pp. 82–83 |
| [a8] | G.G. Kasparov, "Topological invariants of elliptic operators I. 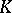 -homology" Math. USSR-Izv. , 9 (1975) pp. 751–792 Izv. Akad. Nauk SSSR , 4 (1975) pp. 796–838 -homology" Math. USSR-Izv. , 9 (1975) pp. 751–792 Izv. Akad. Nauk SSSR , 4 (1975) pp. 796–838 |
| [a9] | M. Takesaki, "Theory of operator algebras" , 1 , Springer (1979) |
C*-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=C*-algebra&oldid=15363