Bredon theory of modules over a category

A module over a small category is a contravariant functor from to the category of -modules, for some commutative ring (cf. also Module). Taking morphisms to be natural transformations, the category of modules over is an Abelian category, so one can do homological algebra with these objects.

G.E. Bredon introduced modules over a category in [a1] in order to study obstruction theory for -spaces. If is a finite group, let be the category of orbits and -mappings between them. -modules (Abelian groups) over play the role of the coefficients in Bredon's (-graded) equivariant ordinary cohomology theories. The equivariant ordinary cohomology of a 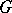-CW-complex can be computed using the equivariant chain complex of the space, which is a chain complex in the category of -modules over . Similarly, equivariant local cohomology can be described using modules over a category depending on the space in question.

For 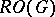-graded equivariant ordinary cohomology one has to replace the orbit category with the stable orbit category, in which the morphisms are the stable mappings between orbits, stabilization being by all representations of . A module over the stable orbit category (i.e., an additive contravariant functor) is equivalent to a Mackey functor as studied by A.W.M. Dress in [a3].

For later examples of the use of modules over a category in equivariant algebraic topology, see [a4] and [a6]. In particular, [a4] includes a discussion of the elementary algebra of modules over a category. For examples involving Mackey functors, see [a2] and [a5].

References

[a1]	G.E. Bredon, "Equivariant cohomology theories" , Lecture Notes Math. , 34 , Springer (1967)
[a2]	T. tom Dieck, "Transformation groups and representation theory" , Lecture Notes Math. , 766 , Springer (1979)
[a3]	A.W.M. Dress, "Contributions to the theory of induced representations" , Algebraic 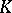-theory, II (Proc. Conf., Battelle Memorial Inst., Seattle, Wash., 1972) , Lecture Notes Math. , 342 , Springer (1973) pp. 183–240
[a4]	W. Lück, "Tranformation groups and algebraic 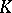-theory" , Lecture Notes Math. , 1408 , Springer (1989)
[a5]	J.P. May, et al., "Equivariant homotopy and cohomology theory" , Regional Conf. Ser. Math. , 91 , Amer. Math. Soc. (1996)
[a6]	I. Moerdijk, J.A. Svensson, "The equivariant Serre spectral sequence" Proc. Amer. Math. Soc. , 118 (1993) pp. 263–278