|
|
| Line 1: |
Line 1: |
| | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, |
| | + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist |
| | + | was used. |
| | + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. |
| | + | |
| | + | Out of 56 formulas, 54 were replaced by TEX code.--> |
| | + | |
| | + | {{TEX|semi-auto}}{{TEX|partial}} |
| | For notation and definitions, see [[Brauer first main theorem|Brauer first main theorem]]. | | For notation and definitions, see [[Brauer first main theorem|Brauer first main theorem]]. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b1204601.png" /> be an element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b1204602.png" /> whose order is a power of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b1204603.png" />. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b1204605.png" />-section of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b1204606.png" /> associated to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b1204607.png" /> is the set of all elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b1204608.png" /> whose <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046010.png" />-part is conjugate to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046011.png" />. Brauer second main theorem relates the values of irreducible characters of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046012.png" /> on the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046013.png" />-section associated to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046014.png" /> to values of characters in certain blocks of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046015.png" />. | + | Let $x$ be an element of $G$ whose order is a power of $p$. The $p$-section of $G$ associated to $x$ is the set of all elements of $G$ whose $p$-part is conjugate to $x$. Brauer second main theorem relates the values of irreducible characters of $G$ on the $p$-section associated to $x$ to values of characters in certain blocks of $C _ { G } ( x )$. |
| | | | |
| − | Suppose that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046016.png" /> is an irreducible character of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046017.png" /> (cf. also [[Character of a group|Character of a group]]), afforded by the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046018.png" />-free right <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046019.png" />-module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046020.png" />, and belonging to the [[Block|block]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046021.png" /> (cf. also [[Defect group of a block|Defect group of a block]]). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046022.png" /> be a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046023.png" />-element of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046024.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046025.png" />. For all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046026.png" />-subgroups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046027.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046028.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046029.png" />; hence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046030.png" /> is defined for all blocks <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046031.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046032.png" />. One can organize the block decomposition of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046033.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046034.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046035.png" /> be the projection of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046036.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046037.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046038.png" /> be the projection of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046039.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046040.png" />. The restriction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046041.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046042.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046043.png" /> can be decomposed as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046044.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046045.png" /> is the character of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046046.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046047.png" /> is the character of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046048.png" />, then of course <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046049.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046050.png" />. Brauer's second main theorem states that for all elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046051.png" /> of order prime to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046052.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046053.png" />. Thus, the values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046054.png" /> on the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046055.png" />-section associated to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046056.png" /> are determined in the blocks of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046057.png" /> sent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046058.png" /> by the Brauer correspondence (cf. also [[Brauer first main theorem|Brauer first main theorem]]). | + | Suppose that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046016.png"/> is an irreducible character of $G$ (cf. also [[Character of a group|Character of a group]]), afforded by the $R$-free right $R G$-module $V$, and belonging to the [[Block|block]] $B$ (cf. also [[Defect group of a block|Defect group of a block]]). Let $x$ be a $p$-element of $G$, and let $H = C _ { G } ( x )$. For all $p$-subgroups $D$ of $H$, $C _ { G } ( D ) \subseteq H$; hence $b ^ { G }$ is defined for all blocks $b$ of $R H$. One can organize the block decomposition of $R H$ as $R H = ( \oplus _ { b ^{ G} = B } b ) \oplus (\oplus_{ b ^{ G} \neq B } b )$. Let $e$ be the projection of $1$ on $( \oplus _ { b ^G = B } b )$, and let $f$ be the projection of $1$ on $( \oplus _ { b ^{ G } \neq B } b )$. The restriction $V _ { H }$ of $V$ to $H$ can be decomposed as $V _ { H } = V _ { H } e \oplus V _ { H } f$. If $\chi _ { e }$ is the character of $V _ { H }e$ and $\chi _ { f }$ is the character of $V _ { H } f$, then of course $\chi ( h ) = \chi _ { e } ( h ) + \chi_{f }( h )$ for all $h \in H$. Brauer's second main theorem states that for all elements $y \in H$ of order prime to $p$, $\chi _ { f } ( x y ) = 0$. Thus, the values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120460/b12046054.png"/> on the $p$-section associated to $x$ are determined in the blocks of $C _ { G } ( x )$ sent to $B$ by the Brauer correspondence (cf. also [[Brauer first main theorem|Brauer first main theorem]]). |
| | | | |
| | This theorem was first proved in [[#References|[a1]]]. See also [[#References|[a2]]], [[#References|[a3]]], and [[#References|[a4]]]. | | This theorem was first proved in [[#References|[a1]]]. See also [[#References|[a2]]], [[#References|[a3]]], and [[#References|[a4]]]. |
| | | | |
| | ====References==== | | ====References==== |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Brauer, "Zur Darstellungstheorie der Gruppen endlicher Ordnung II" ''Math. Z.'' , '''72''' (1959) pp. 22–46</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> C. Curtis, I. Reiner, "Methods of representation theory" , '''II''' , Wiley (1987)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Feit, "The representation theory of finite groups" , North-Holland (1982)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Nagao, Y. Tsushima, "Representation of finite groups" , Acad. Press (1987)</TD></TR></table> | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> R. Brauer, "Zur Darstellungstheorie der Gruppen endlicher Ordnung II" ''Math. Z.'' , '''72''' (1959) pp. 22–46</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> C. Curtis, I. Reiner, "Methods of representation theory" , '''II''' , Wiley (1987)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> W. Feit, "The representation theory of finite groups" , North-Holland (1982)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> H. Nagao, Y. Tsushima, "Representation of finite groups" , Acad. Press (1987)</td></tr></table> |
For notation and definitions, see Brauer first main theorem.
Let $x$ be an element of $G$ whose order is a power of $p$. The $p$-section of $G$ associated to $x$ is the set of all elements of $G$ whose $p$-part is conjugate to $x$. Brauer second main theorem relates the values of irreducible characters of $G$ on the $p$-section associated to $x$ to values of characters in certain blocks of $C _ { G } ( x )$.
Suppose that 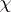 is an irreducible character of $G$ (cf. also Character of a group), afforded by the $R$-free right $R G$-module $V$, and belonging to the block $B$ (cf. also Defect group of a block). Let $x$ be a $p$-element of $G$, and let $H = C _ { G } ( x )$. For all $p$-subgroups $D$ of $H$, $C _ { G } ( D ) \subseteq H$; hence $b ^ { G }$ is defined for all blocks $b$ of $R H$. One can organize the block decomposition of $R H$ as $R H = ( \oplus _ { b ^{ G} = B } b ) \oplus (\oplus_{ b ^{ G} \neq B } b )$. Let $e$ be the projection of $1$ on $( \oplus _ { b ^G = B } b )$, and let $f$ be the projection of $1$ on $( \oplus _ { b ^{ G } \neq B } b )$. The restriction $V _ { H }$ of $V$ to $H$ can be decomposed as $V _ { H } = V _ { H } e \oplus V _ { H } f$. If $\chi _ { e }$ is the character of $V _ { H }e$ and $\chi _ { f }$ is the character of $V _ { H } f$, then of course $\chi ( h ) = \chi _ { e } ( h ) + \chi_{f }( h )$ for all $h \in H$. Brauer's second main theorem states that for all elements $y \in H$ of order prime to $p$, $\chi _ { f } ( x y ) = 0$. Thus, the values of
is an irreducible character of $G$ (cf. also Character of a group), afforded by the $R$-free right $R G$-module $V$, and belonging to the block $B$ (cf. also Defect group of a block). Let $x$ be a $p$-element of $G$, and let $H = C _ { G } ( x )$. For all $p$-subgroups $D$ of $H$, $C _ { G } ( D ) \subseteq H$; hence $b ^ { G }$ is defined for all blocks $b$ of $R H$. One can organize the block decomposition of $R H$ as $R H = ( \oplus _ { b ^{ G} = B } b ) \oplus (\oplus_{ b ^{ G} \neq B } b )$. Let $e$ be the projection of $1$ on $( \oplus _ { b ^G = B } b )$, and let $f$ be the projection of $1$ on $( \oplus _ { b ^{ G } \neq B } b )$. The restriction $V _ { H }$ of $V$ to $H$ can be decomposed as $V _ { H } = V _ { H } e \oplus V _ { H } f$. If $\chi _ { e }$ is the character of $V _ { H }e$ and $\chi _ { f }$ is the character of $V _ { H } f$, then of course $\chi ( h ) = \chi _ { e } ( h ) + \chi_{f }( h )$ for all $h \in H$. Brauer's second main theorem states that for all elements $y \in H$ of order prime to $p$, $\chi _ { f } ( x y ) = 0$. Thus, the values of 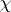 on the $p$-section associated to $x$ are determined in the blocks of $C _ { G } ( x )$ sent to $B$ by the Brauer correspondence (cf. also Brauer first main theorem).
on the $p$-section associated to $x$ are determined in the blocks of $C _ { G } ( x )$ sent to $B$ by the Brauer correspondence (cf. also Brauer first main theorem).
This theorem was first proved in [a1]. See also [a2], [a3], and [a4].
References
| [a1] | R. Brauer, "Zur Darstellungstheorie der Gruppen endlicher Ordnung II" Math. Z. , 72 (1959) pp. 22–46 |
| [a2] | C. Curtis, I. Reiner, "Methods of representation theory" , II , Wiley (1987) |
| [a3] | W. Feit, "The representation theory of finite groups" , North-Holland (1982) |
| [a4] | H. Nagao, Y. Tsushima, "Representation of finite groups" , Acad. Press (1987) |
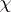 is an irreducible character of $G$ (cf. also Character of a group), afforded by the $R$-free right $R G$-module $V$, and belonging to the block $B$ (cf. also Defect group of a block). Let $x$ be a $p$-element of $G$, and let $H = C _ { G } ( x )$. For all $p$-subgroups $D$ of $H$, $C _ { G } ( D ) \subseteq H$; hence $b ^ { G }$ is defined for all blocks $b$ of $R H$. One can organize the block decomposition of $R H$ as $R H = ( \oplus _ { b ^{ G} = B } b ) \oplus (\oplus_{ b ^{ G} \neq B } b )$. Let $e$ be the projection of $1$ on $( \oplus _ { b ^G = B } b )$, and let $f$ be the projection of $1$ on $( \oplus _ { b ^{ G } \neq B } b )$. The restriction $V _ { H }$ of $V$ to $H$ can be decomposed as $V _ { H } = V _ { H } e \oplus V _ { H } f$. If $\chi _ { e }$ is the character of $V _ { H }e$ and $\chi _ { f }$ is the character of $V _ { H } f$, then of course $\chi ( h ) = \chi _ { e } ( h ) + \chi_{f }( h )$ for all $h \in H$. Brauer's second main theorem states that for all elements $y \in H$ of order prime to $p$, $\chi _ { f } ( x y ) = 0$. Thus, the values of
is an irreducible character of $G$ (cf. also Character of a group), afforded by the $R$-free right $R G$-module $V$, and belonging to the block $B$ (cf. also Defect group of a block). Let $x$ be a $p$-element of $G$, and let $H = C _ { G } ( x )$. For all $p$-subgroups $D$ of $H$, $C _ { G } ( D ) \subseteq H$; hence $b ^ { G }$ is defined for all blocks $b$ of $R H$. One can organize the block decomposition of $R H$ as $R H = ( \oplus _ { b ^{ G} = B } b ) \oplus (\oplus_{ b ^{ G} \neq B } b )$. Let $e$ be the projection of $1$ on $( \oplus _ { b ^G = B } b )$, and let $f$ be the projection of $1$ on $( \oplus _ { b ^{ G } \neq B } b )$. The restriction $V _ { H }$ of $V$ to $H$ can be decomposed as $V _ { H } = V _ { H } e \oplus V _ { H } f$. If $\chi _ { e }$ is the character of $V _ { H }e$ and $\chi _ { f }$ is the character of $V _ { H } f$, then of course $\chi ( h ) = \chi _ { e } ( h ) + \chi_{f }( h )$ for all $h \in H$. Brauer's second main theorem states that for all elements $y \in H$ of order prime to $p$, $\chi _ { f } ( x y ) = 0$. Thus, the values of 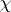 on the $p$-section associated to $x$ are determined in the blocks of $C _ { G } ( x )$ sent to $B$ by the Brauer correspondence (cf. also Brauer first main theorem).
on the $p$-section associated to $x$ are determined in the blocks of $C _ { G } ( x )$ sent to $B$ by the Brauer correspondence (cf. also Brauer first main theorem).