Brauer height-zero conjecture
For notation and definitions, see also Brauer first main theorem.
Let  be an irreducible character in a block
be an irreducible character in a block  of a group
of a group  with defect group
with defect group  (cf. also Defect group of a block). Let
(cf. also Defect group of a block). Let  be the discrete valuation defined on the integers with
be the discrete valuation defined on the integers with  whenever
whenever  is prime to
is prime to  . By a theorem of Brauer,
. By a theorem of Brauer,  . The height of
. The height of 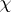 is defined to be
is defined to be
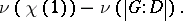 |
Every block contains an irreducible character of height zero. Brauer's height-zero conjecture is the assertion that every irreducible character in 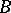 has height zero if and only if
has height zero if and only if 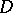 is Abelian (cf. also Abelian group).
is Abelian (cf. also Abelian group).
That every irreducible character in 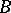 has height zero when
has height zero when 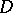 is Abelian was proved for
is Abelian was proved for 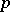 -solvable groups (cf. also
-solvable groups (cf. also 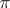 -solvable group) by P. Fong (see [a2], X.4). The converse for
-solvable group) by P. Fong (see [a2], X.4). The converse for 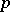 -solvable groups was proved by D. Gluck and T. Wolf [a3], using the classification of finite simple groups. The "if" direction has been reduced to the consideration of quasi-simple groups by T.R. Berger and R. Knörr [a1]. The task of checking this half of the conjecture for the quasisimple groups was completed in 2011 by R. Kessar and G. Malle [a4], hence completing the proof of the "if" direction. The evidence for the "only if" direction is more slender.
-solvable groups was proved by D. Gluck and T. Wolf [a3], using the classification of finite simple groups. The "if" direction has been reduced to the consideration of quasi-simple groups by T.R. Berger and R. Knörr [a1]. The task of checking this half of the conjecture for the quasisimple groups was completed in 2011 by R. Kessar and G. Malle [a4], hence completing the proof of the "if" direction. The evidence for the "only if" direction is more slender.
References
| [a1] | T.R. Berger, R. Knörr, "On Brauer's height  conjecture" Nagoya Math. J. , 109 (1988) pp. 109–116 conjecture" Nagoya Math. J. , 109 (1988) pp. 109–116 |
| [a2] | W. Feit, "The representation theory of finite groups" , North-Holland (1982) |
| [a3] | D. Gluck, T.R. Wolf, "Brauer's height conjecture for 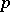 -solvable groups" Trans. Amer. Math. Soc. , 282 : 1 (1984) pp. 137–152 -solvable groups" Trans. Amer. Math. Soc. , 282 : 1 (1984) pp. 137–152 |
| [a4] | R. Kessar, G. Malle, "Quasi-isolated blocks and Brauer's height conjecture" arXiv:1112.2642 |
Brauer height-zero conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brauer_height-zero_conjecture&oldid=24289