Difference between revisions of "Boundary (in the theory of uniform algebras)"
(Importing text file) |
m (link) |
||
| Line 1: | Line 1: | ||
| − | A subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172901.png" /> of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172902.png" /> of maximal ideals of a [[Commutative Banach algebra|commutative Banach algebra]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172903.png" /> with an identity over the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172904.png" /> of complex numbers, on which the moduli of the Gel'fand transforms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172905.png" /> of all elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172906.png" /> attain their maximum (cf. [[Gel'fand representation|Gel'fand representation]]). For example, one can set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172907.png" /> (the trivial boundary). Of interest are non-trivial boundaries with some sort of minimality property. There exists among the closed boundaries <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172908.png" /> a minimal one <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172909.png" />, that is, a closed boundary such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729010.png" /> for every closed boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729011.png" />; it is called the Shilov boundary. The points of the Shilov boundary are characterized by the property that for each neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729012.png" /> of such a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729013.png" /> and every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729014.png" />, there exists an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729015.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729016.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729017.png" /> outside <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729018.png" />. The points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729019.png" /> constitute "the most stable" part of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729020.png" /> of maximal ideals: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729021.png" /> is a commutative Banach algebra containing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729022.png" /> as a subalgebra, then the maximal ideals (multiplicative functionals) corresponding to such points can be extended to maximal ideals (multiplicative functionals) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729023.png" />, whereas for maximal ideals not belonging to the boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729024.png" /> such an extension is, in general, not possible. This situation is analogous to the stability of the boundary of the spectrum of a bounded linear operator on a Banach space. A typical example is the algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729025.png" /> consisting of the functions continuous on the disc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729026.png" /> that are analytic for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729027.png" />. In this case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729028.png" /> can be identified with the closed disc and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729029.png" /> with its topological boundary; maximal ideals corresponding to interior points of the disc cannot be extended to maximal ideals of the algebra of all functions continuous on the boundary in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729030.png" /> is naturally included (according to the maximum principle), while the maximal ideals corresponding to the boundary points can be extended. | + | A subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172901.png" /> of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172902.png" /> of maximal ideals of a [[Commutative Banach algebra|commutative Banach algebra]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172903.png" /> with an identity over the field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172904.png" /> of complex numbers, on which the moduli of the Gel'fand transforms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172905.png" /> of all elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172906.png" /> attain their maximum (cf. [[Gel'fand representation|Gel'fand representation]]). For example, one can set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172907.png" /> (the trivial boundary). Of interest are non-trivial boundaries with some sort of minimality property. There exists among the closed boundaries <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172908.png" /> a minimal one <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b0172909.png" />, that is, a closed boundary such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729010.png" /> for every closed boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729011.png" />; it is called the ''[[Shilov boundary]]''. The points of the Shilov boundary are characterized by the property that for each neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729012.png" /> of such a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729013.png" /> and every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729014.png" />, there exists an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729015.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729016.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729017.png" /> outside <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729018.png" />. The points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729019.png" /> constitute "the most stable" part of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729020.png" /> of maximal ideals: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729021.png" /> is a commutative Banach algebra containing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729022.png" /> as a subalgebra, then the maximal ideals (multiplicative functionals) corresponding to such points can be extended to maximal ideals (multiplicative functionals) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729023.png" />, whereas for maximal ideals not belonging to the boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729024.png" /> such an extension is, in general, not possible. This situation is analogous to the stability of the boundary of the spectrum of a bounded linear operator on a Banach space. A typical example is the algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729025.png" /> consisting of the functions continuous on the disc <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729026.png" /> that are analytic for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729027.png" />. In this case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729028.png" /> can be identified with the closed disc and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729029.png" /> with its topological boundary; maximal ideals corresponding to interior points of the disc cannot be extended to maximal ideals of the algebra of all functions continuous on the boundary in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729030.png" /> is naturally included (according to the maximum principle), while the maximal ideals corresponding to the boundary points can be extended. |
As in the case of algebras of analytic functions there is a local maximum-modulus principle for general commutative Banach algebras: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729031.png" /> is an open subset of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729032.png" />, then | As in the case of algebras of analytic functions there is a local maximum-modulus principle for general commutative Banach algebras: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729031.png" /> is an open subset of the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017290/b01729032.png" />, then | ||
Revision as of 13:42, 6 March 2018
A subset 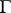 of the space
of the space 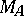 of maximal ideals of a commutative Banach algebra
of maximal ideals of a commutative Banach algebra 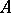 with an identity over the field
with an identity over the field 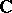 of complex numbers, on which the moduli of the Gel'fand transforms
of complex numbers, on which the moduli of the Gel'fand transforms 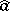 of all elements
of all elements 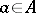 attain their maximum (cf. Gel'fand representation). For example, one can set
attain their maximum (cf. Gel'fand representation). For example, one can set 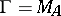 (the trivial boundary). Of interest are non-trivial boundaries with some sort of minimality property. There exists among the closed boundaries
(the trivial boundary). Of interest are non-trivial boundaries with some sort of minimality property. There exists among the closed boundaries 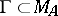 a minimal one
a minimal one 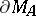 , that is, a closed boundary such that
, that is, a closed boundary such that 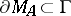 for every closed boundary
for every closed boundary 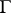 ; it is called the Shilov boundary. The points of the Shilov boundary are characterized by the property that for each neighbourhood
; it is called the Shilov boundary. The points of the Shilov boundary are characterized by the property that for each neighbourhood 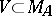 of such a point
of such a point 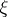 and every
and every 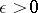 , there exists an element
, there exists an element 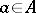 for which
for which 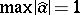 and
and  outside
outside 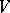 . The points
. The points 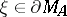 constitute "the most stable" part of the set
constitute "the most stable" part of the set  of maximal ideals: If
of maximal ideals: If 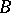 is a commutative Banach algebra containing
is a commutative Banach algebra containing  as a subalgebra, then the maximal ideals (multiplicative functionals) corresponding to such points can be extended to maximal ideals (multiplicative functionals) of
as a subalgebra, then the maximal ideals (multiplicative functionals) corresponding to such points can be extended to maximal ideals (multiplicative functionals) of  , whereas for maximal ideals not belonging to the boundary
, whereas for maximal ideals not belonging to the boundary 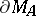 such an extension is, in general, not possible. This situation is analogous to the stability of the boundary of the spectrum of a bounded linear operator on a Banach space. A typical example is the algebra
such an extension is, in general, not possible. This situation is analogous to the stability of the boundary of the spectrum of a bounded linear operator on a Banach space. A typical example is the algebra  consisting of the functions continuous on the disc
consisting of the functions continuous on the disc 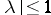 that are analytic for
that are analytic for 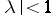 . In this case
. In this case 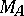 can be identified with the closed disc and
can be identified with the closed disc and 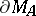 with its topological boundary; maximal ideals corresponding to interior points of the disc cannot be extended to maximal ideals of the algebra of all functions continuous on the boundary in which
with its topological boundary; maximal ideals corresponding to interior points of the disc cannot be extended to maximal ideals of the algebra of all functions continuous on the boundary in which 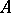 is naturally included (according to the maximum principle), while the maximal ideals corresponding to the boundary points can be extended.
is naturally included (according to the maximum principle), while the maximal ideals corresponding to the boundary points can be extended.
As in the case of algebras of analytic functions there is a local maximum-modulus principle for general commutative Banach algebras: If 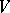 is an open subset of the space
is an open subset of the space 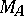 , then
, then
 |
for all  , where
, where 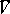 is the closure and
is the closure and  is the topological boundary of
is the topological boundary of 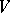 in
in 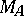 . Roughly speaking, this means that a local maximum point is necessarily a global maximum point (possibly of another element).
. Roughly speaking, this means that a local maximum point is necessarily a global maximum point (possibly of another element).
The notion of a boundary is used in the study of uniform algebras, that is, closed subalgebras 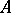 of the algebra
of the algebra 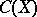 of all continuous functions on a compactum
of all continuous functions on a compactum 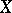 that separate points and contain the constants. In this situation
that separate points and contain the constants. In this situation 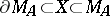 . There exists for each point
. There exists for each point 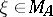 a representing measure, concentrated on the Shilov boundary, that is, a probability measure
a representing measure, concentrated on the Shilov boundary, that is, a probability measure 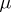 such that
such that
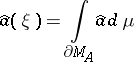 |
for all 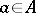 (this holds for arbitrary commutative Banach algebras). In the simplest case (described above) of the disc and the algebra of analytic functions, the latter formula reduces to the Poisson formula. The representing measure
(this holds for arbitrary commutative Banach algebras). In the simplest case (described above) of the disc and the algebra of analytic functions, the latter formula reduces to the Poisson formula. The representing measure 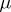 is in general not unique. For points belonging to the same Gleason part (see Algebra of functions), the measures
is in general not unique. For points belonging to the same Gleason part (see Algebra of functions), the measures 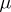 can be chosen absolutely continuous with respect to one another, which, under certain extra conditions of uniqueness type for the representing measures, makes it possible to equip the Gleason parts of the space of maximal ideals with a one-dimensional analytic structure compatible with the algebra. Every point of the Shilov boundary of a uniform algebra constitutes a one-point Gleason part; however, the converse is in general false.
can be chosen absolutely continuous with respect to one another, which, under certain extra conditions of uniqueness type for the representing measures, makes it possible to equip the Gleason parts of the space of maximal ideals with a one-dimensional analytic structure compatible with the algebra. Every point of the Shilov boundary of a uniform algebra constitutes a one-point Gleason part; however, the converse is in general false.
The equality 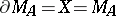 for uniform algebras is a simple necessary condition for the coincidence of
for uniform algebras is a simple necessary condition for the coincidence of 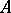 with
with 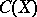 . Without extra hypotheses this is not a sufficient condition for the above coincidence even in the case of algebras
. Without extra hypotheses this is not a sufficient condition for the above coincidence even in the case of algebras 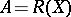 of uniform limits of rational functions on a compactum
of uniform limits of rational functions on a compactum 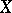 in the plane.
in the plane.
Let 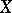 be a metrizable compactum and let
be a metrizable compactum and let 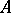 be a uniform algebra on
be a uniform algebra on 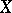 . Then there exists a minimal boundary among all the boundaries:
. Then there exists a minimal boundary among all the boundaries: 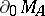 . The closure of the minimal boundary is the same as
. The closure of the minimal boundary is the same as 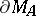 . However,
. However, 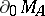 is, in general, not closed; an example is the subalgebra of all analytic functions inside the disc
is, in general, not closed; an example is the subalgebra of all analytic functions inside the disc  for which
for which 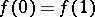 . The boundary
. The boundary 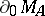 is the same as the set of peak points with respect to
is the same as the set of peak points with respect to 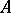 , that is, points
, that is, points 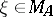 for which there exists an
for which there exists an 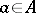 with
with 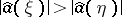 for all
for all 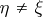 . On the other hand, a condition for a point
. On the other hand, a condition for a point 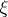 to belong to
to belong to 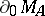 that is formally considerably weaker is known. Namely, if the point
that is formally considerably weaker is known. Namely, if the point 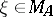 is such that for some
is such that for some 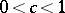 and
and 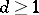 there exists for each neighbourhood
there exists for each neighbourhood 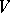 of
of 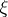 an element
an element  in
in 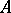 for which
for which 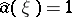 ,
, 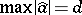 and
and 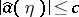 for
for 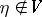 , then
, then 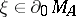 . The abstract Poisson formula has been strengthened in the following way: There exists for any point
. The abstract Poisson formula has been strengthened in the following way: There exists for any point 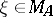 a representing measure concentrated on
a representing measure concentrated on 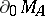 (
(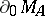 being, moreover, a
being, moreover, a 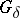 -set). In this form it has been successfully applied in certain problems of approximation theory. The points
-set). In this form it has been successfully applied in certain problems of approximation theory. The points 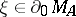 are characterized by the property that for these points, the measure is unique and is the same as the Dirac
are characterized by the property that for these points, the measure is unique and is the same as the Dirac 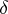 -measure, that is, the minimal boundary is a special case of the Choquet boundary.
-measure, that is, the minimal boundary is a special case of the Choquet boundary.
For the algebra 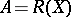 of uniform limits of rational functions on a compactum
of uniform limits of rational functions on a compactum 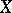 in the plane,
in the plane,  and
and 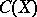 coincide if and only if
coincide if and only if 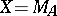 and
and 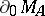 coincide. This is not true for arbitrary uniform algebras: There exists a uniform algebra
coincide. This is not true for arbitrary uniform algebras: There exists a uniform algebra  distinct from
distinct from 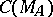 for which
for which 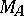 is metrizable and for which each point
is metrizable and for which each point 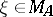 is a peak point (that is,
is a peak point (that is, 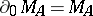 ). There also exists a uniform algebra for which all the Gleason parts are trivial (singletons), but for which even the Shilov boundary is a proper part of the space of maximal ideals.
). There also exists a uniform algebra for which all the Gleason parts are trivial (singletons), but for which even the Shilov boundary is a proper part of the space of maximal ideals.
One of the algebraic generalizations of the notion of the Shilov boundary is the following. Let 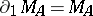 and let
and let  be the closed ideal generated by a set of elements
be the closed ideal generated by a set of elements 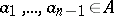 ,
, 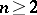 . The space
. The space 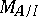 can be naturally identified with the set of common zeros of the functions
can be naturally identified with the set of common zeros of the functions  . The closure of the union of the boundaries
. The closure of the union of the boundaries 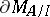 over all ideals
over all ideals  generated by
generated by 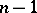 elements is denoted by
elements is denoted by 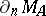 . For example, for the algebra of continuous functions in the polydisc
. For example, for the algebra of continuous functions in the polydisc 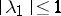 ,
, 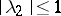 that are analytic in its interior,
that are analytic in its interior, 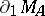 is the skeleton
is the skeleton 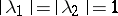 ,
, 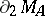 is the topological boundary
is the topological boundary 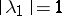 ,
, 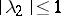 ;
; 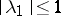 ,
, 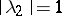 , and
, and 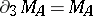 . These generalizations are useful when proving theorems on multi-dimensional analytic structures in spaces of maximal ideals.
. These generalizations are useful when proving theorems on multi-dimensional analytic structures in spaces of maximal ideals.
Notions of boundaries (or functional boundaries) similar to the ones described above are encountered in the theory of analytic functions (the Bergman boundary), probability theory (the Martin boundary) and in a number of other branches of mathematics. In this connection the initial set is not necessarily assumed to be an algebra or a ring.
References
| [1] | R. Basener, "A generalized Shilov boundary and analytic structure" Proc. Amer. Math. Soc. , 47 : 1 (1975) pp. 98–104 |
| [2] | A. Browder, "Introduction to function algebras" , Benjamin (1969) |
| [3] | T.W. Gamelin, "Uniform algebras" , Prentice-Hall (1969) |
| [4] | I.M. [I.M. Gel'fand] Gelfand, D.A. [D.A. Raikov] Raikov, G.E. [G.E. Shilov] Schilow, "Kommutative Normierte Ringe" , Deutsch. Verlag Wissenschaft. (1964) (Translated from Russian) |
| [5] | A.A. Gonchar, "The minimal boundary of the algebra 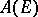 " Izv. Akad. Nauk SSSR Ser. Mat. , 27 : 4 (1963) pp. 949–955 (In Russian) " Izv. Akad. Nauk SSSR Ser. Mat. , 27 : 4 (1963) pp. 949–955 (In Russian) |
| [6] | R.R. Phelps, "Lectures on Choquet's theorem" , v. Nostrand (1966) |
Comments
Much of this article, in particular the definition of boundary, is relevant and valid for general commutative Banach algebras.
Boundary (in the theory of uniform algebras). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boundary_(in_the_theory_of_uniform_algebras)&oldid=16227