Borel-Lebesgue covering theorem
Let  be a bounded closed set in
be a bounded closed set in  and let
and let  be an open covering of it, i.e. a system of open sets the union of which contains
be an open covering of it, i.e. a system of open sets the union of which contains  ; then there exists a finite subsystem of sets
; then there exists a finite subsystem of sets  ,
,  , in
, in  (a subcovering) which is also a covering of
(a subcovering) which is also a covering of  , i.e.
, i.e.
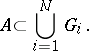 |
The Borel–Lebesgue theorem has a converse: If 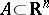 and if a finite subcovering may be extracted from any open covering of
and if a finite subcovering may be extracted from any open covering of  , then
, then  is closed and bounded. The possibility of extracting a finite subcovering out of any open covering of a set
is closed and bounded. The possibility of extracting a finite subcovering out of any open covering of a set 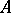 is often taken to be the definition of the set
is often taken to be the definition of the set  to be compact. According to such a terminology, the Borel–Lebesgue theorem and the converse theorem assume the following form: For a set
to be compact. According to such a terminology, the Borel–Lebesgue theorem and the converse theorem assume the following form: For a set  to be compact it is necessary and sufficient for
to be compact it is necessary and sufficient for  to be bounded and closed. The theorem was proved in 1898 by E. Borel [1] for the case when
to be bounded and closed. The theorem was proved in 1898 by E. Borel [1] for the case when  is a segment
is a segment  and
and 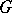 is a system of intervals; the theorem was given its ultimate form by H. Lebesgue [2] in 1900–1910. Alternative names for the theorem are Borel lemma, Heine–Borel lemma, Heine–Borel theorem.
is a system of intervals; the theorem was given its ultimate form by H. Lebesgue [2] in 1900–1910. Alternative names for the theorem are Borel lemma, Heine–Borel lemma, Heine–Borel theorem.
References
| [1] | E. Borel, "Leçons sur la théorie des fonctions" , Gauthier-Villars (1928) |
| [2] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) |
Borel-Lebesgue covering theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Borel-Lebesgue_covering_theorem&oldid=16019