Bitsadze-Lavrent'ev problem
Tricomi–Bitsadze–Lavrent'ev problem
The problem of finding a function 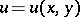 which satisfies
which satisfies
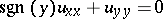 | (a1) |
in a mixed domain that is simply connected and bounded by a Jordan (non-self-intersecting) "elliptic" arc 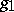 (for
(for 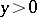 ) with end-points
) with end-points 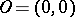 and
and  and by the "real" characteristics (for
and by the "real" characteristics (for 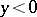 )
)
 |
of the Bitsadze–Lavrent'ev equation (a1), which satisfy the characteristic equation
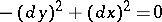 |
and meet at the point 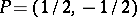 , and which assumes prescribed continuous boundary values
, and which assumes prescribed continuous boundary values
 | (a2) |
where  is the arc length reckoned from the point
is the arc length reckoned from the point  and
and
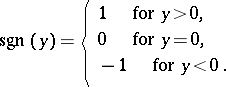 |
Consider the aforementioned domain (denoted by  ). Then a function
). Then a function  is a regular solution of the Bitsadze–Lavrent'ev problem if it satisfies the following conditions:
is a regular solution of the Bitsadze–Lavrent'ev problem if it satisfies the following conditions:
1)  is continuous in
is continuous in 
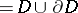 ,
, 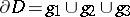 ;
;
2) 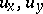 are continuous in
are continuous in 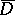 (except, possibly, at the points
(except, possibly, at the points 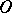 and
and 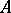 , where they may have poles of order less than
, where they may have poles of order less than 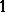 , i.e., they may tend to infinity with order less than
, i.e., they may tend to infinity with order less than 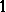 as
as 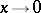 and
and 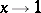 );
);
3)  ,
, 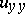 are continuous in
are continuous in 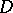 (except possibly on
(except possibly on 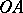 , where they need not exist);
, where they need not exist);
4)  satisfies (a1) at all points
satisfies (a1) at all points  (i.e.,
(i.e., 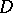 without
without 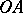 );
);
5)  satisfies the boundary conditions (a2).
satisfies the boundary conditions (a2).
Consider the normal curve (of Bitsadze–Lavrent'ev)
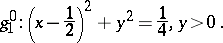 |
Note that it is the upper semi-circle and can also be given by (the upper part of)
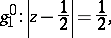 |
where 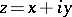 . The curve
. The curve 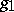 contains
contains 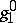 in its interior.
in its interior.
The idea of A.V. Bitsadze and M.A. Lavrent'ev for finding regular solutions of the above problem is as follows. First, solve the problem N (in 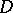 ,
, 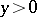 ). That is, find a regular solution of equation (a1) satisfying the boundary conditions:
). That is, find a regular solution of equation (a1) satisfying the boundary conditions:
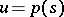 on
on 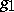 ;
;
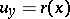 on
on 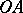 , where
, where 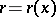 is continuous for
is continuous for  ,
, 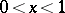 , and may tend to infinity of order less than
, and may tend to infinity of order less than 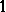 as
as 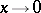 and
and 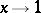 .
.
Secondly, solve the Cauchy–Goursat problem (in 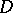 ,
, 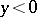 ). That is, find a regular solution of (a1) satisfying the boundary conditions:
). That is, find a regular solution of (a1) satisfying the boundary conditions:
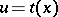 on
on 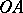 ;
;
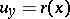 on
on 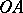 , where
, where 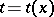 is continuous for
is continuous for  ,
, 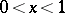 , and may tend to infinity of order less that
, and may tend to infinity of order less that 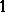 as
as 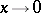 and
and  .
.
Finally, take into account the boundary condition
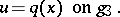 |
Therefore, one has a Goursat problem (in 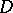 ,
, 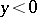 ) for (a1) with boundary conditions:
) for (a1) with boundary conditions:
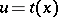 on
on 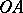 ;
;
 on
on 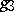 .
.
Several extensions and generalizations of the above boundary value problem of mixed type have been established [a3], [a4], [a5], [a6], [a7], [a8]. These problems are important in fluid mechanics (aerodynamics and hydrodynamics, [a1], [a2]).
References
| [a1] | A.V. Bitsadze, "Equations of mixed type" , Macmillan (1964) (In Russian) |
| [a2] | C. Ferrari, F.G. Tricomi, "Transonic aerodynamics" , Acad. Press (1968) (Translated from Italian) |
| [a3] | J.M. Rassias, "Mixed type equations" , 90 , Teubner (1986) |
| [a4] | J.M. Rassias, "Lecture notes on mixed type partial differential equations" , World Sci. (1990) |
| [a5] | J.M. Rassias, "The Bitsadze–Lavrentjev problem" Bull. Soc. Roy. Sci. Liège , 48 (1979) pp. 424–425 |
| [a6] | J.M. Rassias, "The bi-hyperbolic Bitsadze–Lavrentjev–Rassias problem in three-dimensional Euclidean space" C.R. Acad. Sci. Bulg. Sci. , 39 (1986) pp. 29–32 |
| [a7] | J.M. Rassias, "The mixed Bitsadze–Lavrentjev–Tricomi boundary value problem" , Texte zur Mathematik , 90 , Teubner (1986) pp. 6–21 |
| [a8] | J.M. Rassias, "The well posed Tricomi–Bitsadze–Lavrentjev problem in the Euclidean plane" Atti. Accad. Sci. Torino , 124 (1990) pp. 73–83 |
Bitsadze-Lavrent'ev problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bitsadze-Lavrent%27ev_problem&oldid=22131