Binomial series
A power series of the form
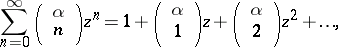 |
where  is an integer and
is an integer and 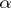 is an arbitrary fixed number (in general, a complex number),
is an arbitrary fixed number (in general, a complex number), 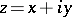 is a complex variable, and the
is a complex variable, and the
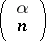 |
are the binomial coefficients. For an integer 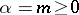 the binomial series reduces to a finite sum of
the binomial series reduces to a finite sum of 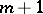 terms
terms
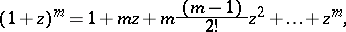 |
which is known as the Newton binomial. For other values of 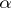 the binomial series converges absolutely for
the binomial series converges absolutely for 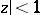 and diverges for
and diverges for 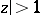 . At points of the unit circle
. At points of the unit circle  the binomial series behaves as follows: 1) if
the binomial series behaves as follows: 1) if 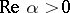 , it converges absolutely at all points; 2) if
, it converges absolutely at all points; 2) if 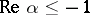 , it diverges at all points; and 3) if
, it diverges at all points; and 3) if 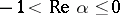 , the binomial series diverges at the point
, the binomial series diverges at the point 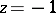 and converges conditionally at all other points. At all points of convergence, the binomial series represents the principal value of the function
and converges conditionally at all other points. At all points of convergence, the binomial series represents the principal value of the function 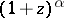 which is equal to one at
which is equal to one at 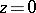 . The binomial series is a special case of a hypergeometric series.
. The binomial series is a special case of a hypergeometric series.
If  and
and 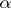 are real numbers, and
are real numbers, and 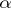 is not a non-negative integer, the binomial series behaves as follows: 1) if
is not a non-negative integer, the binomial series behaves as follows: 1) if 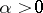 , it converges absolutely on
, it converges absolutely on 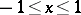 ; 2) if
; 2) if 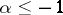 , it converges absolutely in
, it converges absolutely in 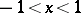 and diverges at all other values of
and diverges at all other values of  ; and 3) if
; and 3) if 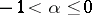 , the binomial series converges absolutely in
, the binomial series converges absolutely in 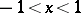 , converges conditionally at
, converges conditionally at 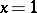 , and diverges for
, and diverges for 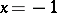 ; for
; for 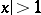 the binomial series always diverges.
the binomial series always diverges.
Binomial series were probably first mentioned by I. Newton in 1664–1665. An exhaustive study of binomial series was conducted by N.H. Abel [1], and was the starting point of the theory of complex power series.
References
| [1] | N.H. Abel, "Untersuchungen über die Reihe 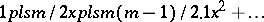 " J. Reine Angew. Math. , 1 (1826) pp. 311–339 " J. Reine Angew. Math. , 1 (1826) pp. 311–339 |
| [2] | K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) (English translation: Blackie, 1951 & Dover, reprint, 1990) |
| [3] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
Binomial series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Binomial_series&oldid=17445