Difference between revisions of "Binary tree"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
A (planar) rooted tree for which every node has a left child, a right child, neither, or both. Three examples are: | A (planar) rooted tree for which every node has a left child, a right child, neither, or both. Three examples are: | ||
| Line 7: | Line 8: | ||
These three are all different. | These three are all different. | ||
| − | The number of binary trees with | + | The number of binary trees with $n$ nodes, $p$ left children, $q$ right children ($p+q=n-1$) is |
| − | + | $$\frac1n\binom np\binom{n}{p+1}=\frac1n\binom np\binom nq.$$ | |
| − | The numbers | + | The numbers $n^{-1}\binom np\binom{n}{p+1}$ are called Runyon numbers or Narayama numbers. |
A complete binary tree is one in which every node has both left and right children or is a leaf (i.e., has no children). E.g., there are two complete binary trees with five nodes: | A complete binary tree is one in which every node has both left and right children or is a leaf (i.e., has no children). E.g., there are two complete binary trees with five nodes: | ||
| Line 19: | Line 20: | ||
Figure: b110530b | Figure: b110530b | ||
| − | A complete binary tree has an odd number of nodes, say | + | A complete binary tree has an odd number of nodes, say $2k+1$, and then the number of leaves is $k+1$. Label the $k+1$ leaves from left to right with symbols $x_1,\ldots,x_{k+1}$. Then the various complete binary trees with their $k+1$ leaves labelled in this order precisely correspond to all the different ways of putting brackets in the word $x_1\ldots x_{k+1}$, each way corresponding to a computation of the product by successive multiplications of precisely two factors each time. The number of ways of doing this, and hence the number of binary trees with $k+1$ nodes, is the Catalan number |
| − | + | $$\frac{1}{k+1}\binom{2k}{k},k=1,2,\ldots.$$ | |
The problem of all such bracketings of a product (of numbers) was considered by E. Catalan in 1838 [[#References|[a1]]]. | The problem of all such bracketings of a product (of numbers) was considered by E. Catalan in 1838 [[#References|[a1]]]. | ||
| − | The correspondence between complete binary trees and (complete) bracketings gives a bijection between complete binary trees with leaves labelled with elements from a set | + | The correspondence between complete binary trees and (complete) bracketings gives a bijection between complete binary trees with leaves labelled with elements from a set $X$ and the [[Free magma|free magma]] on $X$. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Catalan, "Note sur une équation aux différences finies" ''J. Math. Pures Appl.'' , '''3''' (1838) pp. 508–516</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L. Comtet, "Advanced combinatorics" , Reidel (1974)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> I.M. Gessel, R.P. Stanley, "Algebraic enumeration" R.L. Graham (ed.) M. Grötschel (ed.) L. Lovacz (ed.) , ''Handbook of Combinatorics'' , '''II''' , Elsevier (1995) pp. 1021–1062</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> R.P. Stanley, "Enumerative combinatorics" , Wadsworth and Brooks/Cole (1986)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Catalan, "Note sur une équation aux différences finies" ''J. Math. Pures Appl.'' , '''3''' (1838) pp. 508–516</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L. Comtet, "Advanced combinatorics" , Reidel (1974)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> I.M. Gessel, R.P. Stanley, "Algebraic enumeration" R.L. Graham (ed.) M. Grötschel (ed.) L. Lovacz (ed.) , ''Handbook of Combinatorics'' , '''II''' , Elsevier (1995) pp. 1021–1062</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> R.P. Stanley, "Enumerative combinatorics" , Wadsworth and Brooks/Cole (1986)</TD></TR></table> | ||
Revision as of 09:40, 12 April 2014
A (planar) rooted tree for which every node has a left child, a right child, neither, or both. Three examples are:

Figure: b110530a
These three are all different.
The number of binary trees with $n$ nodes, $p$ left children, $q$ right children ($p+q=n-1$) is
$$\frac1n\binom np\binom{n}{p+1}=\frac1n\binom np\binom nq.$$
The numbers $n^{-1}\binom np\binom{n}{p+1}$ are called Runyon numbers or Narayama numbers.
A complete binary tree is one in which every node has both left and right children or is a leaf (i.e., has no children). E.g., there are two complete binary trees with five nodes:
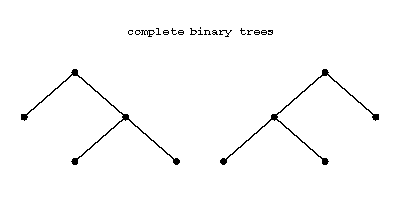
Figure: b110530b
A complete binary tree has an odd number of nodes, say $2k+1$, and then the number of leaves is $k+1$. Label the $k+1$ leaves from left to right with symbols $x_1,\ldots,x_{k+1}$. Then the various complete binary trees with their $k+1$ leaves labelled in this order precisely correspond to all the different ways of putting brackets in the word $x_1\ldots x_{k+1}$, each way corresponding to a computation of the product by successive multiplications of precisely two factors each time. The number of ways of doing this, and hence the number of binary trees with $k+1$ nodes, is the Catalan number
$$\frac{1}{k+1}\binom{2k}{k},k=1,2,\ldots.$$
The problem of all such bracketings of a product (of numbers) was considered by E. Catalan in 1838 [a1].
The correspondence between complete binary trees and (complete) bracketings gives a bijection between complete binary trees with leaves labelled with elements from a set $X$ and the free magma on $X$.
References
| [a1] | E. Catalan, "Note sur une équation aux différences finies" J. Math. Pures Appl. , 3 (1838) pp. 508–516 |
| [a2] | L. Comtet, "Advanced combinatorics" , Reidel (1974) |
| [a3] | I.M. Gessel, R.P. Stanley, "Algebraic enumeration" R.L. Graham (ed.) M. Grötschel (ed.) L. Lovacz (ed.) , Handbook of Combinatorics , II , Elsevier (1995) pp. 1021–1062 |
| [a4] | R.P. Stanley, "Enumerative combinatorics" , Wadsworth and Brooks/Cole (1986) |
Binary tree. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Binary_tree&oldid=31607