Bilinear form
on a product of modules 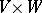
A bilinear mapping 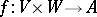 , where
, where 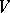 is a left unitary
is a left unitary 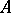 -module,
-module, 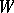 is a right unitary
is a right unitary 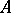 -module, and
-module, and 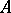 is a ring with a unit element, which is also regarded as an
is a ring with a unit element, which is also regarded as an 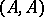 -bimodule. If
-bimodule. If 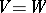 , one says that
, one says that 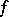 is a bilinear form on the module
is a bilinear form on the module 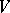 , and also that
, and also that 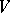 has a metric structure given by
has a metric structure given by 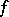 . Definitions involving bilinear mappings make sense also for bilinear forms. Thus, one speaks of the matrix of a bilinear form with respect to chosen bases in
. Definitions involving bilinear mappings make sense also for bilinear forms. Thus, one speaks of the matrix of a bilinear form with respect to chosen bases in 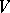 and
and 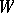 , of the orthogonality of elements and submodules with respect to bilinear forms, of orthogonal direct sums, of non-degeneracy, etc. For instance, if
, of the orthogonality of elements and submodules with respect to bilinear forms, of orthogonal direct sums, of non-degeneracy, etc. For instance, if 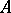 is a field and
is a field and 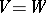 is a finite-dimensional vector space over
is a finite-dimensional vector space over 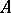 with basis
with basis  , then for the vectors
, then for the vectors
 |
and
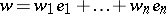 |
the value of the form will be
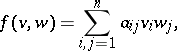 |
where 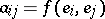 . The polynomial
. The polynomial  in the variables
in the variables 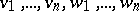 is sometimes identified with
is sometimes identified with 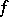 and is called a bilinear form on
and is called a bilinear form on 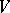 . If the ring
. If the ring 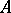 is commutative, a bilinear form is a special case of a sesquilinear form (with the identity automorphism).
is commutative, a bilinear form is a special case of a sesquilinear form (with the identity automorphism).
Let 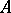 be a commutative ring. A bilinear form on an
be a commutative ring. A bilinear form on an 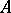 -module
-module 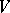 is said to be symmetric (or anti-symmetric or skew-symmetric) if for all
is said to be symmetric (or anti-symmetric or skew-symmetric) if for all 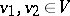 one has
one has 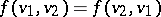 (or
(or 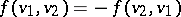 ), and is said to be alternating if
), and is said to be alternating if 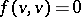 . An alternating bilinear form is anti-symmetric; the converse is true only if for any
. An alternating bilinear form is anti-symmetric; the converse is true only if for any 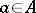 it follows from
it follows from 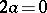 that
that 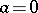 . If
. If 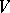 has a finite basis, symmetric (or anti-symmetric or alternating) forms on
has a finite basis, symmetric (or anti-symmetric or alternating) forms on 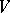 and only such forms have a symmetric (anti-symmetric, alternating) matrix in this basis. The orthogonality relation with respect to a symmetric or anti-symmetric form on
and only such forms have a symmetric (anti-symmetric, alternating) matrix in this basis. The orthogonality relation with respect to a symmetric or anti-symmetric form on 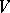 is symmetric.
is symmetric.
A bilinear form 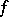 on
on 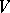 is said to be isometric with a bilinear form
is said to be isometric with a bilinear form 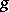 on
on 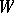 if there exists an isomorphism of
if there exists an isomorphism of 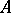 -modules
-modules 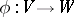 such that
such that
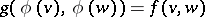 |
for all 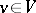 . This isomorphism is called an isometry of the form and, if
. This isomorphism is called an isometry of the form and, if 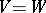 and
and 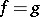 , a metric automorphism of the module
, a metric automorphism of the module 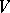 (or an automorphism of the form
(or an automorphism of the form 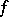 ). The metric automorphisms of a module form a group (the group of automorphisms of the form
). The metric automorphisms of a module form a group (the group of automorphisms of the form 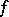 ); examples of such groups are the orthogonal group or the symplectic group.
); examples of such groups are the orthogonal group or the symplectic group.
Let 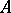 be a skew-field and let
be a skew-field and let 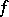 be a bilinear form on
be a bilinear form on 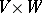 ; let the spaces
; let the spaces 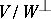 and
and 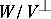 be finite-dimensional over
be finite-dimensional over 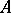 ; one then has
; one then has
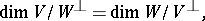 |
and this number is called the rank of 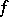 . If
. If 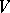 is finite-dimensional and
is finite-dimensional and 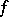 is non-degenerate, then
is non-degenerate, then
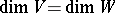 |
and for each basis  in
in 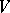 there exists a basis
there exists a basis  in
in 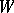 which is dual with respect to
which is dual with respect to 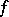 ; it is defined by the condition
; it is defined by the condition 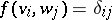 , where
, where 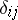 are the Kronecker symbols. If, in addition,
are the Kronecker symbols. If, in addition,  , then the submodules
, then the submodules 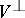 and
and 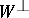 are said to be the right and the left kernel of
are said to be the right and the left kernel of 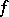 , respectively; for symmetric and anti-symmetric forms the right and left kernels are identical and are simply referred to as the kernel.
, respectively; for symmetric and anti-symmetric forms the right and left kernels are identical and are simply referred to as the kernel.
Let 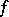 be a symmetric or an anti-symmetric bilinear form on
be a symmetric or an anti-symmetric bilinear form on 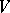 . An element
. An element 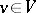 for which
for which 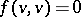 is said to be an isotropic element; a submodule
is said to be an isotropic element; a submodule 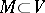 is said to be isotropic if
is said to be isotropic if 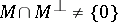 , and totally isotropic if
, and totally isotropic if 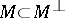 . Totally isotropic submodules play an important role in the study of the structure of bilinear forms (cf. Witt decomposition; Witt theorem; Witt ring). See also Quadratic form for the structure of bilinear forms.
. Totally isotropic submodules play an important role in the study of the structure of bilinear forms (cf. Witt decomposition; Witt theorem; Witt ring). See also Quadratic form for the structure of bilinear forms.
Let 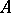 be commutative, let
be commutative, let 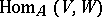 be the
be the 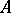 -module of all
-module of all 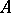 -linear mappings from
-linear mappings from  into
into  , and let
, and let 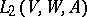 be the
be the 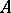 -module of all bilinear forms on
-module of all bilinear forms on 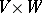 . For every bilinear form
. For every bilinear form 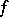 on
on 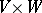 and for each
and for each 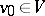 , the formula
, the formula
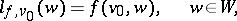 |
defines an 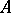 -linear form on
-linear form on 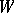 . Correspondingly, for
. Correspondingly, for 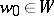 the formula
the formula
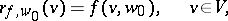 |
defines an 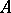 -linear form on
-linear form on 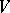 . The mapping
. The mapping 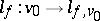 is an element of
is an element of
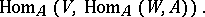 |
The mapping 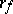 in
in
 |
is defined in a similar way. The mappings 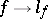 and
and  define isomorphisms between the
define isomorphisms between the  -modules
-modules
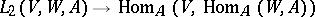 |
and
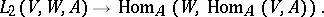 |
A bilinear form 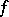 is said to be left-non-singular (respectively, right-non-singular) if
is said to be left-non-singular (respectively, right-non-singular) if 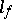 (respectively,
(respectively, 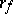 ) is an isomorphism; if
) is an isomorphism; if 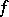 is both left- and right-non-singular, it is said to be non-singular; otherwise it is said to be singular. A non-degenerate bilinear form may be singular. For free modules
is both left- and right-non-singular, it is said to be non-singular; otherwise it is said to be singular. A non-degenerate bilinear form may be singular. For free modules 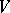 and
and 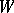 of the same finite dimension a bilinear form
of the same finite dimension a bilinear form 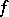 on
on 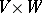 is non-singular if and only if the determinant of the matrix of
is non-singular if and only if the determinant of the matrix of 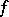 with respect to any bases in
with respect to any bases in 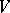 and
and 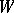 is an invertible element of the ring
is an invertible element of the ring 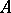 . The following isomorphisms
. The following isomorphisms
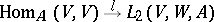 |
and
 |
given by a non-singular bilinear form 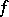 , are defined by the formulas
, are defined by the formulas
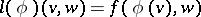 |
and
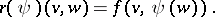 |
The endomorphisms 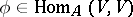 and
and 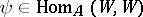 are said to be conjugate with respect to the form
are said to be conjugate with respect to the form 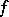 if
if 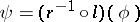 .
.
References
| [1] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) |
| [2] | S. Lang, "Algebra" , Addison-Wesley (1974) |
| [3] | E. Artin, "Geometric algebra" , Interscience (1957) |
Bilinear form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bilinear_form&oldid=17425