Difference between revisions of "Beurling algebra"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 121 formulas out of 123 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 123 formulas, 121 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
''of Fourier series with summable majorant of coefficients'' | ''of Fourier series with summable majorant of coefficients'' | ||
An algebra closely related to the Wiener algebra | An algebra closely related to the Wiener algebra | ||
| − | + | \begin{equation*} \mathcal{A} = \{ f : \| f \| _ { \mathcal{A} } = \sum _ { m = - \infty } ^ { \infty } | \hat { f } ( m ) | < \infty \}, \end{equation*} | |
where | where | ||
| − | + | \begin{equation*} \hat { f } ( m ) = ( 2 \pi ) ^ { - 1 } \int _ { - \pi } ^ { \pi } f ( u ) e ^ { - i m u } d u \end{equation*} | |
| − | is the | + | is the $m$th Fourier coefficient of $f$ (cf. also [[Fourier coefficients|Fourier coefficients]]). The Beurling algebra is defined as |
| − | + | \begin{equation*} \mathcal{A} ^ { * } = \left\{ f : \|\, f \| _ { \mathcal{A}^ { * } } = \sum _ { k = 0 } ^ { \infty } \operatorname { sup } _ { k \leq |m | < \infty } |\, \hat { f } ( m ) | < \infty \right\}. \end{equation*} | |
| − | The space | + | The space $\mathcal{A} ^ { * }$ was introduced by A. Beurling for establishing contraction properties of functions [[#References|[a2]]]: Let |
| − | + | \begin{equation*} f ( t ) = \sum _ { n = - \infty } ^ { \infty } a _ { n } e ^ { i n t } , a _ { 0 } = 0, \end{equation*} | |
| − | be an absolutely convergent [[Fourier series|Fourier series]] such that | + | be an absolutely convergent [[Fourier series|Fourier series]] such that $| a _ { \pm n } | \leq a _ { n } ^ { * }$, $n \geq 1$, where $\{ a _ { n } ^ { * } \}$ is a non-increasing sequence of numbers with a finite sum. Then if |
| − | + | \begin{equation*} g ( t ) \sim \sum _ { n = - \infty } ^ { \infty } b _ { n } e ^ { i n t } , b _ { 0 } = 0, \end{equation*} | |
| − | is a contraction of | + | is a contraction of $f ( t )$ (that is, for any pair of arguments $t_{1}$, $t_2$ the inequality $| g ( t _ { 1 } ) - g ( t _ { 2 } ) | \leq | f ( t _ { 1 } ) - f ( t _ { 2 } ) |$ holds), then the Fourier series of $g ( t )$ also converges absolutely, and |
| − | + | \begin{equation*} \sum _ { n = - \infty } ^ { \infty } | b _ { n } | \leq 10 \sum _ { n = 1 } ^ { \infty } a _ { n } ^ { * }. \end{equation*} | |
A similar result was proved in [[#References|[a2]]] for the [[Fourier transform|Fourier transform]], whence integrability of the monotone majorant on the real line is considered. These two spaces coincide locally, hence have much in common. | A similar result was proved in [[#References|[a2]]] for the [[Fourier transform|Fourier transform]], whence integrability of the monotone majorant on the real line is considered. These two spaces coincide locally, hence have much in common. | ||
| − | Subsequently, | + | Subsequently, $\mathcal{A} ^ { * }$ appeared in some other papers either in explicit or implicit form. See [[#References|[a1]]] for a detailed survey of the history and properties of $\mathcal{A} ^ { * }$. |
| − | It turned out that the consideration of summability of Fourier series by linear methods at Lebesgue points leads to the same space of functions. Let | + | It turned out that the consideration of summability of Fourier series by linear methods at Lebesgue points leads to the same space of functions. Let $f$ be a $2 \pi$-periodic integrable function with Fourier series $\sum _ { k } \hat { f } ( k ) e ^ { i k x }$. Let $\lambda$ be a continuous function on $\mathbf{R} = ( - \infty , \infty )$, representable as follows: |
| − | + | \begin{equation*} \lambda ( x ) = \int _ { \mathbf{R} } e ^ { - i x t } d \mu ( t ), \end{equation*} | |
| − | where | + | where $\mu$ is a finite [[Borel measure|Borel measure]] satisfying $\int _ { \mathbf{R} } d \mu ( t ) = 1$. Consider the means |
| − | + | \begin{equation*} ( f * d \mu ) _ { N } : = \operatorname { lim } _ { h \rightarrow 0 } \int _ { \mathbf{R} } f _ { h } \left( \frac { x - u } { N } \right) d \mu ( u ), \end{equation*} | |
where | where | ||
| − | + | \begin{equation*} f _ { h } ( x ) = h ^ { - 1 } \int _ {\bf R } \varphi \left( \frac { t } { h } \right) f ( x - t ) d t. \end{equation*} | |
| − | Here, | + | Here, $\varphi ( t )$ is infinitely differentiable, equal to $1$ for $|t | < 1$, vanishing for $| t | > 2$ and such that $\int _ { \mathbf R } \varphi ( t ) d t = 1$. For $f$ sufficiently smooth one has |
| − | + | \begin{equation*} ( f ^ { * } d \mu ) _ { N } ( x ) = \sum _ { k } \lambda \left( \frac { k } { N } \right) \hat { f } ( k ) e ^ { i k x }, \end{equation*} | |
| − | and these are the linear means of the [[Fourier series|Fourier series]] generated by | + | and these are the linear means of the [[Fourier series|Fourier series]] generated by $\lambda$. |
| − | The linear means | + | The linear means $( f ^ { * } d \mu ) _ { N } ( x )$ converge to $f ( x )$ as $N \rightarrow \infty$ at all the Lebesgue points of each integrable $f$ if and only if the measure $\mu$ is absolutely continuous (cf. [[Absolute continuity|Absolute continuity]]) with respect to the [[Lebesgue measure|Lebesgue measure]] and |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130120/b13012043.png"/></td> </tr></table> |
| − | + | $\mathcal{A} ^ { * }$ possesses many properties which are similar to those of $\mathcal{A}$: | |
| − | 1) | + | 1) $\mathcal{A} ^ { * }$ is a [[Banach algebra|Banach algebra]] with the local property. |
| − | 2) The space of maximal ideals (cf. also [[Maximal ideal|Maximal ideal]]) of | + | 2) The space of maximal ideals (cf. also [[Maximal ideal|Maximal ideal]]) of $\mathcal{A} ^ { * }$ coincides with $[- \pi , \pi ]$. |
| − | 3) | + | 3) $\mathcal{A} ^ { * }$ is a regular Banach algebra with trivial radical. |
| − | 4) If | + | 4) If $f \in \mathcal{A} ^ { * }$ and $F ( z )$ is defined and analytic on a neighbourhood of the set of values of the function $f$, then $F \circ f \in \mathcal{A} ^ { * }$ (in particular, if $f$ does not vanish anywhere, then $1 / f \in \mathcal{A} ^ { * }$). |
| − | The space | + | The space ${\cal P M} ^ { * }$ of all sequences $d = \{ d_{ k } \} ^ { \infty } _ { k = - \infty}$ with finite norm |
| − | + | \begin{equation*} \| d \| _ {\cal P M ^* } = \operatorname { sup } _ { n \geq 0 } \frac { 1 } { n + 1 } \sum _ { k = - n } ^ { n } | d _ { k } | \end{equation*} | |
| − | is the dual space of | + | is the dual space of $\mathcal{A} ^ { * }$. |
| − | The space | + | The space ${\cal P M} ^ { * }$ is not separable (cf. also [[Separable space|Separable space]]) and thus the space $\mathcal{A} ^ { * }$, like $\mathcal{A}$, is not reflexive (cf. also [[Reflexive space|Reflexive space]]). |
| − | ==Spectral properties of | + | ==Spectral properties of $\mathcal{A} ^ { * }$.== |
| − | The following two results are analogues for | + | The following two results are analogues for $\mathcal{A} ^ { * }$ of the Herz theorem and of the Wiener–Ditkin theorem, respectively. |
| − | Let | + | Let $f _ { N }$ be a function coinciding with $f$ at each point $2 \pi k / N$, where $k , N > 0$ are integers, $k < N$, and $f _ { N }$ is linear on intervals. Suppose $f \in \mathcal{A} ^ { * }$. Then |
| − | + | \begin{equation*} \operatorname { lim } _ { N \rightarrow \infty } \| f - f _ { N } \| _ { \cal A ^ { * } }= 0. \end{equation*} | |
| − | Let | + | Let $\Delta _ { \varepsilon } ( t ) = ( 1 - | t | / \varepsilon ) _ { + }$ for $t | \leq \pi$ and $\varepsilon \in ( 0 , \pi / 2 )$, $\Delta _ { \varepsilon } ( t + 2 \pi ) = \Delta _ { \varepsilon } ( t )$, and $V _ { \varepsilon } = 2 \Delta _ { 2 \varepsilon} - \Delta _ { \varepsilon }$. Let $f \in \mathcal{A} ^ { * }$ and $f ( 0 ) = 0$. Then |
| − | + | \begin{equation*} \operatorname { lim } _ { \varepsilon \rightarrow 0 } \| f V _ { \varepsilon } \| _ { \mathcal{A} } * = 0. \end{equation*} | |
==Synthesis problems.== | ==Synthesis problems.== | ||
| − | Writing | + | Writing $f \in S$ if $f$ admits synthesis in the norm of $\mathcal{A} ^ { * }$ (cf. also [[Synthesis problems|Synthesis problems]]), for $f \in \mathcal{A} ^ { * }$ the following statements hold. |
| − | a) If | + | a) If $f \in \operatorname { Lip } 1$, then $f \in S$ ($\operatorname { Lip } ( 1 / 2 )$ for $\mathcal{A}$). |
| − | b) If | + | b) If $f$ is absolutely continuous and in $\operatorname { Lip } \alpha$, $\alpha > 1 / 2$, then $f \in S$ (for $f \in \mathcal{A}$, $f$ has to be of bounded variation). |
| − | (Here, analogous conditions for | + | (Here, analogous conditions for $\mathcal{A}$ are given in parentheses; these assertions make up the Beurling–Pollard theorem.) |
| − | The following statements describe structural properties of functions in | + | The following statements describe structural properties of functions in $\mathcal{A} ^ { * }$. In the sequel, $\omega ( g , .)_p$ stands for the modulus of continuity, in the norm of $L ^ { p }$, of a function $g$ (cf. also [[Continuity, modulus of|Continuity, modulus of]]). |
| − | i) | + | i) $B _ { 1,1 } ^ { 1 } \subset \mathcal{A} ^ { * } \subset B _ { 2,1 } ^ { 1 / 2 }$, and the imbeddings into these Besov spaces (cf. also [[Nikol'skii space|Nikol'skii space]] and [[Hankel operator|Hankel operator]]) are both continuous. |
| − | ii) If | + | ii) If $f$ is absolutely continuous and |
| − | + | \begin{equation*} \int _ { 0 } ^ { 1 } \omega ( f ^ { \prime } ; t ) _ { p } \left( \operatorname { ln } \frac { 1 } { t } \right) ^ { - 1 / p ^ { \prime } } t ^ { - 1 } d t < \infty \end{equation*} | |
| − | for some | + | for some $p \in [ 1,2 ]$, $p ^ { \prime } = p / ( p - 1 )$, then $f \in \mathcal{A} ^ { * }$. |
| − | iii) There exists a continuously differentiable function | + | iii) There exists a continuously differentiable function $f \notin \mathcal{A} ^ { * }$ for which |
| − | + | \begin{equation*} \omega ( f ^ { \prime } ; t ) _ { \infty } = O \left( \left( \operatorname { ln } \frac { 1 } { t } \right) ^ { - 1 / 2 } \right). \end{equation*} | |
| − | The second inclusion in i) is sharp; indeed, for each | + | The second inclusion in i) is sharp; indeed, for each $\varepsilon > 0$ there exists a function $f \notin B _ { 2 , \infty } ^ { \varepsilon + 1 / 2 }$ such that $f \in \mathcal{A} ^ { * }$. As for ii), it is sharp for $p = 1$. The question is open for $p > 1$ (as of 2000). |
| − | There exists a function | + | There exists a function $f \in \mathcal{A} ^ { * }$ that is not of bounded variation (cf. also [[Function of bounded variation|Function of bounded variation]]). |
| − | The following condition, although being very simple, is surprisingly sharp. If | + | The following condition, although being very simple, is surprisingly sharp. If $f ^ { \prime } \in \mathcal{A}$, then $f \in \mathcal{A} ^ { * }$. If the Fourier series of $f$ is lacunary in the sense of Hadamard (cf. also [[Lacunary sequence|Lacunary sequence]]), then the converse statement holds. |
| − | Note that the central problem of [[Spectral synthesis|spectral synthesis]], that is, existence of sets that are not of synthesis as well as existence of functions not admitting synthesis, is still open (as of 2000) for | + | Note that the central problem of [[Spectral synthesis|spectral synthesis]], that is, existence of sets that are not of synthesis as well as existence of functions not admitting synthesis, is still open (as of 2000) for $\mathcal{A} ^ { * }$. |
| − | Another open question is connected with Beurling's initial result. It would be interesting to know whether the following statement, converse to that given above, is true or not: If for every | + | Another open question is connected with Beurling's initial result. It would be interesting to know whether the following statement, converse to that given above, is true or not: If for every $f \in \mathcal{A} ^ { * }$ one has $F \circ f \in \mathcal{A}$, then $F \in \operatorname { Lip } 1$. |
| − | Some of the results known for | + | Some of the results known for $\mathcal{A} ^ { * }$ have been generalized to the multi-dimensional case. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> E. Belinsky, E. Liflyand, R. Trigub, "The Banach algebra $A ^ { * }$ and its properties" ''J. Fourier Anal. Appl.'' , '''3''' (1997) pp. 103–129</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> A. Beurling, "On the spectral synthesis of bounded functions" ''Acta Math.'' , '''81''' (1949) pp. 225–238</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> J.-P. Kahane, "Séries de Fourier absolument convergentes" , Springer (1970)</td></tr></table> |
Revision as of 17:02, 1 July 2020
of Fourier series with summable majorant of coefficients
An algebra closely related to the Wiener algebra
\begin{equation*} \mathcal{A} = \{ f : \| f \| _ { \mathcal{A} } = \sum _ { m = - \infty } ^ { \infty } | \hat { f } ( m ) | < \infty \}, \end{equation*}
where
\begin{equation*} \hat { f } ( m ) = ( 2 \pi ) ^ { - 1 } \int _ { - \pi } ^ { \pi } f ( u ) e ^ { - i m u } d u \end{equation*}
is the $m$th Fourier coefficient of $f$ (cf. also Fourier coefficients). The Beurling algebra is defined as
\begin{equation*} \mathcal{A} ^ { * } = \left\{ f : \|\, f \| _ { \mathcal{A}^ { * } } = \sum _ { k = 0 } ^ { \infty } \operatorname { sup } _ { k \leq |m | < \infty } |\, \hat { f } ( m ) | < \infty \right\}. \end{equation*}
The space $\mathcal{A} ^ { * }$ was introduced by A. Beurling for establishing contraction properties of functions [a2]: Let
\begin{equation*} f ( t ) = \sum _ { n = - \infty } ^ { \infty } a _ { n } e ^ { i n t } , a _ { 0 } = 0, \end{equation*}
be an absolutely convergent Fourier series such that $| a _ { \pm n } | \leq a _ { n } ^ { * }$, $n \geq 1$, where $\{ a _ { n } ^ { * } \}$ is a non-increasing sequence of numbers with a finite sum. Then if
\begin{equation*} g ( t ) \sim \sum _ { n = - \infty } ^ { \infty } b _ { n } e ^ { i n t } , b _ { 0 } = 0, \end{equation*}
is a contraction of $f ( t )$ (that is, for any pair of arguments $t_{1}$, $t_2$ the inequality $| g ( t _ { 1 } ) - g ( t _ { 2 } ) | \leq | f ( t _ { 1 } ) - f ( t _ { 2 } ) |$ holds), then the Fourier series of $g ( t )$ also converges absolutely, and
\begin{equation*} \sum _ { n = - \infty } ^ { \infty } | b _ { n } | \leq 10 \sum _ { n = 1 } ^ { \infty } a _ { n } ^ { * }. \end{equation*}
A similar result was proved in [a2] for the Fourier transform, whence integrability of the monotone majorant on the real line is considered. These two spaces coincide locally, hence have much in common.
Subsequently, $\mathcal{A} ^ { * }$ appeared in some other papers either in explicit or implicit form. See [a1] for a detailed survey of the history and properties of $\mathcal{A} ^ { * }$.
It turned out that the consideration of summability of Fourier series by linear methods at Lebesgue points leads to the same space of functions. Let $f$ be a $2 \pi$-periodic integrable function with Fourier series $\sum _ { k } \hat { f } ( k ) e ^ { i k x }$. Let $\lambda$ be a continuous function on $\mathbf{R} = ( - \infty , \infty )$, representable as follows:
\begin{equation*} \lambda ( x ) = \int _ { \mathbf{R} } e ^ { - i x t } d \mu ( t ), \end{equation*}
where $\mu$ is a finite Borel measure satisfying $\int _ { \mathbf{R} } d \mu ( t ) = 1$. Consider the means
\begin{equation*} ( f * d \mu ) _ { N } : = \operatorname { lim } _ { h \rightarrow 0 } \int _ { \mathbf{R} } f _ { h } \left( \frac { x - u } { N } \right) d \mu ( u ), \end{equation*}
where
\begin{equation*} f _ { h } ( x ) = h ^ { - 1 } \int _ {\bf R } \varphi \left( \frac { t } { h } \right) f ( x - t ) d t. \end{equation*}
Here, $\varphi ( t )$ is infinitely differentiable, equal to $1$ for $|t | < 1$, vanishing for $| t | > 2$ and such that $\int _ { \mathbf R } \varphi ( t ) d t = 1$. For $f$ sufficiently smooth one has
\begin{equation*} ( f ^ { * } d \mu ) _ { N } ( x ) = \sum _ { k } \lambda \left( \frac { k } { N } \right) \hat { f } ( k ) e ^ { i k x }, \end{equation*}
and these are the linear means of the Fourier series generated by $\lambda$.
The linear means $( f ^ { * } d \mu ) _ { N } ( x )$ converge to $f ( x )$ as $N \rightarrow \infty$ at all the Lebesgue points of each integrable $f$ if and only if the measure $\mu$ is absolutely continuous (cf. Absolute continuity) with respect to the Lebesgue measure and
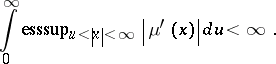 |
$\mathcal{A} ^ { * }$ possesses many properties which are similar to those of $\mathcal{A}$:
1) $\mathcal{A} ^ { * }$ is a Banach algebra with the local property.
2) The space of maximal ideals (cf. also Maximal ideal) of $\mathcal{A} ^ { * }$ coincides with $[- \pi , \pi ]$.
3) $\mathcal{A} ^ { * }$ is a regular Banach algebra with trivial radical.
4) If $f \in \mathcal{A} ^ { * }$ and $F ( z )$ is defined and analytic on a neighbourhood of the set of values of the function $f$, then $F \circ f \in \mathcal{A} ^ { * }$ (in particular, if $f$ does not vanish anywhere, then $1 / f \in \mathcal{A} ^ { * }$).
The space ${\cal P M} ^ { * }$ of all sequences $d = \{ d_{ k } \} ^ { \infty } _ { k = - \infty}$ with finite norm
\begin{equation*} \| d \| _ {\cal P M ^* } = \operatorname { sup } _ { n \geq 0 } \frac { 1 } { n + 1 } \sum _ { k = - n } ^ { n } | d _ { k } | \end{equation*}
is the dual space of $\mathcal{A} ^ { * }$.
The space ${\cal P M} ^ { * }$ is not separable (cf. also Separable space) and thus the space $\mathcal{A} ^ { * }$, like $\mathcal{A}$, is not reflexive (cf. also Reflexive space).
Spectral properties of $\mathcal{A} ^ { * }$.
The following two results are analogues for $\mathcal{A} ^ { * }$ of the Herz theorem and of the Wiener–Ditkin theorem, respectively.
Let $f _ { N }$ be a function coinciding with $f$ at each point $2 \pi k / N$, where $k , N > 0$ are integers, $k < N$, and $f _ { N }$ is linear on intervals. Suppose $f \in \mathcal{A} ^ { * }$. Then
\begin{equation*} \operatorname { lim } _ { N \rightarrow \infty } \| f - f _ { N } \| _ { \cal A ^ { * } }= 0. \end{equation*}
Let $\Delta _ { \varepsilon } ( t ) = ( 1 - | t | / \varepsilon ) _ { + }$ for $t | \leq \pi$ and $\varepsilon \in ( 0 , \pi / 2 )$, $\Delta _ { \varepsilon } ( t + 2 \pi ) = \Delta _ { \varepsilon } ( t )$, and $V _ { \varepsilon } = 2 \Delta _ { 2 \varepsilon} - \Delta _ { \varepsilon }$. Let $f \in \mathcal{A} ^ { * }$ and $f ( 0 ) = 0$. Then
\begin{equation*} \operatorname { lim } _ { \varepsilon \rightarrow 0 } \| f V _ { \varepsilon } \| _ { \mathcal{A} } * = 0. \end{equation*}
Synthesis problems.
Writing $f \in S$ if $f$ admits synthesis in the norm of $\mathcal{A} ^ { * }$ (cf. also Synthesis problems), for $f \in \mathcal{A} ^ { * }$ the following statements hold.
a) If $f \in \operatorname { Lip } 1$, then $f \in S$ ($\operatorname { Lip } ( 1 / 2 )$ for $\mathcal{A}$).
b) If $f$ is absolutely continuous and in $\operatorname { Lip } \alpha$, $\alpha > 1 / 2$, then $f \in S$ (for $f \in \mathcal{A}$, $f$ has to be of bounded variation).
(Here, analogous conditions for $\mathcal{A}$ are given in parentheses; these assertions make up the Beurling–Pollard theorem.)
The following statements describe structural properties of functions in $\mathcal{A} ^ { * }$. In the sequel, $\omega ( g , .)_p$ stands for the modulus of continuity, in the norm of $L ^ { p }$, of a function $g$ (cf. also Continuity, modulus of).
i) $B _ { 1,1 } ^ { 1 } \subset \mathcal{A} ^ { * } \subset B _ { 2,1 } ^ { 1 / 2 }$, and the imbeddings into these Besov spaces (cf. also Nikol'skii space and Hankel operator) are both continuous.
ii) If $f$ is absolutely continuous and
\begin{equation*} \int _ { 0 } ^ { 1 } \omega ( f ^ { \prime } ; t ) _ { p } \left( \operatorname { ln } \frac { 1 } { t } \right) ^ { - 1 / p ^ { \prime } } t ^ { - 1 } d t < \infty \end{equation*}
for some $p \in [ 1,2 ]$, $p ^ { \prime } = p / ( p - 1 )$, then $f \in \mathcal{A} ^ { * }$.
iii) There exists a continuously differentiable function $f \notin \mathcal{A} ^ { * }$ for which
\begin{equation*} \omega ( f ^ { \prime } ; t ) _ { \infty } = O \left( \left( \operatorname { ln } \frac { 1 } { t } \right) ^ { - 1 / 2 } \right). \end{equation*}
The second inclusion in i) is sharp; indeed, for each $\varepsilon > 0$ there exists a function $f \notin B _ { 2 , \infty } ^ { \varepsilon + 1 / 2 }$ such that $f \in \mathcal{A} ^ { * }$. As for ii), it is sharp for $p = 1$. The question is open for $p > 1$ (as of 2000).
There exists a function $f \in \mathcal{A} ^ { * }$ that is not of bounded variation (cf. also Function of bounded variation).
The following condition, although being very simple, is surprisingly sharp. If $f ^ { \prime } \in \mathcal{A}$, then $f \in \mathcal{A} ^ { * }$. If the Fourier series of $f$ is lacunary in the sense of Hadamard (cf. also Lacunary sequence), then the converse statement holds.
Note that the central problem of spectral synthesis, that is, existence of sets that are not of synthesis as well as existence of functions not admitting synthesis, is still open (as of 2000) for $\mathcal{A} ^ { * }$.
Another open question is connected with Beurling's initial result. It would be interesting to know whether the following statement, converse to that given above, is true or not: If for every $f \in \mathcal{A} ^ { * }$ one has $F \circ f \in \mathcal{A}$, then $F \in \operatorname { Lip } 1$.
Some of the results known for $\mathcal{A} ^ { * }$ have been generalized to the multi-dimensional case.
References
| [a1] | E. Belinsky, E. Liflyand, R. Trigub, "The Banach algebra $A ^ { * }$ and its properties" J. Fourier Anal. Appl. , 3 (1997) pp. 103–129 |
| [a2] | A. Beurling, "On the spectral synthesis of bounded functions" Acta Math. , 81 (1949) pp. 225–238 |
| [a3] | J.-P. Kahane, "Séries de Fourier absolument convergentes" , Springer (1970) |
Beurling algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Beurling_algebra&oldid=50474