Beta-function
From Encyclopedia of Mathematics
 -function, Euler
-function, Euler  -function, Euler integral of the first kind
-function, Euler integral of the first kind
A function of two variables  and
and  which, for
which, for  , is defined by the equation
, is defined by the equation
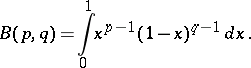 | (*) |
The values of the beta-function for various values of the parameters 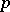 and
and 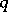 are connected by the following relationships:
are connected by the following relationships:
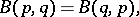 |
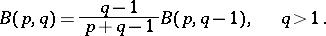 |
The following formula is valid:
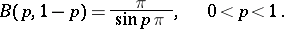 |
If 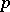 and
and 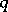 are complex, the integral (*) converges if
are complex, the integral (*) converges if 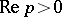 and
and 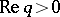 . The beta-function can be expressed by the gamma-function:
. The beta-function can be expressed by the gamma-function:
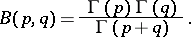 |
How to Cite This Entry:
Beta-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Beta-function&oldid=14450
Beta-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Beta-function&oldid=14450
This article was adapted from an original article by V.I. Bityutskov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article