Bessel equation
A second-order linear ordinary differential equation
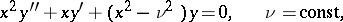 | (1) |
or, in self-adjoint form:
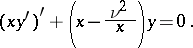 |
The number  is called the order of the Bessel equation; in the general case
is called the order of the Bessel equation; in the general case 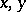 and
and  assume complex values. The substitution
assume complex values. The substitution 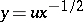 yields the reduced form of equation (1):
yields the reduced form of equation (1):
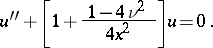 | (2) |
A Bessel equation is a special case of a confluent hypergeometric equation; if 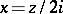 is substituted into (2), equation (2) becomes a Whittaker equation. In equation (1) the point
is substituted into (2), equation (2) becomes a Whittaker equation. In equation (1) the point 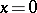 is weakly singular, while the point
is weakly singular, while the point 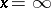 is strongly singular. For this reason a Bessel equation does not belong to the class of Fuchsian equations (cf. Fuchsian equation). F. Bessel [1] was the first to study equation (1) systematically, but such equations are encountered even earlier in the works of D. Bernoulli, L. Euler and J.L. Lagrange.
is strongly singular. For this reason a Bessel equation does not belong to the class of Fuchsian equations (cf. Fuchsian equation). F. Bessel [1] was the first to study equation (1) systematically, but such equations are encountered even earlier in the works of D. Bernoulli, L. Euler and J.L. Lagrange.
A Bessel equation results from separation of variables in many problems of mathematical physics [2], particularly in the case of boundary value problems of potential theory for a cylindrical domain.
The solutions of Bessel equations are called cylinder functions (or Bessel functions). These may be subdivided into the cylinder functions of the first kind (Bessel functions) 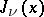 , the cylinder functions of the second kind (Weber functions or Neumann functions, (cf. Weber function; Neumann function)
, the cylinder functions of the second kind (Weber functions or Neumann functions, (cf. Weber function; Neumann function) 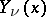 and the cylinder functions of the third kind (Hankel functions)
and the cylinder functions of the third kind (Hankel functions) 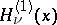 ,
, 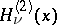 . If the order
. If the order  is fixed, all these functions are analytic functions of the complex argument
is fixed, all these functions are analytic functions of the complex argument  ; for all these functions, except for the functions
; for all these functions, except for the functions 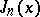 of integer order, the point
of integer order, the point 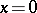 is a branch point. If the argument
is a branch point. If the argument  is fixed, all these functions are single-valued entire functions of the complex order
is fixed, all these functions are single-valued entire functions of the complex order  [3].
[3].
If the order  is not an integer, then the general solution of equation (1) may be written as
is not an integer, then the general solution of equation (1) may be written as
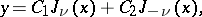 |
where 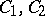 are arbitrary constants. For a given order, any two of the functions
are arbitrary constants. For a given order, any two of the functions 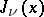 ,
, 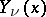 ,
, 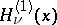 ,
, 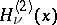 are linearly independent and may serve as a fundamental system of solutions of (1). For this reason, the general solution of equation (1) can be represented, in particular, in the following forms:
are linearly independent and may serve as a fundamental system of solutions of (1). For this reason, the general solution of equation (1) can be represented, in particular, in the following forms:
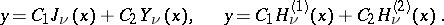 |
The following equations are closely connected with equation (1): the equation
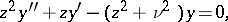 |
which becomes (1) as a result of the substitution 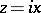 , and with as a fundamental system of solutions the modified cylinder functions (Bessel functions of imaginary argument), and the equation
, and with as a fundamental system of solutions the modified cylinder functions (Bessel functions of imaginary argument), and the equation
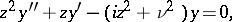 |
which becomes equation (1) as a result of the substitution 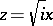 and which has the Kelvin functions as its fundamental system of solutions. Many other second-order linear ordinary differential equations (e.g. the Airy equation) can also be transformed into equation (1) by a transformation of the unknown function and the independent variable. The solution of a series of linear equations of higher orders may be written in the form of Bessel functions [4].
and which has the Kelvin functions as its fundamental system of solutions. Many other second-order linear ordinary differential equations (e.g. the Airy equation) can also be transformed into equation (1) by a transformation of the unknown function and the independent variable. The solution of a series of linear equations of higher orders may be written in the form of Bessel functions [4].
The substitution 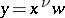 transforms (1) into the Laplace equation:
transforms (1) into the Laplace equation:
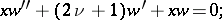 |
which permits one to represent the solutions of (1) by contour integrals in the complex plane.
In applications it is often required to find the eigen values of the equation
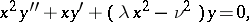 | (3) |
where  is fixed while
is fixed while 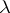 is a parameter. Equation (3) on the segment
is a parameter. Equation (3) on the segment 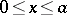 with the boundary conditions:
with the boundary conditions:
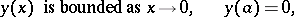 |
is an example of a problem with a discrete spectrum (the eigen values are determined by the condition 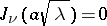 in terms of the zeros of a Bessel function). Equation (3) with the boundary condition:
in terms of the zeros of a Bessel function). Equation (3) with the boundary condition:
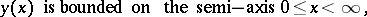 |
represents a problem with a continuous spectrum (eigen values 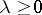 ).
).
The inhomogeneous Bessel equation
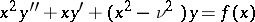 | (4) |
has the particular solution
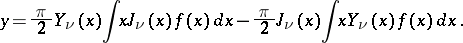 |
Solutions of equation (4) have been studied in more detail for a right-hand side of special form. Thus, if 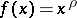 , equation (4) is satisfied by a Lommel function; if
, equation (4) is satisfied by a Lommel function; if
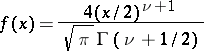 |
it is satisfied by a Struve function; if
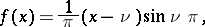 |
it is satisfied by an Anger function; and if
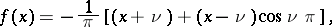 |
it is satisfied by a Weber function.
There are linear equations of higher orders with solutions whose properties are analogous to those of Bessel functions. The general  -th order equation of Bessel type has the form
-th order equation of Bessel type has the form
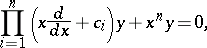 |
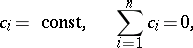 |
and its solution depends on 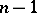 parameters. In particular, a third-order equation of Bessel type (which has a solution with two parameters
parameters. In particular, a third-order equation of Bessel type (which has a solution with two parameters 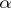 ,
, 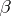 ) may be represented in the form:
) may be represented in the form:
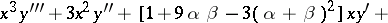 |
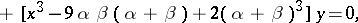 |
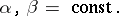 |
References
| [1] | F. Bessel, Abh. d. K. Akad. Wiss. Berlin (1824) pp. 1–52 |
| [2] | A. Gray, G.B. Mathews, "A treatise on Bessel functions and their application to physics" , Macmillan (1931) |
| [3] | G.N. Watson, "A treatise on the theory of Bessel functions" , 1–2 , Cambridge Univ. Press (1952) |
| [4] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1971) |
Comments
References
| [a1] | N.N. Lebedev, "Special functions and their applications" , Dover, reprint (1972) (Translated from Russian) |
Bessel equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bessel_equation&oldid=14419