Bernstein interpolation method
A sequence of algebraic polynomials converging uniformly on  to a function
to a function  that is continuous on this interval. More precisely, Bernstein's interpolation method is a sequence of algebraic polynomials
that is continuous on this interval. More precisely, Bernstein's interpolation method is a sequence of algebraic polynomials
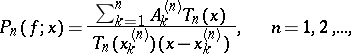 |
where the
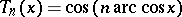 |
are the Chebyshev polynomials; the
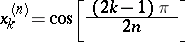 |
are the interpolation nodes; and
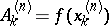 |
if  is an arbitrary positive integer,
is an arbitrary positive integer,  ,
,  ,
,  ,
,  otherwise
otherwise
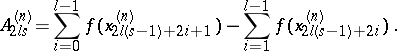 |
The ratio between the degree of the polynomial 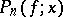 and the number of points at which
and the number of points at which 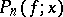 equals
equals  is
is 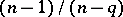 , which tends to
, which tends to 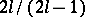 as
as 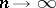 ; if
; if  is sufficiently large, this limit is arbitrary close to one. The method was introduced by S.N. Bernstein [S.N. Bernshtein] in 1931 [1].
is sufficiently large, this limit is arbitrary close to one. The method was introduced by S.N. Bernstein [S.N. Bernshtein] in 1931 [1].
References
| [1] | S.N. Bernshtein, , Collected works , 2 , Moscow (1954) pp. 130–140 (In Russian) |
Comments
This method of interpolation seems not very well known in the West. There is, however, a well-known method of Bernstein that uses the special interpolation nodes 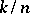 ,
,  , for bounded functions on
, for bounded functions on  . This method is given by the Bernstein polynomials. The sequence of Bernstein polynomials
. This method is given by the Bernstein polynomials. The sequence of Bernstein polynomials 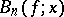 constructed for a bounded function
constructed for a bounded function 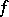 on
on  converges to
converges to  at each point of continuity
at each point of continuity  of
of 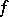 . If
. If 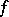 is continuous on
is continuous on  , the sequence converges uniformly (to
, the sequence converges uniformly (to  ) on
) on 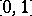 . If
. If 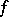 is differentiable,
is differentiable,  (at each point of continuity of
(at each point of continuity of  ), cf [a1].
), cf [a1].
This method of Bernstein is often used to prove the Weierstrass theorem (on approximation). For a generalization of the method (the monotone-operator theorem), see [a2], Chapt. 3, Sect. 3. See also Approximation of functions, linear methods.
References
| [a1] | P.J. Davis, "Interpolation and approximation" , Dover, reprint (1975) |
| [a2] | E.W. Cheney, "Introduction to approximation theory" , Chelsea, reprint (1982) pp. 203ff |
Bernstein interpolation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernstein_interpolation_method&oldid=11602