Beilinson conjectures
Let 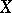 be a smooth projective variety (cf. Projective scheme) defined over
be a smooth projective variety (cf. Projective scheme) defined over 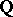 . For such
. For such 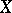 one has, on the one hand, the algebraic
one has, on the one hand, the algebraic 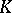 -groups (cf.
-groups (cf. 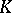 -theory)
-theory) 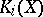 ,
, 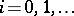 , and on the other hand, various cohomology theories, such as Betti cohomology
, and on the other hand, various cohomology theories, such as Betti cohomology 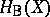 , de Rham cohomology
, de Rham cohomology 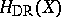 and
and 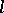 -adic cohomology
-adic cohomology 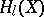 . These cohomology theories can be considered as realizations of the (Chow) motive
. These cohomology theories can be considered as realizations of the (Chow) motive 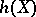 associated to
associated to 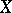 . There are comparison isomorphisms between them. Decomposing the motive
. There are comparison isomorphisms between them. Decomposing the motive 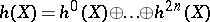 ,
, 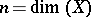 , one may fix
, one may fix 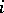 ,
, 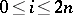 , and define, via the Frobenius action on
, and define, via the Frobenius action on 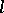 -adic cohomology
-adic cohomology 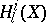 (cf. [a6]), the
(cf. [a6]), the 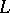 -function
-function 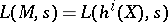 , an infinite product which converges absolutely for
, an infinite product which converges absolutely for 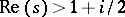 . Here,
. Here, 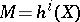 is a pure motive of weight
is a pure motive of weight  . Using the Hodge structure on the cohomology
. Using the Hodge structure on the cohomology 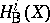 of the complex manifold
of the complex manifold 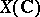 , one defines the
, one defines the 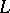 -factor "at infinity" ,
-factor "at infinity" , 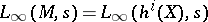 , essentially as a product of
, essentially as a product of 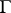 -factors. Finally, one defines
-factors. Finally, one defines 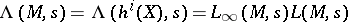 . For
. For  one has a conjectural analytic continuation and functional equation
one has a conjectural analytic continuation and functional equation 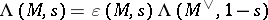 , for a suitable function
, for a suitable function 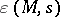 of the form
of the form 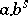 , and with
, and with 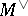 the dual motive of
the dual motive of 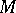 . Here, by Poincaré duality and hard Lefschetz, this means
. Here, by Poincaré duality and hard Lefschetz, this means 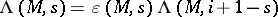 . In general, for an arbitrary motive
. In general, for an arbitrary motive 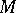 of pure weight
of pure weight 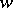 , one extends the above construction of
, one extends the above construction of 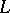 ,
, 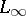 and
and 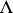 . One should have
. One should have 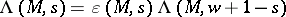 .
.
On the 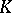 -groups of
-groups of 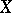 one has the action of the Adams operators
one has the action of the Adams operators 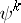 (cf. Cohomology operation). They all commute with each other. Write
(cf. Cohomology operation). They all commute with each other. Write 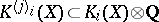 for the subspace on which
for the subspace on which 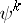 acts as multiplication by
acts as multiplication by  ,
, 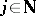 . A. Beilinson defines the absolute or motivic cohomology
. A. Beilinson defines the absolute or motivic cohomology  . As a matter of fact, this can be defined for any regular or affine (simplicial) scheme
. As a matter of fact, this can be defined for any regular or affine (simplicial) scheme 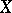 . It has many nice properties of a cohomology theory; in particular there is a motivic Chern character mapping (a sum of projections after tensoring with
. It has many nice properties of a cohomology theory; in particular there is a motivic Chern character mapping (a sum of projections after tensoring with 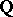 )
) 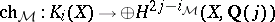 . A classical theorem of A. Grothendieck says that
. A classical theorem of A. Grothendieck says that 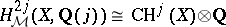 . Beilinson has extended motivic cohomology to the category of (Chow) motives with coefficients in a number field
. Beilinson has extended motivic cohomology to the category of (Chow) motives with coefficients in a number field 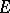 . Assuming that
. Assuming that 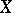 admits a regular model
admits a regular model 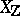 over
over 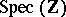 , one defines
, one defines
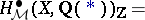 |
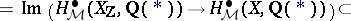 |
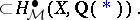 |
This is independent of the regular model, provided that it exists. The 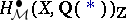 are conjectured to be finite-dimensional. Their construction may be applied to define groups
are conjectured to be finite-dimensional. Their construction may be applied to define groups 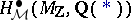 for any Chow motive
for any Chow motive 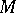 over
over 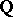 with coefficients in
with coefficients in 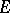 .
.
Another main ingredient of Beilinson's conjectures is Deligne (or Deligne–Beilinson) cohomology. This is defined for any quasi-projective variety (cf. Quasi-projective scheme) 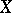 defined over the complex numbers. For smooth projective
defined over the complex numbers. For smooth projective 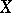 it is easy to define. Let
it is easy to define. Let 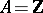 ,
, 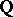 or
or 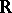 and write
and write 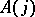 for the subgroup
for the subgroup 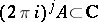 , where
, where  . Consider the following complex of sheaves on
. Consider the following complex of sheaves on  :
:
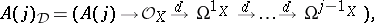 |
where 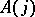 (respectively,
(respectively,  ) is placed in degree
) is placed in degree  (respectively,
(respectively, 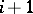 ).
). 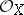 (respectively,
(respectively, 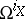 ) denotes the sheaf of holomorphic functions (respectively, holomorphic
) denotes the sheaf of holomorphic functions (respectively, holomorphic 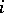 -forms) on
-forms) on 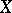 . One defines the Deligne cohomology of
. One defines the Deligne cohomology of 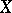 as
as
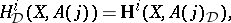 |
the hypercohomology of the complex 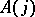 . For arbitrary
. For arbitrary  one uses a smooth compactification
one uses a smooth compactification 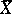 of
of 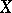 such that
such that 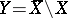 is a normal crossings divisor, and, using the associated logarithmic de Rham complex of
is a normal crossings divisor, and, using the associated logarithmic de Rham complex of 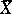 along
along 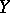 , it is possible to construct well-defined Deligne–Beilinson cohomology
, it is possible to construct well-defined Deligne–Beilinson cohomology 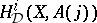 . Thus, one obtains a good cohomology theory, with supports, Poincaré duality, even a homological counterpart, satisfying the axioms of a Poincaré duality theory in the sense of S. Bloch and A. Ogus. In particular, there is again a Chern character mapping
. Thus, one obtains a good cohomology theory, with supports, Poincaré duality, even a homological counterpart, satisfying the axioms of a Poincaré duality theory in the sense of S. Bloch and A. Ogus. In particular, there is again a Chern character mapping 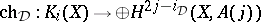 . For smooth projective
. For smooth projective 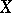 defined over
defined over 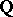 , one defines
, one defines 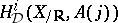 as the subspace of
as the subspace of 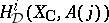 invariant under the induced action of complex conjugation
invariant under the induced action of complex conjugation 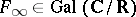 acting on the pair
acting on the pair 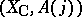 , i.e., acting on differential forms by
, i.e., acting on differential forms by 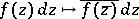 . Similarly for
. Similarly for 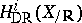 and
and 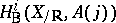 . Then, for an integer
. Then, for an integer 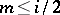 , there is a short exact sequence
, there is a short exact sequence
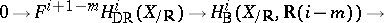 |
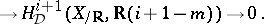 |
The 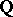 -structures on the first two terms give rise to a natural
-structures on the first two terms give rise to a natural 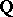 -structure
-structure
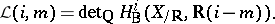 |
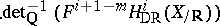 |
on 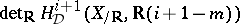 . In the general case of motives with coefficients in
. In the general case of motives with coefficients in 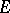 , one will have
, one will have 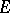 -structures, etc.
-structures, etc.
Taking things together, one sees that, for varieties over 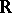 , there are natural transformations, called regulators,
, there are natural transformations, called regulators, 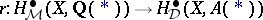 . Already the simplest explicit examples suggest one should restrict to "integral motivic cohomology" and one is led to Beilinson's regulator mappings
. Already the simplest explicit examples suggest one should restrict to "integral motivic cohomology" and one is led to Beilinson's regulator mappings 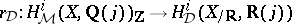 . It should be remarked that one can extend the formalism to the category of Chow motives
. It should be remarked that one can extend the formalism to the category of Chow motives 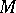 over
over 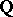 with field of coefficients in the number field
with field of coefficients in the number field 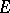 . The
. The 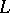 -functions will take their values in
-functions will take their values in 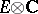 and the regulator mappings will be of the form
and the regulator mappings will be of the form 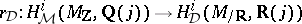 . This is even expected to work for Grothendieck motives, i.e., motives modulo homological (which, conjecturally, coincides with numerical) equivalence.
. This is even expected to work for Grothendieck motives, i.e., motives modulo homological (which, conjecturally, coincides with numerical) equivalence.
Beilinson's first conjecture.
To state Beilinson's conjectures on special values of 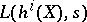 at integer arguments
at integer arguments 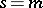 , one distinguishes between three cases:
, one distinguishes between three cases:
i) 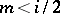 , which by the functional equation corresponds to the region of absolute convergence;
, which by the functional equation corresponds to the region of absolute convergence;
ii) 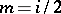 ,
, 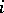 even, which lies on the boundary of the critical strip
even, which lies on the boundary of the critical strip 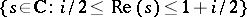 ;
;
iii) 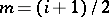 ,
, 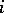 odd, the centre of the critical strip. It is easily shown that
odd, the centre of the critical strip. It is easily shown that 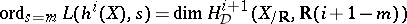 , for
, for 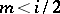 .
.
Beilinson's first conjecture reads as follows. Assume 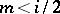 . Then:
. Then: 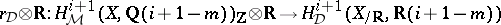 is an isomorphism; and
is an isomorphism; and
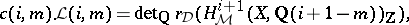 |
where 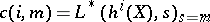 is the first non-vanishing coefficient of the Taylor series expansion of
is the first non-vanishing coefficient of the Taylor series expansion of 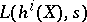 at
at 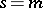 .
.
In [a1], Beilinson states this conjecture for general Chow motives with coefficients in 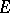 .
.
Some special cases are as follows.
a) For 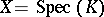 ,
, 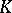 a number field, and
a number field, and 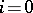 , one recovers the situation studied by A. Borel [a4]. Beilinson showed that his regulator coincides with Borel's regulator (at least modulo
, one recovers the situation studied by A. Borel [a4]. Beilinson showed that his regulator coincides with Borel's regulator (at least modulo 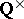 ). Thus, by Borel's results, the first conjecture is true. Classically, for
). Thus, by Borel's results, the first conjecture is true. Classically, for 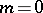 one obtains the Dirichlet regulator and Dedekind's class number formula.
one obtains the Dirichlet regulator and Dedekind's class number formula.
b) Bloch and Beilinson were the first to construct a regulator mapping 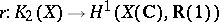 (or even
(or even 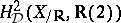 ) for a Riemann surface
) for a Riemann surface 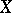 , and make a conjecture about
, and make a conjecture about  . For
. For 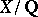 an elliptic curve without complex multiplication,
an elliptic curve without complex multiplication, 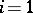 and
and 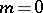 , Bloch and D. Grayson made computer calculations which actually gave rise to a formulation of the first conjecture in terms of the integral model
, Bloch and D. Grayson made computer calculations which actually gave rise to a formulation of the first conjecture in terms of the integral model 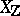 . For elliptic curves with complex multiplication a weak form of the first conjecture was proved by Bloch and Beilinson.
. For elliptic curves with complex multiplication a weak form of the first conjecture was proved by Bloch and Beilinson.
c) Another conjecture which motivated Beilinson's first conjecture is due to P. Deligne [a6]. It is stated in terms of motives and predicts that the 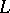 -function of such a motive (cf. also Motives, theory of) at a so-called critical value of the argument would be equal (modulo
-function of such a motive (cf. also Motives, theory of) at a so-called critical value of the argument would be equal (modulo 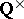 ) to a well-defined period.
) to a well-defined period.
d) J.-F. Mestre and N. Schappacher gave numerical evidence for the case of the symmetric square of an elliptic curve without complex multiplication.
e) For Dirichlet motives, Beilinson proved the conjecture. For general Artin motives one recovers Gross' conjecture.
f) C. Deninger has obtained results for motives of Hecke characters of imaginary quadratic number fields.
g) Beilinson has proved partial results for (products of) modular curves.
h) K.-I. Kimura has given numerical evidence for (a projective curve related to) the Fermat curve 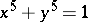 .
.
Some further examples are known. They all deal with modular curves, Shimura curves, products of such curves, Hilbert modular surfaces, or products of elliptic modular surfaces. A general phenomenon occurs: in all these examples there exists a subspace of 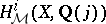 giving rise, via the regulator mapping
giving rise, via the regulator mapping 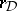 , to a
, to a 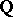 -structure on the corresponding Deligne–Beilinson cohomology with
-structure on the corresponding Deligne–Beilinson cohomology with 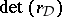 equal (up to a non-zero rational number) to the first non-vanishing coefficient of the
equal (up to a non-zero rational number) to the first non-vanishing coefficient of the 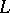 -function at a suitable integer value of its argument.
-function at a suitable integer value of its argument.
Beilinson's second conjecture.
The second conjecture takes into account the possible pole of 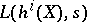 at the Tate point
at the Tate point 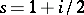 . One shows that
. One shows that
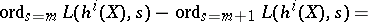 |
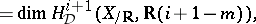 |
for 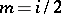 .
.
Beilinson's second conjecture reads as follows. Let  be even and write
be even and write 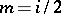 . Then:
. Then:
i) 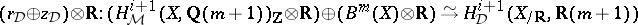 , where
, where 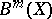 is the group of
is the group of 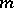 -codimensional algebraic cycles on
-codimensional algebraic cycles on 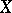 modulo homological equivalence, i.e., the image of the morphism
modulo homological equivalence, i.e., the image of the morphism 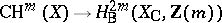 , and
, and 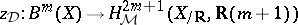 is the inclusion;
is the inclusion;
ii) 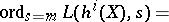
 .
.
iii) 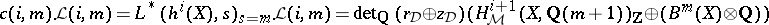 .
.
This conjecture can also be stated in terms of motives.
a) For Artin motives it gives Stark's conjecture.
b) For a Hilbert modular surface 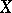 , D. Ramakrishnan proved the existence of a subspace
, D. Ramakrishnan proved the existence of a subspace 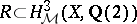 such that
such that
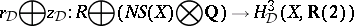 |
gives a 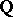 -structure on Deligne cohomology with
-structure on Deligne cohomology with 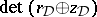 equal (up to a non-zero rational number) to
equal (up to a non-zero rational number) to 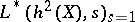 .
.
Beilinson's third conjecture.
The third conjecture deals with the centre 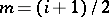 ,
, 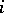 odd, of the critical strip. Let
odd, of the critical strip. Let 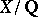 be a smooth projective variety (cf. Projective scheme) of dimension
be a smooth projective variety (cf. Projective scheme) of dimension  , and assume that
, and assume that 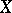 admits a regular, proper model
admits a regular, proper model 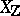 over
over 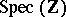 . One has an isomorphism
. One has an isomorphism
 |
giving a period matrix 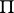 . Let
. Let 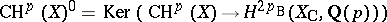 . Beilinson [a3] showed that there exists a unique bilinear pairing
. Beilinson [a3] showed that there exists a unique bilinear pairing 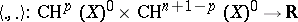 of an arithmetic nature, i.e., closely related to the Gillet–Soulé arithmetic intersection pairing (on
of an arithmetic nature, i.e., closely related to the Gillet–Soulé arithmetic intersection pairing (on 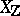 ), and generalizing Arakelov's intersection pairing on arithmetic surfaces.
), and generalizing Arakelov's intersection pairing on arithmetic surfaces.
Beilinson's third conjecture reads as follows. Let 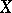 be a smooth projective variety defined over
be a smooth projective variety defined over 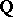 , and assume that
, and assume that 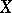 has a regular, proper model
has a regular, proper model 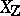 over
over 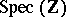 . Let
. Let 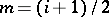 . Then:
. Then:
i) 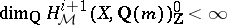 ;
;
ii) the pairing 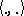 is non-degenerate.
is non-degenerate.
iii) 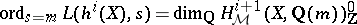 .
.
iv) 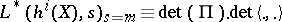 modulo
modulo 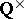 .
.
For 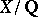 an elliptic curve,
an elliptic curve, 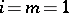 , one recovers the Mordell–Weil theorem and the Birch–Swinnerton-Dyer conjectures for
, one recovers the Mordell–Weil theorem and the Birch–Swinnerton-Dyer conjectures for 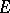 .
.
Generalizations.
Deligne observed that, for 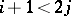 , one can interprete
, one can interprete 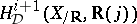 as a Yoneda extension
as a Yoneda extension 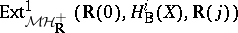 , where
, where 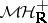 is the category of
is the category of 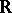 -mixed Hodge structures with a real Frobenius. This made the search for a category of "mixed motives" over
-mixed Hodge structures with a real Frobenius. This made the search for a category of "mixed motives" over 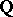 ,
, 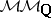 (or, even better, over
(or, even better, over 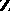 ,
, 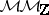 ) very tempting. The regulator mapping in this setting would be just the Betti realization functor
) very tempting. The regulator mapping in this setting would be just the Betti realization functor
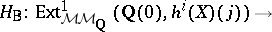 |
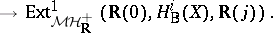 |
The category 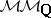 should contain Grothendieck's category of pure motives
should contain Grothendieck's category of pure motives 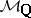 and allow the treatment of arbitrary varieties over
and allow the treatment of arbitrary varieties over 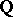 . Analogously, for other base fields
. Analogously, for other base fields 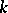 , one should have categories
, one should have categories 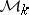 ,
, 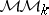 , etc. Also, the role of the Chow groups in the theory of Grothendieck motives might be enlarged to include all the algebraic
, etc. Also, the role of the Chow groups in the theory of Grothendieck motives might be enlarged to include all the algebraic 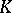 -groups of the variety. In this respect one may mention a very geometric construction by Bloch of generalized Chow groups
-groups of the variety. In this respect one may mention a very geometric construction by Bloch of generalized Chow groups 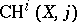 . For
. For 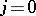 they coincide with
they coincide with 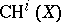 . They are integrally defined and satisfy
. They are integrally defined and satisfy 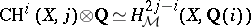 . A series of other conjectures, mainly about filtrations on Chow groups (Beilinson, J.P. Murre), emerges, and the ultimate formulation of Beilinson's conjectures appears in terms of derived categories, mixed motivic sheaves, mixed perverse sheaves, etc., cf. [a3], [a8].
. A series of other conjectures, mainly about filtrations on Chow groups (Beilinson, J.P. Murre), emerges, and the ultimate formulation of Beilinson's conjectures appears in terms of derived categories, mixed motivic sheaves, mixed perverse sheaves, etc., cf. [a3], [a8].
In [a2], Beilinson introduced the notion of absolute Hodge cohomology 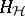 . This generalizes Deligne–Beilinson cohomology by taking the weight filtration into account. It is a derived functor cohomology defined for any scheme
. This generalizes Deligne–Beilinson cohomology by taking the weight filtration into account. It is a derived functor cohomology defined for any scheme 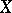 over
over 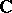 . For
. For 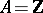 ,
, 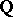 or
or 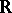 , let
, let 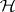 denote the category of
denote the category of 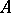 -mixed Hodge structures. In this setting, for
-mixed Hodge structures. In this setting, for 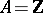 , one can define the Abel–Jacobi mappings of
, one can define the Abel–Jacobi mappings of 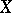 as
as 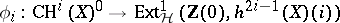 . For smooth projective
. For smooth projective 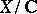 this gives the classical Abel–Jacobi mappings
this gives the classical Abel–Jacobi mappings 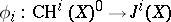 , where
, where 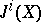 is Griffiths' intermediate Jacobian.
is Griffiths' intermediate Jacobian.
The following conjecture generalizes the classical Hodge conjecture. In this form it is due to Beilinson and U. Jannsen.
The Beilinson–Jannsen conjecture. Let 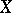 be a smooth variety defined over
be a smooth variety defined over 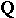 . Then, for all
. Then, for all  , the regulator mapping
, the regulator mapping 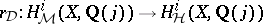 has dense image.
has dense image.
In [a5] there is a formulation of Beilinson's conjectures in terms of (mixed) motives, without the modulo 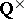 ambiguity. There is also a very precise conjecture in terms of Tamagawa numbers, cf. [a5], [a7] and the contribution by J.-M. Fontaine and B. Perrin-Riou in [a8].
ambiguity. There is also a very precise conjecture in terms of Tamagawa numbers, cf. [a5], [a7] and the contribution by J.-M. Fontaine and B. Perrin-Riou in [a8].
References
| [a1] | A. Beilinson, "Higher regulators and values of 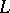 -functions" J. Soviet Math. , 30 (1985) pp. 2036–2070 (In Russian) -functions" J. Soviet Math. , 30 (1985) pp. 2036–2070 (In Russian) |
| [a2] | A. Beilinson, "Notes on absolute Hodge cohomology" , Contemp. Math. , 55 , Amer. Math. Soc. (1985) pp. 35–68 |
| [a3] | A. Beilinson, "Height pairings for algebraic cycles" , Lecture Notes in Mathematics , 1289 , Springer (1987) pp. 1–26 |
| [a4] | A. Borel, "Cohomologie de 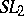 et valeurs de fonctions zeta aux points entiers" Ann. Sci. Pisa (1976) pp. 613–636 et valeurs de fonctions zeta aux points entiers" Ann. Sci. Pisa (1976) pp. 613–636 |
| [a5] | S. Bloch, K. Kato, "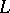 -functions and Tamagawa numbers of motives" , The Grothendieck Festschrift I , Progress in Mathematics , 86 , Birkhäuser (1990) pp. 333–400 -functions and Tamagawa numbers of motives" , The Grothendieck Festschrift I , Progress in Mathematics , 86 , Birkhäuser (1990) pp. 333–400 |
| [a6] | P. Deligne, "Valeurs de fonctions 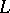 et périodes d'intégrales" , Proc. Symp. Pure Math. , 33 , Amer. Math. Soc. (1979) pp. 313–346 et périodes d'intégrales" , Proc. Symp. Pure Math. , 33 , Amer. Math. Soc. (1979) pp. 313–346 |
| [a7] | J.-M. Fontaine, B. Perrin-Riou, "Autour des conjectures de Bloch et Kato, I--III" C.R. Acad. Sci. Paris , 313 (1991) pp. 189–196; 349–356; 421–428 |
| [a8] | "Motives" U. Jannsen (ed.) etAAsal. (ed.) , Proc. Symp. Pure Math. , 55 , Amer. Math. Soc. (1994) |
Beilinson conjectures. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Beilinson_conjectures&oldid=24042