Baskakov operators
V.A. Baskakov [a2] introduced a sequence of linear positive operators  with weights
with weights
 |
by
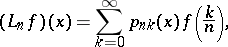 | (a1) |
where  ,
,  ,
,  , for all functions
, for all functions  on
on  for which the series converges. Here,
for which the series converges. Here,  is a sequence of functions defined on
is a sequence of functions defined on  having the following properties for every
having the following properties for every 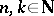 ,
, 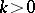 :
:
i) 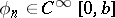 ;
;
ii) 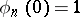 ;
;
iii) 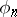 is completely monotone, i.e.,
is completely monotone, i.e.,  ;
;
iv) there exists an integer  such that
such that  ,
,  .
.
Baskakov studied convergence theorems of bounded continuous functions for the operators (a1). For saturation classes for continuous functions with compact support, see [a8]. For a result concerning bounded continuous functions, see [a3].
In his work on Baskakov operators, C.P. May [a6] took conditions slightly different from those mentioned above and showed that the local inverse and saturation theorems hold for functions with growth less than 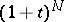 for some
for some  . Bernstein polynomials and Szász–Mirakian operators are the particular cases of Baskakov operators considered by May.
. Bernstein polynomials and Szász–Mirakian operators are the particular cases of Baskakov operators considered by May.
S.P. Singh [a7] studied simultaneous approximation, using another modification of the conditions in the original definition of Baskakov operators. However, it was shown that his result is not correct (cf., e.g., [a1], Remarks).
Motivated by the Durrmeyer integral modification of the Bernstein polynomials, M. Heilmann [a4] modified the Baskakov operators in a similar manner by replacing the discrete values 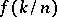 in (a1) by an integral over the weighted function, namely,
in (a1) by an integral over the weighted function, namely,
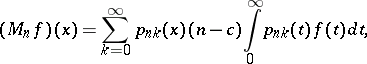 |
 |
where  is a function on
is a function on  for which the right-hand side is defined. He studied global direct and inverse
for which the right-hand side is defined. He studied global direct and inverse  -approximation theorems for these operators.
-approximation theorems for these operators.
Subsequently, a global direct result for simultaneous approximation in the  -metric in terms of the second-order Ditzian–Totik modulus of smoothness was proved, see [a5]. For local direct results for simultaneous approximation of functions with polynomial growth, see [a5].
-metric in terms of the second-order Ditzian–Totik modulus of smoothness was proved, see [a5]. For local direct results for simultaneous approximation of functions with polynomial growth, see [a5].
References
| [a1] | P.N. Agrawal, H.S. Kasana, "On simultaneous approximation by Szász–Mirakian operators" Bull. Inst. Math. Acad. Sinica , 22 (1994) pp. 181–188 |
| [a2] | V.A. Baskakov, "An example of a sequence of linear positive operators in the space of continuous functions" Dokl. Akad. Nauk SSSR , 113 (1957) pp. 249–251 (In Russian) |
| [a3] | H. Berens, "Pointwise saturation of positive operators" J. Approx. Th. , 6 (1972) pp. 135–146 |
| [a4] | M. Heilmann, "Approximation auf  durch das Verfahren der Operatoren vom Baskakov–Durrmeyer Typ" , Univ. Dortmund (1987) (Dissertation) durch das Verfahren der Operatoren vom Baskakov–Durrmeyer Typ" , Univ. Dortmund (1987) (Dissertation) |
| [a5] | M. Heilmann, M.W. Müller, "On simultaneous approximation by the method of Baskakov–Durrmeyer operators" Numer. Funct. Anal. Optim. , 10 (1989) pp. 127–138 |
| [a6] | C.P. May, "Saturation and inverse theorems for combinations of a class of exponential-type operators" Canad. J. Math. , 28 (1976) pp. 1224–1250 |
| [a7] | S.P. Singh, "On Baskakov-type operators" Comment. Math. Univ. St. Pauli, , 31 (1982) pp. 137–142 |
| [a8] | Y. Suzuki, "Saturation of local approximation by linear positive operators of Bernstein type" Tôhoku Math. J. , 19 (1967) pp. 429–453 |
Baskakov operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baskakov_operators&oldid=18362