Difference between revisions of "Banach function space"
(Importing text file) |
(latex details) |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct and if all png images have been replaced by TeX code, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 200 formulas, 198 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|part}} | |
| + | Let $( \Omega , \Sigma , \mu )$ be a complete $\sigma$-finite [[Measure space|measure space]] and let $L ^ { 0 } ( \mu ) = L ^ { 0 } ( \Omega , \Sigma , \mu )$ be the space of all equivalence classes of $\mu$-measurable real-valued functions endowed with the topology of convergence in measure relative to each set of finite measure. | ||
| − | + | A [[Banach space|Banach space]] $X \subset L ^ { 0 } ( \mu )$ is called a Banach function space on $( \Omega , \Sigma , \mu )$ if there exists a $u \in X$ such that $u > 0$ almost everywhere and $X$ satisfies the ideal property: | |
| − | The Lebesgue function spaces | + | \begin{equation*} x \in L ^ { 0 } ( \mu ) , y \in X , | x | \leq | y | \mu - a.e. \end{equation*} |
| + | |||
| + | \begin{equation*} \Downarrow x \in X \text { and } \| x \| \leq \| y \|. \end{equation*} | ||
| + | |||
| + | The Lebesgue function spaces $L _ { p }$ ($1 \leq p \leq \infty$) play a primary role in many problems arising in mathematical analysis. There are other classes of Banach function spaces that are also of interest. The classes of Musielak–Orlicz, Lorentz and Marcinkiewicz spaces, for example, are of intrinsic importance (cf. also [[Orlicz space|Orlicz space]]; [[Orlicz–Lorentz space|Orlicz–Lorentz space]]; [[Marcinkiewicz space|Marcinkiewicz space]]). Function spaces are important and natural examples of abstract Banach lattices (a Banach lattice is a Banach space that is also a [[Vector lattice|vector lattice]] $X$ with the property that $\| x \| \leq \| y \|$ whenever $| x | \leq | y |$, where $| x | = x \vee ( - x )$, cf. also [[Banach lattice|Banach lattice]]). A Banach lattice is said to be order continuous if $\| x _ { n } \| \rightarrow 0$ whenever $x _ { n } \downarrow 0$. The following very useful general representation result (see [[#References|[a12]]]) allows one to reduce most of the proofs for a quite large class of abstract Banach lattices to the case of Banach function spaces: Let $X$ be an order-continuous Banach lattice with a weak unit (a weak unit is an element $e > 0$ such that $e \wedge | x | = 0$ implies $x = 0$). Then there exist a [[Probability space|probability space]] $( \Omega , \Sigma , \mu )$ and a Banach function space $X$ on $( \Omega , \Sigma , \mu )$ such that $X$ is isometrically lattice-isomorphic to $X$ and $L _ { \infty } ( \mu ) \subset X \subset L _ { 1 } ( \mu )$ with continuous inclusions. | ||
See [[#References|[a2]]], [[#References|[a7]]], [[#References|[a10]]], [[#References|[a14]]] for a general theory of Banach lattices. | See [[#References|[a2]]], [[#References|[a7]]], [[#References|[a10]]], [[#References|[a14]]] for a general theory of Banach lattices. | ||
| − | A Banach function space | + | A Banach function space $X$ is said to have the Fatou property if whenever $( f _ { n } )$ is a norm-bounded sequence in $X$ such that $0 \leq f _ { n } \uparrow f \in L ^ { 0 } ( \mu )$, then $f \in X$ and $\| f _ { n } \| \rightarrow \| f \|$. |
| − | In recent (1998) years a great deal of research went into the study of rearrangement-invariant function spaces, in particular of Orlicz spaces. General references to this area are e.g. [[#References|[a7]]], [[#References|[a11]]], [[#References|[a12]]]. A Banach function space | + | In recent (1998) years a great deal of research went into the study of rearrangement-invariant function spaces, in particular of Orlicz spaces. General references to this area are e.g. [[#References|[a7]]], [[#References|[a11]]], [[#References|[a12]]]. A Banach function space $X$ is said to be rearrangement invariant if whenever $f \in X$, $g \in L ^ { 0 } ( \mu )$, and $f$ and $g$ are equi-measurable, then $g \in X$ and $\| f \| = \| g \|$. Two functions $f$ and $g$ are called equi-measurable if $| f|$ and $| g |$ have identical distributions, that is, |
| − | + | \begin{equation*} \mu _ { f } ( \lambda ) = \mu \{ t \in \Omega : | f ( t ) | > \lambda \} = \mu _ { g } ( \lambda ) \end{equation*} | |
| − | for all | + | for all $\lambda > 0$. |
| − | In the study of rearrangement-invariant function spaces, the Boyd indices play an important role (see e.g. [[#References|[a7]]], [[#References|[a12]]], and [[Boyd index|Boyd index]]). The Boyd indices | + | In the study of rearrangement-invariant function spaces, the Boyd indices play an important role (see e.g. [[#References|[a7]]], [[#References|[a12]]], and [[Boyd index|Boyd index]]). The Boyd indices $p_{X} $ and $q_X$ of a rearrangement-invariant function space $X$ on $[0,1]$ or $[ 0 , \infty )$ are defined by |
| − | + | \begin{equation*} p _ { X } = \operatorname { lim } _ { s \rightarrow \infty } \frac { \operatorname { log } s } { \operatorname { log } \| D _ { s } \| _ { X } }, \end{equation*} | |
| − | + | \begin{equation*} q _ { X } = \operatorname { lim } _ { s \rightarrow 0 + } \frac { \operatorname { log } s } { \operatorname { log } \| D _ { s } \| _ { X } }, \end{equation*} | |
| − | where for | + | where for $s > 0$, $D _ { S }$ denotes the dilation operator, defined by $D _ { s } f ( t ) = f ( t / s )$ for $f \in X$ (where $f$ is defined to be zero outside $[0,1]$ in the former case). |
| − | For example, consider the following results, which hold for every separable rearrangement-invariant function space | + | For example, consider the following results, which hold for every separable rearrangement-invariant function space $X$ on $[0,1]$: |
| − | i) | + | i) $X$ has an unconditional basis if and only if $1 < p_{ X}$ and $q_{X} < \infty$ (see, e.g., [[#References|[a11]]], [[#References|[a12]]]); |
| − | ii) if < | + | ii) if $1 < p_{ X}$ and $q_{X} < \infty$, then $X$ is a primary, i.e., whenever $X = E \oplus F$, then at least one of $E$ and $F$ is isomorphic to $X$ (see [[#References|[a3]]]). |
| − | Rearrangement-invariant function spaces play an important role in the theory of [[Interpolation of operators|interpolation of operators]] (see [[#References|[a4]]], [[#References|[a11]]]). A remarkable result of A.P. Calderón [[#References|[a5]]] on the characterization of all interpolation spaces between | + | Rearrangement-invariant function spaces play an important role in the theory of [[Interpolation of operators|interpolation of operators]] (see [[#References|[a4]]], [[#References|[a11]]]). A remarkable result of A.P. Calderón [[#References|[a5]]] on the characterization of all interpolation spaces between $L _ { 1 } = L _ { 1 } ( \mu )$ and $L _ { \infty } = L _ { \infty } ( \mu )$ asserts that $X$ is an interpolation space with respect to the couple $( L _ { 1 } , L _ { \infty } )$ (i.e., that every [[Linear operator|linear operator]] $T : L _ { 1 } + L _ { \infty } \rightarrow L _ { 1 } + L _ { \infty }$ such that $T : L _ { 1 } \rightarrow L _ { 1 }$ and $T : L _ { \infty } \rightarrow L _ { \infty }$ boundedly, also maps $X$ to $X$ boundedly) if and only if it has the following property: For every $g \in X$ and every $f \in L _ { 1 } + L _ { \infty }$, whenever $\int _ { 0 } ^ { t } f ^ { * } ( s ) d s \leq \int _ { 0 } ^ { t } g ^ { * } ( s ) d s$ for all $t > 0$, it follows that $f \in X$ and $\| f \|_X \leq C\| g \|_X$ for some absolute constant $C$. |
| − | Here, | + | Here, $f ^ { * }$ denotes the non-increasing rearrangement of $f$, which is defined by |
| − | + | \begin{equation*} f ^ { * } ( t ) = \operatorname { inf } \{ \lambda > 0 : \mu _ { f } ( \lambda ) \leq t \} \end{equation*} | |
| − | for | + | for $t > 0$. In particular, Calderón's result implies that rearrangement-invariant function spaces which have the Fatou property or are separable are interpolation spaces between $L_1$ and $L _ { \infty }$. |
| − | The Köthe dual space | + | The Köthe dual space $X ^ { \prime }$ of a Banach function space $X$ on $( \Omega , \Sigma , \mu )$ is defined to be the space of all $x ^ { \prime }$ for which $x x ^ { \prime } \in L _ { 1 } ( \mu )$ for each $x \in X$ (cf. also [[Köthe–Toeplitz dual|Köthe–Toeplitz dual]]). The space $X ^ { \prime }$ is a Banach function space endowed with the norm |
| − | + | \begin{equation*} \| x ^ { \prime } \| _ { X ^ { \prime } } = \operatorname { sup } \{ \int _ { \Omega } | x x ^ { \prime } | d \mu : \| x \| _ { X } \leq 1 \}. \end{equation*} | |
| − | Moreover, | + | Moreover, $X ^ { \prime \prime } = X$ isometrically if and only if $X$ has the Fatou property. |
| − | It is important to describe the relation between the Köthe dual | + | It is important to describe the relation between the Köthe dual $X ^ { \prime }$ and the usual (topological) dual space $X ^ { * }$ of a Banach function space $X$. A [[Linear functional|linear functional]] $f$ on $X$ is said to be order continuous (or integral) if $f ( x _ { n } ) \rightarrow 0$ for every sequence $\{ x _ { n } \}$ in $X$ such that $x _ { n } \downarrow 0$ almost everywhere. Let $X ^ { * }_{c}$ be the space all order-continuous functionals. This is a closed and norm-one complemented subspace of $X ^ { * }$. Thus, $X ^ { * } = X _ { c } ^ { * } \oplus X _ { s } ^ { * }$, where $X _ { s } ^ { * }$ denotes a complement to $X ^ { * }_{c}$, called the space of all singular functionals on $X$. The space $X ^ { * }_{c}$ is always total on $X$ (cf. [[Total set|Total set]]). Furthermore, it is norming, i.e., |
| − | + | \begin{equation*} \| x \| _ { X } = \operatorname { sup } \left\{ \left| \int _ { \Omega } x x ^ { \prime } d \mu \right| : x ^ { \prime } \in X ^ { \prime } , \| x ^ { \prime } \| _ { X ^ { \prime } } \leq 1 \right\}, \end{equation*} | |
| − | if and only if the norm on | + | if and only if the norm on $X$ is order semi-continuous, i.e., $\| f _ { n } \| \rightarrow \| f \|$ whenever $0 \leq f _ { n } \uparrow f \in X$. The mapping that assigns to every $x ^ { \prime } \in X ^ { \prime }$ the functional $x \mapsto \int _ { \Omega } x x ^ { \prime } d \mu$ on $X$ is an order-linear isometry from the Köthe dual space $X ^ { \prime }$ onto $X ^ { * }_{c}$. In this way $X ^ { * }_{c}$ is identified with $X ^ { \prime }$. In particular, if $X$ is an order-continuous Banach function space, then $X ^ { * }$ can be identified with $X ^ { \prime }$ (see [[#References|[a10]]], [[#References|[a12]]], [[#References|[a14]]]). |
| − | There are many methods of constructing Banach function spaces which are intermediate in some sense between two given Banach function spaces. One such method is the following construction, again due to Calderón [[#References|[a5]]]. See also [[#References|[a13]]] for the generalized version due to G.A. Lozanovskii. Let | + | There are many methods of constructing Banach function spaces which are intermediate in some sense between two given Banach function spaces. One such method is the following construction, again due to Calderón [[#References|[a5]]]. See also [[#References|[a13]]] for the generalized version due to G.A. Lozanovskii. Let $X _ { 0 }$ and $X _ { 1 }$ be two Banach function spaces on the same measure space $( \Omega , \Sigma , \mu )$. For each $\theta \in ( 0,1 )$, the lattice $X _ { \theta } = X _ { 0 } ^ { 1 - \theta } X _ { 1 } ^ { \theta }$ is defined to be the space of all $x \in L ^ { 0 } ( \mu )$ such that $| x | = | x _ { 0 } | ^ { 1 - \theta } | x _ { 1 } | ^ { \theta }$ $\mu$-almost everywhere for some $x _ { 0 } \in X _ { 0 }$ and $x _ { 1 } \in X _ { 1 }$. The space $X _ { \theta }$ is a Banach function space endowed with the norm |
| − | + | \begin{equation*} \| x \| _ { \theta } = \end{equation*} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b120/b120040/b120040149.png"/></td> </tr></table> |
| − | The identity | + | The identity $( X _ { 0 } ^ { 1 - \theta } X _ { 1 } ^ { \theta } ) ^ { \prime } = ( X _ { 0 } ^ { \prime } ) ^ { 1 - \theta } ( X _ { 1 } ^ { \prime } ) ^ { \theta }$ for all $0 < \theta < 1$ is an important result proved by Lozanovskii [[#References|[a13]]]. Closely related results are the formula $X ^ { 1 / 2 } ( X ^ { \prime } ) ^ { 1 / 2 } = L _ { 2 }$, which holds for any Banach function space on $( \Omega , \Sigma , \mu )$, and also the Lozanovskii factorization theorem: For every $f \in L _ { 1 } ( \mu )$ and $\epsilon > 0$ there exist $x \in X$ and $y \in X ^ { \prime }$ such that $f = x y$ and $\|x \|_X \| y \| _ { X ^ { \prime } } \leq ( 1 + \epsilon ) \| f \| _ { L _ { 1 } }$. If $X$ has the Fatou property, the theorem is true for $\epsilon = 0$ as well. |
This theorem has proved to be very useful in various applications (see, for example, [[#References|[a9]]], [[#References|[a15]]]). | This theorem has proved to be very useful in various applications (see, for example, [[#References|[a9]]], [[#References|[a15]]]). | ||
| − | Calderón's construction has found many other interesting applications in the study of Banach function spaces. An example is Pisier's theorem [[#References|[a16]]], which says that if < | + | Calderón's construction has found many other interesting applications in the study of Banach function spaces. An example is Pisier's theorem [[#References|[a16]]], which says that if $1 < p < 2$, then a Banach function space on $( \Omega , \Sigma , \mu )$ is $p$-convex and $p ^ { \prime }$-concave if and only if $X = ( X _ { 0 } ) ^ { 1 - \theta } ( L _ { 2 } ( \mu ) ) ^ { \theta }$ for some Banach function space $X _ { 0 }$ on $( \Omega , \Sigma , \mu )$, with $\theta = 1 - 1 / p = 1 / p ^ { \prime }$. An application of this result and interpolation yields the following (see [[#References|[a16]]]): Let $X$ be a $p$-convex and $p ^ { \prime }$-concave Banach function space for some $1 < p < 2$. Then every bounded linear operator from an $L_1$-space into $X$ is $( r , 1 )$-summing with $1 / r = 1 / p ^ { \prime } + 1 / 2$, i.e., if $( x _ { n } ) \subset L _ { 1 }$ is such that $\Sigma _ { n = 1 } ^ { \infty } | x ^ { * } ( x _ { n } ) | < \infty$ for all $x ^ { * } \in L _ { \infty }$, then $\Sigma _ { n = 1 } ^ { \infty } \| T _ { x _ { n } } \| _ { X } ^ { r } < \infty$ (cf. also [[Absolutely summing operator|Absolutely summing operator]]). |
| − | For another example see [[#References|[a6]]], where the Calderón construction is used to construct a class of super-reflexive and complementably minimal Banach spaces (i.e., such that every infinite-dimensional closed subspace contains a complemented subspace isomorphic to a given space of this class) which are not isomorphic to | + | For another example see [[#References|[a6]]], where the Calderón construction is used to construct a class of super-reflexive and complementably minimal Banach spaces (i.e., such that every infinite-dimensional closed subspace contains a complemented subspace isomorphic to a given space of this class) which are not isomorphic to $\text{I} _ { p }$ for any $p$. |
| − | One of the most interesting problems in the theory of Banach function spaces is to determine when two Banach function spaces which are isomorphic as Banach spaces are also lattice isomorphic. The first result of this type, due to Y.A. Abramovich and P. Wojtaszczyk [[#References|[a1]]] says that | + | One of the most interesting problems in the theory of Banach function spaces is to determine when two Banach function spaces which are isomorphic as Banach spaces are also lattice isomorphic. The first result of this type, due to Y.A. Abramovich and P. Wojtaszczyk [[#References|[a1]]] says that $L_1$ has a unique structure as a non-atomic Banach function space (i.e., if $X$ is a non-atomic Banach function space isomorphic to $L_1$, then $X$ is lattice isomorphic to $L_1$). The general study of possible rearrangement-invariant lattice structures in Banach function spaces on $[0,1]$ or $[ 0 , \infty )$ was initiated in [[#References|[a7]]], where, among other important results, it is shown that any rearrangement-invariant function space $X$ on $[0,1]$ which is isomorphic to $L _ { p } ( 0,1 )$, $1 \leq p \leq \infty$, is equal to $L _ { p } ( 0,1 )$ up to an equivalent renorming. See also [[#References|[a8]]], where important general results on the uniqueness of the structure of Banach function spaces are presented. |
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> Y.A. Abramovich, P. Wojtaszczyk, "On the uniqueness of order in the spaces $\text{I} _ { p }$ and $L _ { p } [ 0,1 ]$" ''Mat. Zametki'' , '''18''' (1975) pp. 313–325</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> C.D. Aliprantis, O. Burkinshaw, "Positive operators" , Acad. Press (1995)</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> D. Alspach, P. Enflo, E. Odell, "On the structure of separable $\mathcal{L} _ { p }$ spaces, $( 1 < p < \infty )$" ''Studia Math.'' , '''60''' (1977) pp. 79–90</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> C. Bennett, R. Sharpley, "Interpolation of operators" , Acad. Press (1988)</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> A.P. Calderón, "Intermediate spaces and interpolation, the complex method" ''Studia Math.'' , '''24''' (1964) pp. 113–190</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> P.G. Casazza, N.J. Kalton, D. Kutzarova, M. Mastylo, "Complex interpolation and complementably minimal spaces" N. Kalton (ed.) E. Saab (ed.) S. Montgomery-Smith (ed.) , ''Interaction between Functional Analysis, Harmonic Analysis, and Probability (Proc. Conf. Univ. Missouri 1994)'' , ''Lecture Notes Pure Appl. Math.'' , '''175''' , M. Dekker (1996) pp. 135–143</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> W.B. Johnson, B. Maurey, V. Schechtmannn, L. Tzafriri, "Symmetric structures in Banach spaces" ''Memoirs Amer. Math. Soc.'' , '''217''' (1979)</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> N.J. Kalton, "Lattice structures on Banach spaces" ''Memoirs Amer. Math. Soc.'' , '''493''' (1993)</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> N.J. Kalton, "The basic sequence problem" ''Studia Math.'' , '''116''' (1995) pp. 167–187</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> L.V. Kantorovich, G.P. Akilov, "Functional analysis" , Pergamon (1998)</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> S.G. Krein, Yu.I. Petunin, E.M. Semenov, "Interpolation of linear operators" , Amer. Math. Soc. (1982) (In Russian)</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> J. Lindenstrauss, L. Tzafriri, "Classical Banach spaces: Function spaces" , '''2''' , Springer (1979)</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> G.A. Lozanovskii, "On some Banach lattices" ''Sib. Math. J.'' , '''10''' (1969) pp. 419–430</td></tr><tr><td valign="top">[a14]</td> <td valign="top"> W.A.J. Luxemburg, A.C. Zaanen, "Riesz spaces" , '''2''' , North-Holland (1983)</td></tr><tr><td valign="top">[a15]</td> <td valign="top"> E. Odell, T. Schlumprecht, "The distortion problem" ''Acta Math.'' , '''173''' (1994) pp. 258–281</td></tr><tr><td valign="top">[a16]</td> <td valign="top"> G. Pisier, "Some applications of the complex interpolation method to Banach lattices" ''J. Anal. Math.'' , '''35''' (1979) pp. 264–281</td></tr></table> |
Latest revision as of 20:16, 25 January 2024
Let $( \Omega , \Sigma , \mu )$ be a complete $\sigma$-finite measure space and let $L ^ { 0 } ( \mu ) = L ^ { 0 } ( \Omega , \Sigma , \mu )$ be the space of all equivalence classes of $\mu$-measurable real-valued functions endowed with the topology of convergence in measure relative to each set of finite measure.
A Banach space $X \subset L ^ { 0 } ( \mu )$ is called a Banach function space on $( \Omega , \Sigma , \mu )$ if there exists a $u \in X$ such that $u > 0$ almost everywhere and $X$ satisfies the ideal property:
\begin{equation*} x \in L ^ { 0 } ( \mu ) , y \in X , | x | \leq | y | \mu - a.e. \end{equation*}
\begin{equation*} \Downarrow x \in X \text { and } \| x \| \leq \| y \|. \end{equation*}
The Lebesgue function spaces $L _ { p }$ ($1 \leq p \leq \infty$) play a primary role in many problems arising in mathematical analysis. There are other classes of Banach function spaces that are also of interest. The classes of Musielak–Orlicz, Lorentz and Marcinkiewicz spaces, for example, are of intrinsic importance (cf. also Orlicz space; Orlicz–Lorentz space; Marcinkiewicz space). Function spaces are important and natural examples of abstract Banach lattices (a Banach lattice is a Banach space that is also a vector lattice $X$ with the property that $\| x \| \leq \| y \|$ whenever $| x | \leq | y |$, where $| x | = x \vee ( - x )$, cf. also Banach lattice). A Banach lattice is said to be order continuous if $\| x _ { n } \| \rightarrow 0$ whenever $x _ { n } \downarrow 0$. The following very useful general representation result (see [a12]) allows one to reduce most of the proofs for a quite large class of abstract Banach lattices to the case of Banach function spaces: Let $X$ be an order-continuous Banach lattice with a weak unit (a weak unit is an element $e > 0$ such that $e \wedge | x | = 0$ implies $x = 0$). Then there exist a probability space $( \Omega , \Sigma , \mu )$ and a Banach function space $X$ on $( \Omega , \Sigma , \mu )$ such that $X$ is isometrically lattice-isomorphic to $X$ and $L _ { \infty } ( \mu ) \subset X \subset L _ { 1 } ( \mu )$ with continuous inclusions.
See [a2], [a7], [a10], [a14] for a general theory of Banach lattices.
A Banach function space $X$ is said to have the Fatou property if whenever $( f _ { n } )$ is a norm-bounded sequence in $X$ such that $0 \leq f _ { n } \uparrow f \in L ^ { 0 } ( \mu )$, then $f \in X$ and $\| f _ { n } \| \rightarrow \| f \|$.
In recent (1998) years a great deal of research went into the study of rearrangement-invariant function spaces, in particular of Orlicz spaces. General references to this area are e.g. [a7], [a11], [a12]. A Banach function space $X$ is said to be rearrangement invariant if whenever $f \in X$, $g \in L ^ { 0 } ( \mu )$, and $f$ and $g$ are equi-measurable, then $g \in X$ and $\| f \| = \| g \|$. Two functions $f$ and $g$ are called equi-measurable if $| f|$ and $| g |$ have identical distributions, that is,
\begin{equation*} \mu _ { f } ( \lambda ) = \mu \{ t \in \Omega : | f ( t ) | > \lambda \} = \mu _ { g } ( \lambda ) \end{equation*}
for all $\lambda > 0$.
In the study of rearrangement-invariant function spaces, the Boyd indices play an important role (see e.g. [a7], [a12], and Boyd index). The Boyd indices $p_{X} $ and $q_X$ of a rearrangement-invariant function space $X$ on $[0,1]$ or $[ 0 , \infty )$ are defined by
\begin{equation*} p _ { X } = \operatorname { lim } _ { s \rightarrow \infty } \frac { \operatorname { log } s } { \operatorname { log } \| D _ { s } \| _ { X } }, \end{equation*}
\begin{equation*} q _ { X } = \operatorname { lim } _ { s \rightarrow 0 + } \frac { \operatorname { log } s } { \operatorname { log } \| D _ { s } \| _ { X } }, \end{equation*}
where for $s > 0$, $D _ { S }$ denotes the dilation operator, defined by $D _ { s } f ( t ) = f ( t / s )$ for $f \in X$ (where $f$ is defined to be zero outside $[0,1]$ in the former case).
For example, consider the following results, which hold for every separable rearrangement-invariant function space $X$ on $[0,1]$:
i) $X$ has an unconditional basis if and only if $1 < p_{ X}$ and $q_{X} < \infty$ (see, e.g., [a11], [a12]);
ii) if $1 < p_{ X}$ and $q_{X} < \infty$, then $X$ is a primary, i.e., whenever $X = E \oplus F$, then at least one of $E$ and $F$ is isomorphic to $X$ (see [a3]).
Rearrangement-invariant function spaces play an important role in the theory of interpolation of operators (see [a4], [a11]). A remarkable result of A.P. Calderón [a5] on the characterization of all interpolation spaces between $L _ { 1 } = L _ { 1 } ( \mu )$ and $L _ { \infty } = L _ { \infty } ( \mu )$ asserts that $X$ is an interpolation space with respect to the couple $( L _ { 1 } , L _ { \infty } )$ (i.e., that every linear operator $T : L _ { 1 } + L _ { \infty } \rightarrow L _ { 1 } + L _ { \infty }$ such that $T : L _ { 1 } \rightarrow L _ { 1 }$ and $T : L _ { \infty } \rightarrow L _ { \infty }$ boundedly, also maps $X$ to $X$ boundedly) if and only if it has the following property: For every $g \in X$ and every $f \in L _ { 1 } + L _ { \infty }$, whenever $\int _ { 0 } ^ { t } f ^ { * } ( s ) d s \leq \int _ { 0 } ^ { t } g ^ { * } ( s ) d s$ for all $t > 0$, it follows that $f \in X$ and $\| f \|_X \leq C\| g \|_X$ for some absolute constant $C$.
Here, $f ^ { * }$ denotes the non-increasing rearrangement of $f$, which is defined by
\begin{equation*} f ^ { * } ( t ) = \operatorname { inf } \{ \lambda > 0 : \mu _ { f } ( \lambda ) \leq t \} \end{equation*}
for $t > 0$. In particular, Calderón's result implies that rearrangement-invariant function spaces which have the Fatou property or are separable are interpolation spaces between $L_1$ and $L _ { \infty }$.
The Köthe dual space $X ^ { \prime }$ of a Banach function space $X$ on $( \Omega , \Sigma , \mu )$ is defined to be the space of all $x ^ { \prime }$ for which $x x ^ { \prime } \in L _ { 1 } ( \mu )$ for each $x \in X$ (cf. also Köthe–Toeplitz dual). The space $X ^ { \prime }$ is a Banach function space endowed with the norm
\begin{equation*} \| x ^ { \prime } \| _ { X ^ { \prime } } = \operatorname { sup } \{ \int _ { \Omega } | x x ^ { \prime } | d \mu : \| x \| _ { X } \leq 1 \}. \end{equation*}
Moreover, $X ^ { \prime \prime } = X$ isometrically if and only if $X$ has the Fatou property.
It is important to describe the relation between the Köthe dual $X ^ { \prime }$ and the usual (topological) dual space $X ^ { * }$ of a Banach function space $X$. A linear functional $f$ on $X$ is said to be order continuous (or integral) if $f ( x _ { n } ) \rightarrow 0$ for every sequence $\{ x _ { n } \}$ in $X$ such that $x _ { n } \downarrow 0$ almost everywhere. Let $X ^ { * }_{c}$ be the space all order-continuous functionals. This is a closed and norm-one complemented subspace of $X ^ { * }$. Thus, $X ^ { * } = X _ { c } ^ { * } \oplus X _ { s } ^ { * }$, where $X _ { s } ^ { * }$ denotes a complement to $X ^ { * }_{c}$, called the space of all singular functionals on $X$. The space $X ^ { * }_{c}$ is always total on $X$ (cf. Total set). Furthermore, it is norming, i.e.,
\begin{equation*} \| x \| _ { X } = \operatorname { sup } \left\{ \left| \int _ { \Omega } x x ^ { \prime } d \mu \right| : x ^ { \prime } \in X ^ { \prime } , \| x ^ { \prime } \| _ { X ^ { \prime } } \leq 1 \right\}, \end{equation*}
if and only if the norm on $X$ is order semi-continuous, i.e., $\| f _ { n } \| \rightarrow \| f \|$ whenever $0 \leq f _ { n } \uparrow f \in X$. The mapping that assigns to every $x ^ { \prime } \in X ^ { \prime }$ the functional $x \mapsto \int _ { \Omega } x x ^ { \prime } d \mu$ on $X$ is an order-linear isometry from the Köthe dual space $X ^ { \prime }$ onto $X ^ { * }_{c}$. In this way $X ^ { * }_{c}$ is identified with $X ^ { \prime }$. In particular, if $X$ is an order-continuous Banach function space, then $X ^ { * }$ can be identified with $X ^ { \prime }$ (see [a10], [a12], [a14]).
There are many methods of constructing Banach function spaces which are intermediate in some sense between two given Banach function spaces. One such method is the following construction, again due to Calderón [a5]. See also [a13] for the generalized version due to G.A. Lozanovskii. Let $X _ { 0 }$ and $X _ { 1 }$ be two Banach function spaces on the same measure space $( \Omega , \Sigma , \mu )$. For each $\theta \in ( 0,1 )$, the lattice $X _ { \theta } = X _ { 0 } ^ { 1 - \theta } X _ { 1 } ^ { \theta }$ is defined to be the space of all $x \in L ^ { 0 } ( \mu )$ such that $| x | = | x _ { 0 } | ^ { 1 - \theta } | x _ { 1 } | ^ { \theta }$ $\mu$-almost everywhere for some $x _ { 0 } \in X _ { 0 }$ and $x _ { 1 } \in X _ { 1 }$. The space $X _ { \theta }$ is a Banach function space endowed with the norm
\begin{equation*} \| x \| _ { \theta } = \end{equation*}
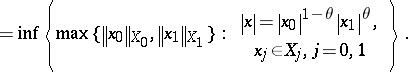 |
The identity $( X _ { 0 } ^ { 1 - \theta } X _ { 1 } ^ { \theta } ) ^ { \prime } = ( X _ { 0 } ^ { \prime } ) ^ { 1 - \theta } ( X _ { 1 } ^ { \prime } ) ^ { \theta }$ for all $0 < \theta < 1$ is an important result proved by Lozanovskii [a13]. Closely related results are the formula $X ^ { 1 / 2 } ( X ^ { \prime } ) ^ { 1 / 2 } = L _ { 2 }$, which holds for any Banach function space on $( \Omega , \Sigma , \mu )$, and also the Lozanovskii factorization theorem: For every $f \in L _ { 1 } ( \mu )$ and $\epsilon > 0$ there exist $x \in X$ and $y \in X ^ { \prime }$ such that $f = x y$ and $\|x \|_X \| y \| _ { X ^ { \prime } } \leq ( 1 + \epsilon ) \| f \| _ { L _ { 1 } }$. If $X$ has the Fatou property, the theorem is true for $\epsilon = 0$ as well.
This theorem has proved to be very useful in various applications (see, for example, [a9], [a15]).
Calderón's construction has found many other interesting applications in the study of Banach function spaces. An example is Pisier's theorem [a16], which says that if $1 < p < 2$, then a Banach function space on $( \Omega , \Sigma , \mu )$ is $p$-convex and $p ^ { \prime }$-concave if and only if $X = ( X _ { 0 } ) ^ { 1 - \theta } ( L _ { 2 } ( \mu ) ) ^ { \theta }$ for some Banach function space $X _ { 0 }$ on $( \Omega , \Sigma , \mu )$, with $\theta = 1 - 1 / p = 1 / p ^ { \prime }$. An application of this result and interpolation yields the following (see [a16]): Let $X$ be a $p$-convex and $p ^ { \prime }$-concave Banach function space for some $1 < p < 2$. Then every bounded linear operator from an $L_1$-space into $X$ is $( r , 1 )$-summing with $1 / r = 1 / p ^ { \prime } + 1 / 2$, i.e., if $( x _ { n } ) \subset L _ { 1 }$ is such that $\Sigma _ { n = 1 } ^ { \infty } | x ^ { * } ( x _ { n } ) | < \infty$ for all $x ^ { * } \in L _ { \infty }$, then $\Sigma _ { n = 1 } ^ { \infty } \| T _ { x _ { n } } \| _ { X } ^ { r } < \infty$ (cf. also Absolutely summing operator).
For another example see [a6], where the Calderón construction is used to construct a class of super-reflexive and complementably minimal Banach spaces (i.e., such that every infinite-dimensional closed subspace contains a complemented subspace isomorphic to a given space of this class) which are not isomorphic to $\text{I} _ { p }$ for any $p$.
One of the most interesting problems in the theory of Banach function spaces is to determine when two Banach function spaces which are isomorphic as Banach spaces are also lattice isomorphic. The first result of this type, due to Y.A. Abramovich and P. Wojtaszczyk [a1] says that $L_1$ has a unique structure as a non-atomic Banach function space (i.e., if $X$ is a non-atomic Banach function space isomorphic to $L_1$, then $X$ is lattice isomorphic to $L_1$). The general study of possible rearrangement-invariant lattice structures in Banach function spaces on $[0,1]$ or $[ 0 , \infty )$ was initiated in [a7], where, among other important results, it is shown that any rearrangement-invariant function space $X$ on $[0,1]$ which is isomorphic to $L _ { p } ( 0,1 )$, $1 \leq p \leq \infty$, is equal to $L _ { p } ( 0,1 )$ up to an equivalent renorming. See also [a8], where important general results on the uniqueness of the structure of Banach function spaces are presented.
References
| [a1] | Y.A. Abramovich, P. Wojtaszczyk, "On the uniqueness of order in the spaces $\text{I} _ { p }$ and $L _ { p } [ 0,1 ]$" Mat. Zametki , 18 (1975) pp. 313–325 |
| [a2] | C.D. Aliprantis, O. Burkinshaw, "Positive operators" , Acad. Press (1995) |
| [a3] | D. Alspach, P. Enflo, E. Odell, "On the structure of separable $\mathcal{L} _ { p }$ spaces, $( 1 < p < \infty )$" Studia Math. , 60 (1977) pp. 79–90 |
| [a4] | C. Bennett, R. Sharpley, "Interpolation of operators" , Acad. Press (1988) |
| [a5] | A.P. Calderón, "Intermediate spaces and interpolation, the complex method" Studia Math. , 24 (1964) pp. 113–190 |
| [a6] | P.G. Casazza, N.J. Kalton, D. Kutzarova, M. Mastylo, "Complex interpolation and complementably minimal spaces" N. Kalton (ed.) E. Saab (ed.) S. Montgomery-Smith (ed.) , Interaction between Functional Analysis, Harmonic Analysis, and Probability (Proc. Conf. Univ. Missouri 1994) , Lecture Notes Pure Appl. Math. , 175 , M. Dekker (1996) pp. 135–143 |
| [a7] | W.B. Johnson, B. Maurey, V. Schechtmannn, L. Tzafriri, "Symmetric structures in Banach spaces" Memoirs Amer. Math. Soc. , 217 (1979) |
| [a8] | N.J. Kalton, "Lattice structures on Banach spaces" Memoirs Amer. Math. Soc. , 493 (1993) |
| [a9] | N.J. Kalton, "The basic sequence problem" Studia Math. , 116 (1995) pp. 167–187 |
| [a10] | L.V. Kantorovich, G.P. Akilov, "Functional analysis" , Pergamon (1998) |
| [a11] | S.G. Krein, Yu.I. Petunin, E.M. Semenov, "Interpolation of linear operators" , Amer. Math. Soc. (1982) (In Russian) |
| [a12] | J. Lindenstrauss, L. Tzafriri, "Classical Banach spaces: Function spaces" , 2 , Springer (1979) |
| [a13] | G.A. Lozanovskii, "On some Banach lattices" Sib. Math. J. , 10 (1969) pp. 419–430 |
| [a14] | W.A.J. Luxemburg, A.C. Zaanen, "Riesz spaces" , 2 , North-Holland (1983) |
| [a15] | E. Odell, T. Schlumprecht, "The distortion problem" Acta Math. , 173 (1994) pp. 258–281 |
| [a16] | G. Pisier, "Some applications of the complex interpolation method to Banach lattices" J. Anal. Math. , 35 (1979) pp. 264–281 |
Banach function space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banach_function_space&oldid=16221