Balayage method
A method for solving the Dirichlet problem for the Laplace equation, developed by H. Poincaré ([1], [2], see also [4]), which will now be described. Let 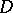 be a bounded domain of the Euclidean space
be a bounded domain of the Euclidean space 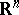 ,
, 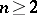 , let
, let 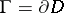 be the boundary of
be the boundary of 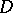 . Let
. Let 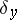 be the Dirac measure concentrated at the point
be the Dirac measure concentrated at the point 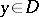 , let
, let 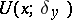 be the Newton potential of the measure
be the Newton potential of the measure 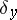 for
for 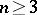 , or the logarithmic potential of the measure
, or the logarithmic potential of the measure 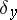 if
if 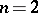 . A balayage (or sweeping) of the measure
. A balayage (or sweeping) of the measure 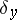 from the domain
from the domain 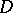 to the boundary
to the boundary 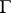 is a measure
is a measure  on
on 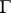 whose potential
whose potential 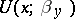 coincides outside
coincides outside 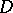 with
with 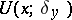 and is not larger than
and is not larger than 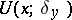 inside
inside 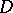 ; this measure
; this measure 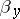 is unique and coincides with the harmonic measure on
is unique and coincides with the harmonic measure on 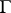 for the point
for the point 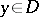 . The balayage of an arbitrary positive measure, concentrated on
. The balayage of an arbitrary positive measure, concentrated on 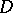 , is defined in a similar manner. If
, is defined in a similar manner. If 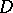 is a sphere, the density of the mass distribution
is a sphere, the density of the mass distribution 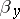 , i.e. the derivative of the measure
, i.e. the derivative of the measure 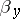 , is identical with the Poisson kernel (cf. Poisson integral). In general, if the boundary
, is identical with the Poisson kernel (cf. Poisson integral). In general, if the boundary 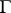 is sufficiently smooth, the measure
is sufficiently smooth, the measure 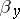 is absolutely continuous, and the density of the mass distribution
is absolutely continuous, and the density of the mass distribution 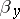 coincides with the normal derivative of the Green function for
coincides with the normal derivative of the Green function for 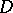 . The measure
. The measure 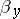 serves to write down the solution of the Dirichlet problem as the so-called formula of de la Vallée-Poussin:
serves to write down the solution of the Dirichlet problem as the so-called formula of de la Vallée-Poussin:
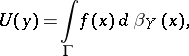 |
where 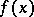 is a function defined on
is a function defined on 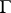 .
.
In his original publication on the balayage method, Poincaré began by demonstrating the geometrical construction of the process for a sphere. Then, basing himself on Harnack's theorems (cf. Harnack theorem) and on the fact that it is possible to exhaust the domain 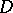 by a sequence of spheres
by a sequence of spheres 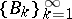 , he constructed an infinite sequence of potentials
, he constructed an infinite sequence of potentials 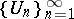 in which each potential
in which each potential 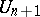 is obtained from the preceding one,
is obtained from the preceding one, 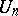 , by the balayage method of moving the masses from the domain
, by the balayage method of moving the masses from the domain 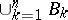 to its boundary, and which reduces to solving the Dirichlet problem for a sufficiently smooth domain
to its boundary, and which reduces to solving the Dirichlet problem for a sufficiently smooth domain 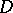 (for a detailed discussion of the conditions of applicability of the balayage method, see [3]).
(for a detailed discussion of the conditions of applicability of the balayage method, see [3]).
In modern potential theory [5], [6] the balayage problem is treated as an independent problem, resembling the Dirichlet problem, and it turns out that the balayaged measure can be considered on sets of a general nature. For instance, the balayage problem in its simplest form is to find, for a given mass distribution 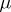 inside a closed domain
inside a closed domain 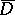 , a mass distribution
, a mass distribution  on
on 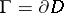 such that the potentials of both distributions coincide outside
such that the potentials of both distributions coincide outside 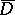 . If the boundary
. If the boundary 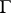 is smooth, the solution of the balayage problem for
is smooth, the solution of the balayage problem for 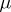 will be an absolutely continuous measure
will be an absolutely continuous measure  . Its density, or the derivative
. Its density, or the derivative 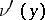 ,
, 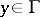 , may be written down in terms of the Green function
, may be written down in terms of the Green function 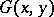 of the domain
of the domain 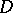 in the form
in the form
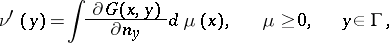 | (*) |
where 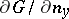 is the derivative of
is the derivative of 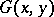 in the direction of the interior normal to
in the direction of the interior normal to 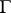 at the point
at the point 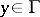 . Inside the domain
. Inside the domain 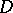 the potentials satisfy the inequality
the potentials satisfy the inequality 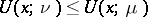 , i.e. balayage inside the domain results in a decrease of the potential. If
, i.e. balayage inside the domain results in a decrease of the potential. If 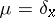 is the Dirac measure at the point
is the Dirac measure at the point 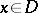 , formula (*) yields
, formula (*) yields 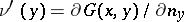 , i.e. the normal derivative of the Green function is the density of the measure obtained by balayage of the unit mass concentrated at the point
, i.e. the normal derivative of the Green function is the density of the measure obtained by balayage of the unit mass concentrated at the point 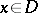 . Generalization of formula (*) yields an expression for the balayaged measure
. Generalization of formula (*) yields an expression for the balayaged measure 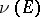 of an arbitrary Borel set
of an arbitrary Borel set 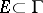 for an arbitrary domain
for an arbitrary domain 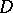 :
:
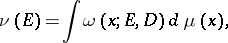 |
where 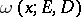 is the harmonic measure of
is the harmonic measure of 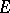 with respect to the domain
with respect to the domain 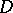 at the point
at the point  .
.
If 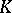 is an arbitrary compact set in
is an arbitrary compact set in 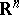 and
and 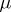 is a bounded positive Borel measure, the balayage (or sweeping) of the measure
is a bounded positive Borel measure, the balayage (or sweeping) of the measure 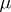 onto the compact set
onto the compact set 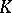 is a measure
is a measure  on
on 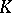 such that
such that 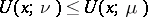 everywhere, and such that quasi-everywhere on
everywhere, and such that quasi-everywhere on 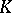 , i.e. with the possible exception of a set of points of exterior capacity zero,
, i.e. with the possible exception of a set of points of exterior capacity zero, 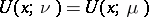 . Such a formulation of the balayage problem, which is more general than balayage from a domain, may also be extended to potentials of other types, e.g. Bessel potentials or Riesz potentials (cf. Bessel potential; Riesz potential). Balayage of measures onto arbitrary Borel sets
. Such a formulation of the balayage problem, which is more general than balayage from a domain, may also be extended to potentials of other types, e.g. Bessel potentials or Riesz potentials (cf. Bessel potential; Riesz potential). Balayage of measures onto arbitrary Borel sets 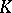 is also considered.
is also considered.
The problem of balayage for superharmonic functions (cf. Superharmonic function) has been similarly formulated. Let  be a non-negative superharmonic function on a domain
be a non-negative superharmonic function on a domain 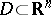 . The balayage of the function
. The balayage of the function  onto a compact set
onto a compact set 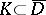 is the largest superharmonic function
is the largest superharmonic function 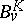 such that 1) its associated measure is concentrated on
such that 1) its associated measure is concentrated on 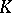 ; 2)
; 2) 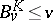 everywhere; and 3)
everywhere; and 3) 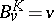 quasi-everywhere on
quasi-everywhere on 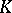 .
.
In abstract potential theory (cf. Potential theory, abstract) the balayage problem in both its formulations is solved for sets 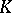 in an arbitrary harmonic space
in an arbitrary harmonic space 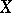 , i.e. in a locally compact topological space
, i.e. in a locally compact topological space 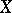 which permits the isolation of an axiomatically defined sheaf of harmonic functions. This axiomatic approach makes it possible to consider the balayage problem for potentials connected with partial differential equations of a more general nature [7]. For the balayage method in stochastics cf. [8].
which permits the isolation of an axiomatically defined sheaf of harmonic functions. This axiomatic approach makes it possible to consider the balayage problem for potentials connected with partial differential equations of a more general nature [7]. For the balayage method in stochastics cf. [8].
References
| [1] | H. Poincaré, "Sur les équations aux dérivees partielles de la physique mathématique" Amer. J. Math. , 12 : 3 (1890) pp. 211–294 |
| [2] | H. Poincaré, "Theorie du potentiel Newtonien" , Paris (1899) |
| [3] | Ch.J. de la Vallée-Poussin, "Le potentiel logarithmique, balayage et répresentation conforme" , Gauthier-Villars (1949) |
| [4] | L.N. Sretenskii, "Theory of the Newton potential" , Moscow-Leningrad (1946) (In Russian) |
| [5] | N.S. Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian) |
| [6] | M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1965) |
| [7] | C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972) |
| [8] | P.A. Meyer, "Probability and potentials" , Blaisdell (1966) |
Comments
Balayage is also referred to as sweeping of a measure. A classic reference for problems in potential theory related to Green functions is [a1].
In probabilistic potential theory the swept measure 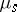 on
on 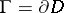 of a probability measure
of a probability measure 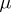 concentrated on
concentrated on 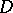 turns out to be the distribution of a standard Brownian motion on
turns out to be the distribution of a standard Brownian motion on  , which has initial distribution
, which has initial distribution 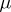 , at the moment of first hitting
, at the moment of first hitting 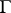 .
.
Another link with probabilistic potential theory is provided by the fact that, for each sufficiently nice harmonic space, there exists a Hunt process 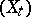 whose excessive functions are the positive hyper-harmonic functions. If
whose excessive functions are the positive hyper-harmonic functions. If 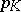 denotes the hitting distribution of a compact set
denotes the hitting distribution of a compact set 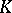 , then
, then 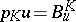 for positive superharmonic functions
for positive superharmonic functions  , and the balayage of a measure
, and the balayage of a measure  on
on 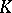 is given by
is given by 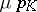 . Therefore, the notion of balayage of a function or a measure can also be defined in terms of the potential kernel of a semi-group of kernels, see [a3].
. Therefore, the notion of balayage of a function or a measure can also be defined in terms of the potential kernel of a semi-group of kernels, see [a3].
References
| [a1] | M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1975) |
| [a2] | J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984) pp. 390 |
| [a3] | C. Dellacherie, P.A. Meyer, "Probabilités et potentiel" , 1–2 , Hermann (1975–1983) |
Balayage method. E.D. Solomentsev (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Balayage_method&oldid=11819