Baer multiplication
From Encyclopedia of Mathematics
A binary operation on the set of classes of extensions of modules, proposed by R. Baer [1]. Let 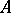 and
and 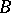 be arbitrary modules. An extension of
be arbitrary modules. An extension of 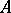 with kernel
with kernel 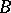 is an exact sequence:
is an exact sequence:
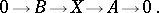 | (1) |
The extension (1) is called equivalent to the extension
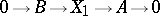 |
if there exists a homomorphism 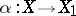 forming part of the commutative diagram
forming part of the commutative diagram
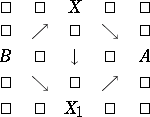 |
The set of equivalence classes of extensions is denoted by 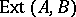 . The Baer multiplication on
. The Baer multiplication on 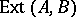 is induced by the operation of products of extensions defined as follows. Let
is induced by the operation of products of extensions defined as follows. Let
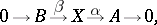 | (2) |
 | (3) |
be two extensions. In the direct sum  the submodules
the submodules
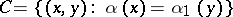 |
and
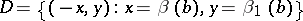 |
are selected. Clearly, 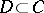 , so that one can define the quotient module
, so that one can define the quotient module 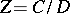 . The Baer product of the extensions (2) and (3) is the extension
. The Baer product of the extensions (2) and (3) is the extension
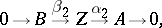 |
where
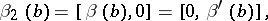 |
and
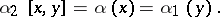 |
References
| [1] | R. Baer, "Erweiterung von Gruppen und ihren Isomorphismen" Math. Z. , 38 (1934) pp. 374–416 |
| [2] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) |
How to Cite This Entry:
Baer multiplication. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baer_multiplication&oldid=14712
Baer multiplication. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baer_multiplication&oldid=14712
This article was adapted from an original article by V.E. Govorov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article