Difference between revisions of "Attraction domain of a stable distribution"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
(refs format) |
||
| Line 35: | Line 35: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|GK}}|| B.V. Gnedenko, A.N. Kolmogorov, "Limit distributions for sums of independent random variables" , Addison-Wesley (1954) (Translated from Russian) {{MR|0062975}} {{ZBL|0056.36001}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|IL}}|| I.A. Ibragimov, Yu.V. Linnik, "Independent and stationary sequences of random variables" , Wolters-Noordhoff (1971) (Translated from Russian) {{MR|0322926}} {{ZBL|0219.60027}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|P}}|| V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian) {{MR|0388499}} {{ZBL|0322.60043}} {{ZBL|0322.60042}} | ||
| + | |} | ||
Revision as of 19:55, 10 May 2012
domain of attraction of a stable distribution
2020 Mathematics Subject Classification: Primary: 60F05 Secondary: 60E07 [MSN][ZBL]
The totality of all distribution functions 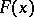 such that for a sequence of independent identically-distributed random variables
such that for a sequence of independent identically-distributed random variables 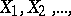 with distribution function
with distribution function  and for a suitable choice of constants
and for a suitable choice of constants 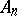 and
and 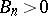 ,
, 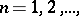 the distribution of the random variable
the distribution of the random variable
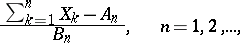 | (*) |
converges weakly, as 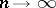 , to a non-degenerate distribution function
, to a non-degenerate distribution function 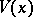 , which is necessarily stable.
, which is necessarily stable.
One of the fundamental problems in the theory of stable laws is the description of domains of attraction of stable laws. Thus, for the normal distribution, A.Ya. Khinchin, W. Feller and P. Lévy established in 1935 that 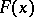 belongs to the domain of attraction of a normal law if and only if, as
belongs to the domain of attraction of a normal law if and only if, as 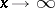 ,
,
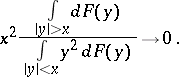 |
Later B.V. Gnedenko and W. Doeblin (1940) gave a description of the domain of attraction of a stable law with exponent 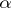 ,
, 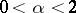 :
: 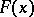 belongs to the domain of attraction of a non-degenerate stable law
belongs to the domain of attraction of a non-degenerate stable law 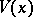 with exponent
with exponent 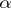 if and only if:
if and only if:
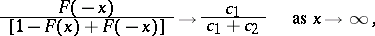 |
for some 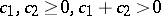 , determined by
, determined by  , and
, and
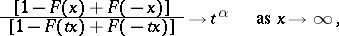 |
for each constant 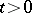 . Restriction on the behaviour of the normalizing coefficients
. Restriction on the behaviour of the normalizing coefficients  ,
,  leads to narrower classes of distribution functions for which the convergence in distribution (*) holds. The set of distribution functions
leads to narrower classes of distribution functions for which the convergence in distribution (*) holds. The set of distribution functions 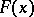 for which (*) converges weakly, for a suitable choice of
for which (*) converges weakly, for a suitable choice of 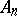 ,
, 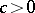 and
and 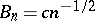 ,
, 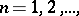 to a stable distribution function
to a stable distribution function 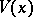 with exponent
with exponent 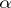 , is called the normal domain of attraction for
, is called the normal domain of attraction for 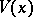 . The normal domain of attraction of a normal distribution coincides with the set of non-degenerate distributions with a finite variance.
. The normal domain of attraction of a normal distribution coincides with the set of non-degenerate distributions with a finite variance.
The normal domain of attraction of a non-degenerate stable distribution function 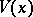 with exponent
with exponent 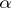 (
(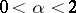 ) is formed by the functions
) is formed by the functions 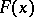 for which
for which
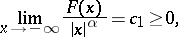 |
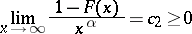 |
exist and are finite, where 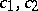 are determined by
are determined by 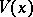 .
.
References
| [GK] | B.V. Gnedenko, A.N. Kolmogorov, "Limit distributions for sums of independent random variables" , Addison-Wesley (1954) (Translated from Russian) MR0062975 Zbl 0056.36001 |
| [IL] | I.A. Ibragimov, Yu.V. Linnik, "Independent and stationary sequences of random variables" , Wolters-Noordhoff (1971) (Translated from Russian) MR0322926 Zbl 0219.60027 |
| [P] | V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian) MR0388499 Zbl 0322.60043 Zbl 0322.60042 |
Attraction domain of a stable distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Attraction_domain_of_a_stable_distribution&oldid=23577