Difference between revisions of "Association scheme"
m (link) |
(TeX partly done) |
||
| Line 3: | Line 3: | ||
Association schemes provide the appropriate setting for treating certain problems from several different areas of algebraic combinatorics, for example, coding theory, design theory, algebraic graph theory, finite group theory, and finite geometry. The following definition is equivalent to that of Delsarte (1973). | Association schemes provide the appropriate setting for treating certain problems from several different areas of algebraic combinatorics, for example, coding theory, design theory, algebraic graph theory, finite group theory, and finite geometry. The following definition is equivalent to that of Delsarte (1973). | ||
| − | An association scheme | + | An association scheme $\mathcal{A}$ with $d$ classes is a finite set $X$ together with $d+1$ relations $R_i$ on $X$ such that: |
| − | i) | + | i) $\{R_0,\ldots,R_d\}$ is a partition of $X \times X$; |
| − | ii) | + | ii) $R_0 = \{(x,x) : x \in X\}$; |
| − | iii) For each | + | iii) For each $R_i$ in $\mathcal{A}$ there is a unique $R_j$ in $\mathcal{A}$ for which $(x,y) \in R_i$ if and only if $(y,x) \in R_j$; that is, $R_j = R_i^\top$; |
| − | iv) for any | + | iv) for any $(x,y) \in R_k$, the number $p_{ij}^k$ of $z$ with $(x,z) \in R_i$ and $(z,y) \in R_j$ depends only on $i,j,k$; |
| − | v) | + | v) $p_{ij}^k = p_{ji}^k$ for all $i,j,k \in \{0,\ldots,d\}$. |
The numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120300/a12030025.png" /> are called the intersection numbers of the association scheme. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120300/a12030026.png" />, put <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120300/a12030027.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120300/a12030028.png" />. Note that for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120300/a12030029.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120300/a12030030.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120300/a12030031.png" /> is a simple [[Graph|graph]] which is regular of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120300/a12030032.png" />. Indeed, a pair of complementary strongly regular graphs is equivalent to an association scheme with two classes. | The numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120300/a12030025.png" /> are called the intersection numbers of the association scheme. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120300/a12030026.png" />, put <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120300/a12030027.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120300/a12030028.png" />. Note that for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120300/a12030029.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120300/a12030030.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120300/a12030031.png" /> is a simple [[Graph|graph]] which is regular of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120300/a12030032.png" />. Indeed, a pair of complementary strongly regular graphs is equivalent to an association scheme with two classes. | ||
| Line 54: | Line 54: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Bannai, T. Ito, "Algebraic combinatorics I: association schemes" , ''Lecture Notes'' , '''58''' , Benjamin-Cummings (1984)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N.L. Biggs, "Algebraic graph theory" , ''Tracts in Math.'' , '''67''' , Cambridge Univ. Press (1974)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R.C. Bose, D.M. Mesner, "On linear associative algebras corresponding to association schemes of partially balanced designs" ''Ann. Math. Stat.'' , '''30''' (1959) pp. 21–38</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> R.C. Bose, T. Shimamoto, "Classification and analysis of partially balanced incomplete block designs with two associate classes" ''J. Amer. Statist. Assoc.'' , '''47''' (1952) pp. 151–184</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> A.E. Brouwer, "Strongly regular graphs" C.J. Colbourn (ed.) J.H. Dinitz (ed.) , ''The CRC Handbook of Combinatorial Designs'' , CRC (1996) pp. Part VI, Chapt. 5</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> A.E. Brouwer, A.M. Cohen, A. Neumaier, "Distance-regular graphs" , ''Ergebn. Math. (3)'' , '''18''' , Springer (1989)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> P.J. Cameron, J.H. van Lint, "Designs, graphs, codes and their links" , ''London Math. Soc. Student Texts'' , '''22''' , Cambridge Univ. Press (1991)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> Ph. Delsarte, "An algebraic approach to the association schemes of coding theory" ''Philips Research Reports Suppl.'' , '''10''' (1973)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> C.D. Godsil, "Algebraic combinatorics" , Chapman&Hall (1993)</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> D.G. Higman, "Invariant relations, coherent configurations and generalized polygons" M. Hall Jr. (ed.) J.H. van Lint (ed.) , ''Combinatorics'' , ''Math. Centre Tracts'' , '''57''' , Reidel (1975) pp. 347–363</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> D.G. Higman, "Coherent configurations, Part I: Ordinary representation theory" ''Geom. Dedicata'' , '''4''' (1975) pp. 1–32</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> D.G. Higman, "Coherent configurations, Part II: Weights" ''Geom. Dedicata'' , '''5''' (1976) pp. 413–424</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> S. Hobart, S.E. Payne, "Reconstructing a generalized quadrangle from its distance two association scheme" ''J. Algebraic Combin.'' , '''2''' (1993) pp. 261–266</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> F.J. MacWilliams, N.J.A. Sloane, "The theory of error–correcting codes" , North-Holland (1977)</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> S.E. Payne, J.A. Thas, "Finite generalized quadrangles" , Pitman (1984)</TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> P. Terwilliger, "The subconstituent algebra of an association scheme (part III)" ''J. Algebraic Combin.'' , '''2''' (1993) pp. 177–103</TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> P. Terwilliger, "Algebraic graph theory" ''Notes, January'' (1994)</TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> H. Wielandt, "Finite permutation groups" , Acad. Press (1964)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Bannai, T. Ito, "Algebraic combinatorics I: association schemes" , ''Lecture Notes'' , '''58''' , Benjamin-Cummings (1984)</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> N.L. Biggs, "Algebraic graph theory" , ''Tracts in Math.'' , '''67''' , Cambridge Univ. Press (1974)</TD></TR> | ||
| + | <TR><TD valign="top">[a3]</TD> <TD valign="top"> R.C. Bose, D.M. Mesner, "On linear associative algebras corresponding to association schemes of partially balanced designs" ''Ann. Math. Stat.'' , '''30''' (1959) pp. 21–38</TD></TR> | ||
| + | <TR><TD valign="top">[a4]</TD> <TD valign="top"> R.C. Bose, T. Shimamoto, "Classification and analysis of partially balanced incomplete block designs with two associate classes" ''J. Amer. Statist. Assoc.'' , '''47''' (1952) pp. 151–184</TD></TR> | ||
| + | <TR><TD valign="top">[a5]</TD> <TD valign="top"> A.E. Brouwer, "Strongly regular graphs" C.J. Colbourn (ed.) J.H. Dinitz (ed.) , ''The CRC Handbook of Combinatorial Designs'' , CRC (1996) pp. Part VI, Chapt. 5</TD></TR> | ||
| + | <TR><TD valign="top">[a6]</TD> <TD valign="top"> A.E. Brouwer, A.M. Cohen, A. Neumaier, "Distance-regular graphs" , ''Ergebn. Math. (3)'' , '''18''' , Springer (1989)</TD></TR> | ||
| + | <TR><TD valign="top">[a7]</TD> <TD valign="top"> P.J. Cameron, J.H. van Lint, "Designs, graphs, codes and their links" , ''London Math. Soc. Student Texts'' , '''22''' , Cambridge Univ. Press (1991)</TD></TR> | ||
| + | <TR><TD valign="top">[a8]</TD> <TD valign="top"> Ph. Delsarte, "An algebraic approach to the association schemes of coding theory" ''Philips Research Reports Suppl.'' , '''10''' (1973)</TD></TR> | ||
| + | <TR><TD valign="top">[a9]</TD> <TD valign="top"> C.D. Godsil, "Algebraic combinatorics" , Chapman&Hall (1993)</TD></TR> | ||
| + | <TR><TD valign="top">[a10]</TD> <TD valign="top"> D.G. Higman, "Invariant relations, coherent configurations and generalized polygons" M. Hall Jr. (ed.) J.H. van Lint (ed.) , ''Combinatorics'' , ''Math. Centre Tracts'' , '''57''' , Reidel (1975) pp. 347–363</TD></TR> | ||
| + | <TR><TD valign="top">[a11]</TD> <TD valign="top"> D.G. Higman, "Coherent configurations, Part I: Ordinary representation theory" ''Geom. Dedicata'' , '''4''' (1975) pp. 1–32</TD></TR> | ||
| + | <TR><TD valign="top">[a12]</TD> <TD valign="top"> D.G. Higman, "Coherent configurations, Part II: Weights" ''Geom. Dedicata'' , '''5''' (1976) pp. 413–424</TD></TR> | ||
| + | <TR><TD valign="top">[a13]</TD> <TD valign="top"> S. Hobart, S.E. Payne, "Reconstructing a generalized quadrangle from its distance two association scheme" ''J. Algebraic Combin.'' , '''2''' (1993) pp. 261–266</TD></TR> | ||
| + | <TR><TD valign="top">[a14]</TD> <TD valign="top"> F.J. MacWilliams, N.J.A. Sloane, "The theory of error–correcting codes" , North-Holland (1977)</TD></TR> | ||
| + | <TR><TD valign="top">[a15]</TD> <TD valign="top"> S.E. Payne, J.A. Thas, "Finite generalized quadrangles" , Pitman (1984)</TD></TR> | ||
| + | <TR><TD valign="top">[a16]</TD> <TD valign="top"> P. Terwilliger, "The subconstituent algebra of an association scheme (part III)" ''J. Algebraic Combin.'' , '''2''' (1993) pp. 177–103</TD></TR> | ||
| + | <TR><TD valign="top">[a17]</TD> <TD valign="top"> P. Terwilliger, "Algebraic graph theory" ''Notes, January'' (1994)</TD></TR> | ||
| + | <TR><TD valign="top">[a18]</TD> <TD valign="top"> H. Wielandt, "Finite permutation groups" , Acad. Press (1964)</TD></TR> | ||
| + | </table> | ||
| + | |||
| + | {{TEX|part}} | ||
Revision as of 18:13, 9 February 2018
Association schemes were introduced by R.C. Bose and T. Shimamoto [a4], studied further via the Bose–Mesner algebra introduced in [a3], generalized and given a most important impetus by P. Delsarte [a8], and generalized further by D.G. Higman [a10], [a11], [a12] to the theory of coherent configurations. The first text devoted to the theory is [a1]. A recent text that develops the theory both quite generally and quite extensively is [a9].
Association schemes provide the appropriate setting for treating certain problems from several different areas of algebraic combinatorics, for example, coding theory, design theory, algebraic graph theory, finite group theory, and finite geometry. The following definition is equivalent to that of Delsarte (1973).
An association scheme $\mathcal{A}$ with $d$ classes is a finite set $X$ together with $d+1$ relations $R_i$ on $X$ such that:
i) $\{R_0,\ldots,R_d\}$ is a partition of $X \times X$;
ii) $R_0 = \{(x,x) : x \in X\}$;
iii) For each $R_i$ in $\mathcal{A}$ there is a unique $R_j$ in $\mathcal{A}$ for which $(x,y) \in R_i$ if and only if $(y,x) \in R_j$; that is, $R_j = R_i^\top$;
iv) for any $(x,y) \in R_k$, the number $p_{ij}^k$ of $z$ with $(x,z) \in R_i$ and $(z,y) \in R_j$ depends only on $i,j,k$;
v) $p_{ij}^k = p_{ji}^k$ for all $i,j,k \in \{0,\ldots,d\}$.
The numbers 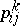 are called the intersection numbers of the association scheme. For
are called the intersection numbers of the association scheme. For 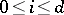 , put
, put 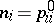 , and
, and 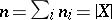 . Note that for each
. Note that for each 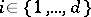 for which
for which 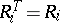 ,
, 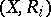 is a simple graph which is regular of degree
is a simple graph which is regular of degree 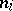 . Indeed, a pair of complementary strongly regular graphs is equivalent to an association scheme with two classes.
. Indeed, a pair of complementary strongly regular graphs is equivalent to an association scheme with two classes.
The Bose–Mesner algebra is the matrix algebra generated by the 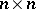 adjacency matrices
adjacency matrices 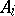 of
of 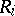 , where
, where
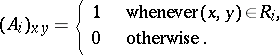 |
The matrices 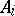 sum to
sum to  (the matrix whose every entry is
(the matrix whose every entry is 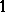 ),
), 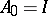 , and
, and 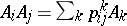 , for all
, for all 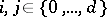 . The matrices
. The matrices 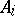 are linearly independent and generate a commutative
are linearly independent and generate a commutative 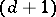 -dimensional semi-simple algebra
-dimensional semi-simple algebra 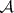 with a unique basis of minimal idempotents
with a unique basis of minimal idempotents 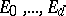 . The interplay between the two bases for
. The interplay between the two bases for 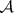 leads to useful restrictions on the various parameters, for example the so-called Krein conditions (discovered by L.L. Scott Jr., 1973). These restrictions are given as follows: Write
leads to useful restrictions on the various parameters, for example the so-called Krein conditions (discovered by L.L. Scott Jr., 1973). These restrictions are given as follows: Write
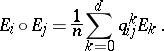 |
Then the Krein parameters 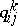 are all non-negative.
are all non-negative.
The matrix 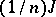 is a minimal idempotent, and one may take
is a minimal idempotent, and one may take 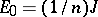 . Let
. Let 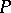 and
and 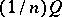 be the matrices relating the two bases for
be the matrices relating the two bases for 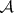 :
:
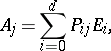 |
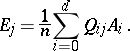 |
It follows that 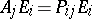 , which implies that the
, which implies that the 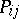 are eigenvalues of
are eigenvalues of 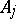 , and the columns of
, and the columns of 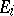 are the corresponding eigenvectors. Thus,
are the corresponding eigenvectors. Thus, 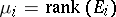 is the multiplicity of the eigenvalue
is the multiplicity of the eigenvalue 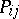 of
of 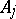 . The fact that the
. The fact that the 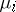 must all be integers is known as the rationality condition for an association scheme.
must all be integers is known as the rationality condition for an association scheme.
Delsarte's linear programming bound.
Let 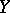 be a non-empty subset of the underlying set
be a non-empty subset of the underlying set 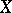 for a symmetric association scheme. Define the inner distribution
for a symmetric association scheme. Define the inner distribution  of
of 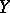 by
by
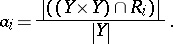 |
So, 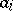 is the average number of points in
is the average number of points in  in relation
in relation 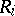 with a fixed point of
with a fixed point of 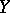 . Then Delsarte's linear programming bound says that
. Then Delsarte's linear programming bound says that 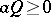 . This set of inequalities has been used to obtain upper bounds on the size of cliques and lower bounds on the size of designs in various structures.
. This set of inequalities has been used to obtain upper bounds on the size of cliques and lower bounds on the size of designs in various structures.
Examples.
Two of the most studied association schemes are the Johnson and Hamming schemes. The Johnson scheme 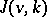 has for its set
has for its set 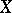 the set of all
the set of all 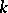 -subsets of a set of size
-subsets of a set of size  . Then
. Then 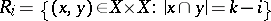 . The Hamming scheme
. The Hamming scheme 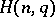 has the set of all words of length
has the set of all words of length  over an alphabet of
over an alphabet of 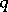 symbols as its set
symbols as its set 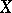 . The relation
. The relation 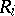 consists of all pairs
consists of all pairs 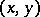 for which the Hamming distance (cf. also Error-correcting code) between
for which the Hamming distance (cf. also Error-correcting code) between  and
and 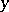 is
is  .
.
The finite generalized  -gons with parameters
-gons with parameters 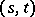 introduced by J. Tits (see [a15]) provide examples of strongly regular graphs to which the theory of association schemes may be applied. The rationality conditions can be used to show that
introduced by J. Tits (see [a15]) provide examples of strongly regular graphs to which the theory of association schemes may be applied. The rationality conditions can be used to show that 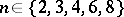 . The Krein conditions force
. The Krein conditions force 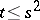 for
for 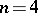 or
or 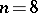 , and
, and 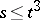 for
for 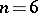 . For a different type of application of the theory of association schemes to finite generalized
. For a different type of application of the theory of association schemes to finite generalized 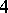 -gons (i.e., generalized quadrangles, cf. also Quadrangle; Quadrangle, complete), see [a13].
-gons (i.e., generalized quadrangles, cf. also Quadrangle; Quadrangle, complete), see [a13].
An association scheme with just two classes is equivalent to a pair of complementary strongly regular graphs. The theory of strongly regular graphs is subsumed in the theory of distance-regular graphs. Start with a connected simple graph 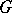 with vertex set
with vertex set 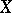 of diameter
of diameter 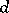 . Define
. Define 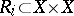 by
by 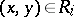 whenever
whenever  and
and 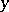 are at distance
are at distance 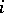 in
in 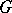 . When this defines an association scheme, the graph
. When this defines an association scheme, the graph 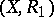 is called distance-regular. Many of the association schemes that arise in combinatorics are of this type. The major reference for distance-regular graphs is [a6]. A more modest introduction to the subject is [a2]. See [a5] for a table of strongly regular graphs with at most
is called distance-regular. Many of the association schemes that arise in combinatorics are of this type. The major reference for distance-regular graphs is [a6]. A more modest introduction to the subject is [a2]. See [a5] for a table of strongly regular graphs with at most  vertices. For many applications to coding theory see [a8], [a14], [a7].
vertices. For many applications to coding theory see [a8], [a14], [a7].
Let 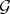 be a permutation group acting on a set
be a permutation group acting on a set 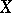 . Then
. Then 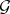 has a natural action on
has a natural action on  whose orbits are known as orbitals. If for each pair
whose orbits are known as orbitals. If for each pair 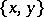 of distinct elements of
of distinct elements of 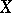 there is an element of
there is an element of 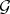 interchanging
interchanging  and
and  , then the orbitals form an association scheme. The Bose–Mesner algebra in this case is known as the centralizer algebra, and the standard results (as given in [a18], for example) have their analogues for the Bose–Mesner algebra. With no special hypotheses on the permutation group
, then the orbitals form an association scheme. The Bose–Mesner algebra in this case is known as the centralizer algebra, and the standard results (as given in [a18], for example) have their analogues for the Bose–Mesner algebra. With no special hypotheses on the permutation group  a coherent configuration is obtained, a natural motivation for the work of Higman [a10], [a11], [a12].
a coherent configuration is obtained, a natural motivation for the work of Higman [a10], [a11], [a12].
P. Terwilliger (see [a16] and its references) has pushed the theory of association schemes much further, and in [a17] has extended the Bose–Mesner algebra to what is now sometimes called the Terwilliger algebra.
References
| [a1] | E. Bannai, T. Ito, "Algebraic combinatorics I: association schemes" , Lecture Notes , 58 , Benjamin-Cummings (1984) |
| [a2] | N.L. Biggs, "Algebraic graph theory" , Tracts in Math. , 67 , Cambridge Univ. Press (1974) |
| [a3] | R.C. Bose, D.M. Mesner, "On linear associative algebras corresponding to association schemes of partially balanced designs" Ann. Math. Stat. , 30 (1959) pp. 21–38 |
| [a4] | R.C. Bose, T. Shimamoto, "Classification and analysis of partially balanced incomplete block designs with two associate classes" J. Amer. Statist. Assoc. , 47 (1952) pp. 151–184 |
| [a5] | A.E. Brouwer, "Strongly regular graphs" C.J. Colbourn (ed.) J.H. Dinitz (ed.) , The CRC Handbook of Combinatorial Designs , CRC (1996) pp. Part VI, Chapt. 5 |
| [a6] | A.E. Brouwer, A.M. Cohen, A. Neumaier, "Distance-regular graphs" , Ergebn. Math. (3) , 18 , Springer (1989) |
| [a7] | P.J. Cameron, J.H. van Lint, "Designs, graphs, codes and their links" , London Math. Soc. Student Texts , 22 , Cambridge Univ. Press (1991) |
| [a8] | Ph. Delsarte, "An algebraic approach to the association schemes of coding theory" Philips Research Reports Suppl. , 10 (1973) |
| [a9] | C.D. Godsil, "Algebraic combinatorics" , Chapman&Hall (1993) |
| [a10] | D.G. Higman, "Invariant relations, coherent configurations and generalized polygons" M. Hall Jr. (ed.) J.H. van Lint (ed.) , Combinatorics , Math. Centre Tracts , 57 , Reidel (1975) pp. 347–363 |
| [a11] | D.G. Higman, "Coherent configurations, Part I: Ordinary representation theory" Geom. Dedicata , 4 (1975) pp. 1–32 |
| [a12] | D.G. Higman, "Coherent configurations, Part II: Weights" Geom. Dedicata , 5 (1976) pp. 413–424 |
| [a13] | S. Hobart, S.E. Payne, "Reconstructing a generalized quadrangle from its distance two association scheme" J. Algebraic Combin. , 2 (1993) pp. 261–266 |
| [a14] | F.J. MacWilliams, N.J.A. Sloane, "The theory of error–correcting codes" , North-Holland (1977) |
| [a15] | S.E. Payne, J.A. Thas, "Finite generalized quadrangles" , Pitman (1984) |
| [a16] | P. Terwilliger, "The subconstituent algebra of an association scheme (part III)" J. Algebraic Combin. , 2 (1993) pp. 177–103 |
| [a17] | P. Terwilliger, "Algebraic graph theory" Notes, January (1994) |
| [a18] | H. Wielandt, "Finite permutation groups" , Acad. Press (1964) |
Association scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Association_scheme&oldid=42808