Artin-Schreier code
Given an algebraic curve  , where
, where  is a field of characteristic
is a field of characteristic  , a covering
, a covering  is called an Artin–Schreier curve over
is called an Artin–Schreier curve over  if the corresponding extension of function fields
if the corresponding extension of function fields  is generated by some function
is generated by some function  such that
such that  (where
(where 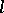 is a power of
is a power of 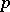 , cf. also Extension of a field). If
, cf. also Extension of a field). If  is a finite field, it turns out that Artin–Schreier curves often have many rational points.
is a finite field, it turns out that Artin–Schreier curves often have many rational points.
To be precise, let 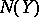 (respectively,
(respectively, 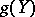 ) denote the number of
) denote the number of 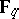 -rational points (respectively, the genus) of a curve
-rational points (respectively, the genus) of a curve 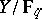 . The Hasse–Weil theorem states that
. The Hasse–Weil theorem states that
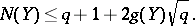 |
If the genus is large with respect to 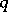 , this bound can be improved as follows. Let
, this bound can be improved as follows. Let 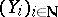 be a sequence of curves over
be a sequence of curves over 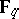 such that
such that 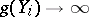 . Then
. Then
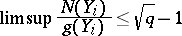 |
(the Drinfel'd–Vladut bound).
Curves over 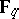 can be used to construct error-correcting linear codes, so-called geometric Goppa codes or algebraic-geometric codes (cf. Error-correcting code; Goppa code; Algebraic-geometric code; [a4], [a5]). If the curves have sufficiently may rational points, these codes have very good error-correcting properties. Hence, one is interested in explicit constructions of curves with many rational points.
can be used to construct error-correcting linear codes, so-called geometric Goppa codes or algebraic-geometric codes (cf. Error-correcting code; Goppa code; Algebraic-geometric code; [a4], [a5]). If the curves have sufficiently may rational points, these codes have very good error-correcting properties. Hence, one is interested in explicit constructions of curves with many rational points.
Examples of Artin–Schreier curves.
The Hermitian curve over 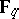 , for
, for 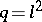 , is given by the equation
, is given by the equation 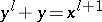 . It has
. It has 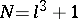 rational points and its genus is
rational points and its genus is 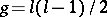 . Hence, for it the Hasse–Weil bound
. Hence, for it the Hasse–Weil bound 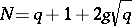 is attained, see [a4].
is attained, see [a4].
Again, let 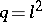 be a square. Define a tower of function fields
be a square. Define a tower of function fields 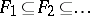 over
over 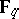 (cf. Tower of fields) by
(cf. Tower of fields) by 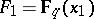 ,
, 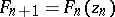 , where
, where
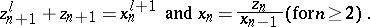 |
For the corresponding algebraic curves 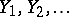 , the coverings
, the coverings 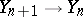 are Artin–Schreier curves. This sequence
are Artin–Schreier curves. This sequence 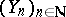 attains the Drinfel'd–Vladut bound, i.e.,
attains the Drinfel'd–Vladut bound, i.e., 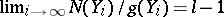 (see [a1]).
(see [a1]).
The geometric Goppa codes constructed using these curves 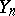 beat the Gilbert–Varshamov bound (cf. also Error-correcting code; [a3]) for all
beat the Gilbert–Varshamov bound (cf. also Error-correcting code; [a3]) for all 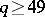 . This construction is simpler and more explicit than the construction based on modular curves (the Tsfasman–Vladut–Zink theorem, [a5]).
. This construction is simpler and more explicit than the construction based on modular curves (the Tsfasman–Vladut–Zink theorem, [a5]).
References
| [a1] | A. Garcia, H. Stichtenoth, "A tower of Artin–Schreier extensions of function fields attaining the Drinfeld–Vladut bound" Invent. Math. , 121 (1995) pp. 211–222 |
| [a2] | G. van der Geer, M. van der Vlugt, "Curves over finite fields of characteristic two with many rational points" C.R. Acad. Sci. Paris , 317 (1993) pp. 693–697 |
| [a3] | J.H. van Lint, "Introduction to coding theory" , Springer (1992) |
| [a4] | H. Stichtenoth, "Algebraic function fields and codes" , Springer (1993) ISBN 3-540-58469-6 Zbl 0816.14011 |
| [a5] | M.A. Tsfasman, S.G. Vladut, "Algebraic geometric codes" , Kluwer Acad. Publ. (1991) |
Artin-Schreier code. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Artin-Schreier_code&oldid=42797