Difference between revisions of "Arbitration scheme"
m (→Comments: link) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | a0130501.png | ||
| + | $#A+1 = 41 n = 3 | ||
| + | $#C+1 = 41 : ~/encyclopedia/old_files/data/A013/A.0103050 Arbitration scheme | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A rule by which each arbitration game (cf. [[Cooperative game|Cooperative game]]) is put into correspondence with a unique outcome of the game is called an arbitration solution. The first arbitration scheme was considered by J. Nash [[#References|[1]]] for the case of a two-person game. Let $ R= \{ u = ( u _ {1} \dots u _ {n} ) \} $ | |
| + | be the set of outcomes, let $ d = ( d _ {1} \dots d _ {n} ) $ | ||
| + | be the status quo point, i.e. the point corresponding to the situation in which no cooperative outcome is realized, let $ [ R, d ] $ | ||
| + | be the corresponding arbitration game and let $ \overline{u}\; $ | ||
| + | be an arbitration solution of it. An outcome $ u ^ {*} $ | ||
| + | is called a Nash solution if | ||
| − | + | $$ | |
| + | \prod _ { i } ( u _ {i} ^ {*} - d _ {i} ) = \max _ | ||
| + | {u \in R } \prod _ { i } ( u _ {i} - d _ {i} ) . | ||
| + | $$ | ||
| − | + | Only a Nash solution satisfies the following axioms: 1) if $ f $ | |
| + | is a linear non-decreasing mapping then $ f \overline{u}\; $ | ||
| + | is an arbitration solution of the game $ [ fR, fd ] $( | ||
| + | invariance with respect to utility transformations); 2) $ \overline{u}\; \geq d $, | ||
| + | $ \overline{u}\; \in R $ | ||
| + | and there is no $ u \in R $ | ||
| + | such that $ u \geq \overline{u}\; $( | ||
| + | Pareto optimality); 3) if $ R ^ \prime \subset R $, | ||
| + | $ d ^ \prime = d $, | ||
| + | $ \overline{u}\; \in R ^ \prime $, | ||
| + | then $ \overline{u}\; {} ^ \prime = \overline{u}\; $( | ||
| + | independence of irrelevant alternatives); and 4) if $ d _ {i} = d _ {j} $, | ||
| + | $ i, j = 1 \dots n $, | ||
| + | and $ R $ | ||
| + | is symmetric, then $ \overline{u}\; _ {i} = \overline{u}\; _ {j} $, | ||
| + | $ i, j = 1 \dots n $( | ||
| + | symmetry). | ||
| − | + | Another arbitration scheme for an $ n $- | |
| + | person game with characteristic function $ v $ | ||
| + | and player set $ N = \{ 1 \dots n \} $ | ||
| + | was given by L.S. Shapley [[#References|[2]]]. The Shapley solution $ \phi (v) = ( \phi _ {1} (v) \dots \phi _ {n} (v) ) $, | ||
| + | where | ||
| − | + | $$ | |
| + | \phi _ {i} (v) = \sum _ {S \subset N } \gamma _ {n} (s) | ||
| + | [ v (S) -v ( S \setminus \{ i \} ) ] , | ||
| + | $$ | ||
| − | + | $ \gamma _ {n} (s) = (s-1) ! (n-s) ! / n ! $ | |
| + | and $ s $ | ||
| + | is the number of elements of the set $ S $, | ||
| + | also satisfies the axiom of symmetry, but, moreover, $ \sum _ {i} \phi _ {i} (v) = v (N) $, | ||
| + | and for any two games $ u $ | ||
| + | and $ v $ | ||
| + | the equality $ \phi (u+v) = \phi (u) + \phi (v) $ | ||
| + | holds. Arbitration schemes with interpersonal utility comparisons have also been considered [[#References|[3]]]. | ||
| − | is also a solution if and only if | + | The arbitration schemes of Nash and Shapley were generalized by J.C. Harsanyi [[#References|[4]]]. A Harsanyi solution satisfies, apart from the four axioms of Nash, the two axioms: 1) the solution depends monotonically on the initial demands of the players; and 2) if $ u ^ {*} $ |
| + | and $ u ^ {**} $ | ||
| + | are two solutions, then $ \overline{u}\; $, | ||
| + | defined by | ||
| + | |||
| + | $$ | ||
| + | \overline{u}\; \geq \mathop{\rm min} _ {i \in N } | ||
| + | ( u _ {i} ^ {*} , u _ {i} ^ {**} ) , | ||
| + | $$ | ||
| + | |||
| + | is also a solution if and only if $ \overline{u}\; $ | ||
| + | belongs to the boundary of the set $ R $. | ||
Under suitable conditions an arbitration scheme depends continuously on the parameters of the game. | Under suitable conditions an arbitration scheme depends continuously on the parameters of the game. | ||
| Line 21: | Line 78: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Nash, "The bargaining problem" ''Econometrica'' , '''18''' : 2 (1950) pp. 155–162</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.S. Shapley, "A value for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013050/a01305041.png" />-person games" H.W. Kuhn (ed.) A.W. Tucker (ed.) M. Dresher (ed.) , ''Contributions to the theory of games'' , '''2''' , Princeton Univ. Press (1953) pp. 307–317</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H. Raiffa, "Arbitration schemes for generalized two-person games" H.W. Kuhn (ed.) A.W. Tucker (ed.) M. Dresher (ed.) , ''Contributions to the theory of games'' , '''2''' , Princeton Univ. Press (1953) pp. 361–387</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J.C. Harsanyi, "A bargaining model for the cooperative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013050/a01305042.png" />-person game" H.W. Kuhn (ed.) A.W. Tucker (ed.) M. Dresher (ed.) , ''Contributions to the theory of games'' , '''4''' , Princeton Univ. Press (1959) pp. 325–355</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Nash, "The bargaining problem" ''Econometrica'' , '''18''' : 2 (1950) pp. 155–162</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.S. Shapley, "A value for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013050/a01305041.png" />-person games" H.W. Kuhn (ed.) A.W. Tucker (ed.) M. Dresher (ed.) , ''Contributions to the theory of games'' , '''2''' , Princeton Univ. Press (1953) pp. 307–317</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H. Raiffa, "Arbitration schemes for generalized two-person games" H.W. Kuhn (ed.) A.W. Tucker (ed.) M. Dresher (ed.) , ''Contributions to the theory of games'' , '''2''' , Princeton Univ. Press (1953) pp. 361–387</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J.C. Harsanyi, "A bargaining model for the cooperative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013050/a01305042.png" />-person game" H.W. Kuhn (ed.) A.W. Tucker (ed.) M. Dresher (ed.) , ''Contributions to the theory of games'' , '''4''' , Princeton Univ. Press (1959) pp. 325–355</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | Arbitration schemes are also called bargaining schemes and a Nash solution is also called a bargaining solution. The Shapley solution vector | + | Arbitration schemes are also called bargaining schemes and a Nash solution is also called a bargaining solution. The Shapley solution vector $ \phi $ |
| + | is also called the [[Shapley value]]. For other, more recent, bargaining schemes, such as the Kalai–Smorodinsky solution and Szidarovsky's generalization of the concept of a Nash solution, the reader is referred to [[#References|[a1]]], [[#References|[a2]]], respectively [[#References|[a6]]]. For further developments concerning Harsanyi solutions, cf. [[#References|[a3]]]. Some authors distinguish between bargaining schemes and arbitration schemes. Then the Nash scheme is a bargaining scheme and the Shapley one an arbitration scheme, [[#References|[a5]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Kalai, M. Smorodinsky, "Other solutions to Nash's bargaining problems" ''Econometrica'' , '''43''' (1975) pp. 513–518</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.E. Roth, "Axiomatic models of bargaining" , ''Lect. notes econom. and math. systems'' , '''170''' , Springer (1979)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.C. Harsanyi, "Papers in game theory" , Reidel (1982)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> R.J. Aumann, L.S. Shapley, "Values of non-atomic games" , Princeton Univ. Press (1974)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> A. Rapoport, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013050/a01305044.png" />-person game theory: Concepts and applications" , Univ. Michigan Press (1970) pp. 168</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> J. Szép, F. Forgó, "Introduction to the theory of games" , Reidel (1985) pp. 171; 199</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> N.N. Vorob'ev, "Game theory. Lectures for economists and system scientists" , Springer (1977) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Kalai, M. Smorodinsky, "Other solutions to Nash's bargaining problems" ''Econometrica'' , '''43''' (1975) pp. 513–518</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.E. Roth, "Axiomatic models of bargaining" , ''Lect. notes econom. and math. systems'' , '''170''' , Springer (1979)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.C. Harsanyi, "Papers in game theory" , Reidel (1982)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> R.J. Aumann, L.S. Shapley, "Values of non-atomic games" , Princeton Univ. Press (1974)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> A. Rapoport, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013050/a01305044.png" />-person game theory: Concepts and applications" , Univ. Michigan Press (1970) pp. 168</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> J. Szép, F. Forgó, "Introduction to the theory of games" , Reidel (1985) pp. 171; 199</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> N.N. Vorob'ev, "Game theory. Lectures for economists and system scientists" , Springer (1977) (Translated from Russian)</TD></TR></table> | ||
Revision as of 18:48, 5 April 2020
A rule by which each arbitration game (cf. Cooperative game) is put into correspondence with a unique outcome of the game is called an arbitration solution. The first arbitration scheme was considered by J. Nash [1] for the case of a two-person game. Let $ R= \{ u = ( u _ {1} \dots u _ {n} ) \} $
be the set of outcomes, let $ d = ( d _ {1} \dots d _ {n} ) $
be the status quo point, i.e. the point corresponding to the situation in which no cooperative outcome is realized, let $ [ R, d ] $
be the corresponding arbitration game and let $ \overline{u}\; $
be an arbitration solution of it. An outcome $ u ^ {*} $
is called a Nash solution if
$$ \prod _ { i } ( u _ {i} ^ {*} - d _ {i} ) = \max _ {u \in R } \prod _ { i } ( u _ {i} - d _ {i} ) . $$
Only a Nash solution satisfies the following axioms: 1) if $ f $ is a linear non-decreasing mapping then $ f \overline{u}\; $ is an arbitration solution of the game $ [ fR, fd ] $( invariance with respect to utility transformations); 2) $ \overline{u}\; \geq d $, $ \overline{u}\; \in R $ and there is no $ u \in R $ such that $ u \geq \overline{u}\; $( Pareto optimality); 3) if $ R ^ \prime \subset R $, $ d ^ \prime = d $, $ \overline{u}\; \in R ^ \prime $, then $ \overline{u}\; {} ^ \prime = \overline{u}\; $( independence of irrelevant alternatives); and 4) if $ d _ {i} = d _ {j} $, $ i, j = 1 \dots n $, and $ R $ is symmetric, then $ \overline{u}\; _ {i} = \overline{u}\; _ {j} $, $ i, j = 1 \dots n $( symmetry).
Another arbitration scheme for an $ n $- person game with characteristic function $ v $ and player set $ N = \{ 1 \dots n \} $ was given by L.S. Shapley [2]. The Shapley solution $ \phi (v) = ( \phi _ {1} (v) \dots \phi _ {n} (v) ) $, where
$$ \phi _ {i} (v) = \sum _ {S \subset N } \gamma _ {n} (s) [ v (S) -v ( S \setminus \{ i \} ) ] , $$
$ \gamma _ {n} (s) = (s-1) ! (n-s) ! / n ! $ and $ s $ is the number of elements of the set $ S $, also satisfies the axiom of symmetry, but, moreover, $ \sum _ {i} \phi _ {i} (v) = v (N) $, and for any two games $ u $ and $ v $ the equality $ \phi (u+v) = \phi (u) + \phi (v) $ holds. Arbitration schemes with interpersonal utility comparisons have also been considered [3].
The arbitration schemes of Nash and Shapley were generalized by J.C. Harsanyi [4]. A Harsanyi solution satisfies, apart from the four axioms of Nash, the two axioms: 1) the solution depends monotonically on the initial demands of the players; and 2) if $ u ^ {*} $ and $ u ^ {**} $ are two solutions, then $ \overline{u}\; $, defined by
$$ \overline{u}\; \geq \mathop{\rm min} _ {i \in N } ( u _ {i} ^ {*} , u _ {i} ^ {**} ) , $$
is also a solution if and only if $ \overline{u}\; $ belongs to the boundary of the set $ R $.
Under suitable conditions an arbitration scheme depends continuously on the parameters of the game.
References
| [1] | J. Nash, "The bargaining problem" Econometrica , 18 : 2 (1950) pp. 155–162 |
| [2] | L.S. Shapley, "A value for  -person games" H.W. Kuhn (ed.) A.W. Tucker (ed.) M. Dresher (ed.) , Contributions to the theory of games , 2 , Princeton Univ. Press (1953) pp. 307–317 -person games" H.W. Kuhn (ed.) A.W. Tucker (ed.) M. Dresher (ed.) , Contributions to the theory of games , 2 , Princeton Univ. Press (1953) pp. 307–317 |
| [3] | H. Raiffa, "Arbitration schemes for generalized two-person games" H.W. Kuhn (ed.) A.W. Tucker (ed.) M. Dresher (ed.) , Contributions to the theory of games , 2 , Princeton Univ. Press (1953) pp. 361–387 |
| [4] | J.C. Harsanyi, "A bargaining model for the cooperative  -person game" H.W. Kuhn (ed.) A.W. Tucker (ed.) M. Dresher (ed.) , Contributions to the theory of games , 4 , Princeton Univ. Press (1959) pp. 325–355 -person game" H.W. Kuhn (ed.) A.W. Tucker (ed.) M. Dresher (ed.) , Contributions to the theory of games , 4 , Princeton Univ. Press (1959) pp. 325–355 |
Comments
Arbitration schemes are also called bargaining schemes and a Nash solution is also called a bargaining solution. The Shapley solution vector $ \phi $ is also called the Shapley value. For other, more recent, bargaining schemes, such as the Kalai–Smorodinsky solution and Szidarovsky's generalization of the concept of a Nash solution, the reader is referred to [a1], [a2], respectively [a6]. For further developments concerning Harsanyi solutions, cf. [a3]. Some authors distinguish between bargaining schemes and arbitration schemes. Then the Nash scheme is a bargaining scheme and the Shapley one an arbitration scheme, [a5].
References
| [a1] | E. Kalai, M. Smorodinsky, "Other solutions to Nash's bargaining problems" Econometrica , 43 (1975) pp. 513–518 |
| [a2] | A.E. Roth, "Axiomatic models of bargaining" , Lect. notes econom. and math. systems , 170 , Springer (1979) |
| [a3] | J.C. Harsanyi, "Papers in game theory" , Reidel (1982) |
| [a4] | R.J. Aumann, L.S. Shapley, "Values of non-atomic games" , Princeton Univ. Press (1974) |
| [a5] | A. Rapoport, "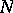 -person game theory: Concepts and applications" , Univ. Michigan Press (1970) pp. 168 -person game theory: Concepts and applications" , Univ. Michigan Press (1970) pp. 168 |
| [a6] | J. Szép, F. Forgó, "Introduction to the theory of games" , Reidel (1985) pp. 171; 199 |
| [a7] | N.N. Vorob'ev, "Game theory. Lectures for economists and system scientists" , Springer (1977) (Translated from Russian) |
Arbitration scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Arbitration_scheme&oldid=45209