Difference between revisions of "Arakelov geometry"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (link) |
||
| Line 29: | Line 29: | ||
<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024051.png" />, give rise to arithmetic intersection numbers, which are real numbers when their geometric counterparts are integers. Examples of such real numbers are the heights of points and subvarieties, for which Arakelov geometry provides a useful framework [[#References|[a3]]]. | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024051.png" />, give rise to arithmetic intersection numbers, which are real numbers when their geometric counterparts are integers. Examples of such real numbers are the heights of points and subvarieties, for which Arakelov geometry provides a useful framework [[#References|[a3]]]. | ||
| − | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024052.png" /> is a semi-stable arithmetic surface, an important invariant of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024053.png" /> is the self-intersection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024054.png" /> of the relative dualizing sheaf equipped with the Arakelov metric [[#References|[a1]]]. L. Szpiro and A.N. Parshin have shown that a good upper bound for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024055.png" /> would lead to an effective version of the Mordell conjecture and to a solution of the | + | When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024052.png" /> is a semi-stable arithmetic surface, an important invariant of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024053.png" /> is the self-intersection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024054.png" /> of the relative dualizing sheaf equipped with the Arakelov metric [[#References|[a1]]]. L. Szpiro and A.N. Parshin have shown that a good upper bound for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024055.png" /> would lead to an effective version of the Mordell conjecture and to a solution of the [[ABC conjecture]] [[#References|[a10]]]. G. Faltings and E. Ullmo proved that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024056.png" /> is strictly positive [[#References|[a4]]], [[#References|[a11]]]; this implies that the set of algebraic points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024057.png" /> is discrete in its Jacobian for the topology given by the Néron–Tate height. |
P. Vojta used Arakelov geometry to give a new proof of the Mordell conjecture [[#References|[a12]]], by adapting the method of Diophantine approximation. More generally, Faltings obtained by Vojta's method a proof of a conjecture of S. Lang on Abelian varieties [[#References|[a5]]]: Assume <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024058.png" /> is an [[Abelian variety|Abelian variety]] over a number field and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024059.png" /> be a proper closed subvariety in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024060.png" />; then the set of rational points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024061.png" /> is contained in the union of finitely many translates of Abelian proper subvarieties of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024062.png" />. | P. Vojta used Arakelov geometry to give a new proof of the Mordell conjecture [[#References|[a12]]], by adapting the method of Diophantine approximation. More generally, Faltings obtained by Vojta's method a proof of a conjecture of S. Lang on Abelian varieties [[#References|[a5]]]: Assume <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024058.png" /> is an [[Abelian variety|Abelian variety]] over a number field and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024059.png" /> be a proper closed subvariety in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024060.png" />; then the set of rational points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024061.png" /> is contained in the union of finitely many translates of Abelian proper subvarieties of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a120/a120240/a12024062.png" />. | ||
Revision as of 20:00, 6 September 2013
Arakelov theory
A combination of the Grothendieck algebraic geometry of schemes over  with Hermitian complex geometry on their set of complex points. The goal is to provide a geometric framework for the study of Diophantine problems in higher dimension (cf. also Diophantine equations, solvability problem of; Diophantine problems of additive type).
with Hermitian complex geometry on their set of complex points. The goal is to provide a geometric framework for the study of Diophantine problems in higher dimension (cf. also Diophantine equations, solvability problem of; Diophantine problems of additive type).
The construction relies upon the analogy between number fields and function fields: the ring  has Krull dimension (cf. Dimension) one, and "adding a point"
has Krull dimension (cf. Dimension) one, and "adding a point"  to the corresponding scheme
to the corresponding scheme  makes it look like a complete curve. For instance, if
makes it look like a complete curve. For instance, if  is a rational number, the identity
is a rational number, the identity
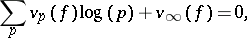 |
where  is the valuation of
is the valuation of  at the prime
at the prime  and where
and where  , is similar to the Cauchy residue formula
, is similar to the Cauchy residue formula
 |
for the differential 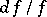 , when
, when  is a non-zero rational function on a smooth complex projective curve
is a non-zero rational function on a smooth complex projective curve  .
.
In higher dimension, given a regular projective flat scheme 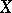 over
over 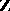 , one considers pairs
, one considers pairs 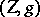 consisting of an algebraic cycle
consisting of an algebraic cycle 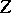 of codimension
of codimension 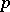 over
over 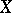 , together with a Green current
, together with a Green current 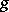 for
for 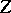 on the complex manifold
on the complex manifold 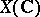 :
: 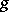 is real current of type
is real current of type  such that, if
such that, if 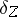 denotes the current given by integration on
denotes the current given by integration on 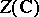 , the following equality of currents holds:
, the following equality of currents holds:
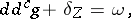 |
where  is a smooth form of type
is a smooth form of type 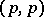 . Equivalence classes of such pairs
. Equivalence classes of such pairs 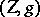 form the arithmetic Chow group
form the arithmetic Chow group  , which has good functoriality properties and is equipped with a graded intersection product, at least after tensoring it by
, which has good functoriality properties and is equipped with a graded intersection product, at least after tensoring it by 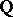 .
.
These notions were first introduced for arithmetic surfaces, i.e. models of curves over number fields [a1], [a2] (for a restricted class of currents 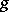 ). For the general theory, see [a7], [a9] and references therein.
). For the general theory, see [a7], [a9] and references therein.
Given a pair  consisting of an algebraic vector bundle
consisting of an algebraic vector bundle 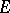 on
on 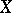 and a
and a  Hermitian metric
Hermitian metric 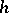 on the corresponding holomorphic vector bundle on the complex-analytic manifold
on the corresponding holomorphic vector bundle on the complex-analytic manifold 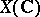 , one can define characteristic classes of
, one can define characteristic classes of 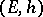 with values in the arithmetic Chow groups of
with values in the arithmetic Chow groups of 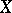 . For instance, when
. For instance, when  has rank one, if
has rank one, if  is a non-zero rational section of
is a non-zero rational section of 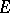 and
and 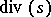 its divisor, the first Chern class of
its divisor, the first Chern class of 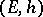 is the class of the pair
is the class of the pair 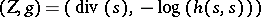 . The main result of the theory is the arithmetic Riemann–Roch theorem, which computes the behaviour of the Chern character under direct image [a8], [a6]. Its strongest version involves regularized determinants of Laplace operators and the proof requires hard analytic work, due to J.-M. Bismut and others.
. The main result of the theory is the arithmetic Riemann–Roch theorem, which computes the behaviour of the Chern character under direct image [a8], [a6]. Its strongest version involves regularized determinants of Laplace operators and the proof requires hard analytic work, due to J.-M. Bismut and others.
Since 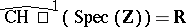 , the pairings
, the pairings
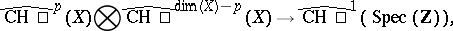 |
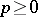 , give rise to arithmetic intersection numbers, which are real numbers when their geometric counterparts are integers. Examples of such real numbers are the heights of points and subvarieties, for which Arakelov geometry provides a useful framework [a3].
, give rise to arithmetic intersection numbers, which are real numbers when their geometric counterparts are integers. Examples of such real numbers are the heights of points and subvarieties, for which Arakelov geometry provides a useful framework [a3].
When 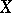 is a semi-stable arithmetic surface, an important invariant of
is a semi-stable arithmetic surface, an important invariant of 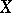 is the self-intersection
is the self-intersection 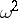 of the relative dualizing sheaf equipped with the Arakelov metric [a1]. L. Szpiro and A.N. Parshin have shown that a good upper bound for
of the relative dualizing sheaf equipped with the Arakelov metric [a1]. L. Szpiro and A.N. Parshin have shown that a good upper bound for 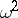 would lead to an effective version of the Mordell conjecture and to a solution of the ABC conjecture [a10]. G. Faltings and E. Ullmo proved that
would lead to an effective version of the Mordell conjecture and to a solution of the ABC conjecture [a10]. G. Faltings and E. Ullmo proved that 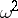 is strictly positive [a4], [a11]; this implies that the set of algebraic points of
is strictly positive [a4], [a11]; this implies that the set of algebraic points of 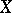 is discrete in its Jacobian for the topology given by the Néron–Tate height.
is discrete in its Jacobian for the topology given by the Néron–Tate height.
P. Vojta used Arakelov geometry to give a new proof of the Mordell conjecture [a12], by adapting the method of Diophantine approximation. More generally, Faltings obtained by Vojta's method a proof of a conjecture of S. Lang on Abelian varieties [a5]: Assume  is an Abelian variety over a number field and let
is an Abelian variety over a number field and let  be a proper closed subvariety in
be a proper closed subvariety in  ; then the set of rational points of
; then the set of rational points of 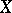 is contained in the union of finitely many translates of Abelian proper subvarieties of
is contained in the union of finitely many translates of Abelian proper subvarieties of 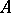 .
.
See also Diophantine geometry; Height, in Diophantine geometry; Mordell conjecture.
References
| [a1] | S.J. Arakelov, "Intersection theory of divisors on an arithmetic surface" Math. USSR Izv. , 8 (1974) pp. 1167–1180 MR472815 Zbl 0355.14002 |
| [a2] | S.J. Arakelov, "Theory of intersections on an arithmetic surface" , Proc. Internat. Congr. Mathematicians Vancouver , 1 , Amer. Math. Soc. (1975) pp. 405–408 MR466150 |
| [a3] | J.-B. Bost, H. Gillet, C. Soulé, "Heights of projective varieties and positive Green forms" J. Amer. Math. Soc. , 7 (1994) pp. 903–1027 MR1260106 Zbl 0973.14013 |
| [a4] | G. Faltings, "Calculus on arithmetic surfaces" Ann. of Math. , 119 (1984) pp. 387–424 MR0740897 Zbl 0559.14005 |
| [a5] | G. Faltings, "Diophantine approximation on Abelian varieties" Ann. of Math. , 133 (1991) pp. 549–576 MR1109353 Zbl 0734.14007 |
| [a6] | G. Faltings, "Lectures on the arithmetic Riemann–Roch theorem" Ann. Math. Study , 127 (1992) (Notes by S. Zhang) MR1158661 Zbl 0744.14016 |
| [a7] | H. Gillet, C. Soulé, "Arithmetic intersection theory" Publ. Math. IHES , 72 (1990) pp. 94–174 MR1087394 Zbl 0741.14012 |
| [a8] | H. Gillet, C. Soulé, "An arithmetic Riemann–Roch Theorem" Invent. Math. , 110 (1992) pp. 473–543 MR1189489 Zbl 0777.14008 |
| [a9] | C. Soulé, D. Abramovich, J.-F. Burnol, J. Kramer, "Lectures on Arakelov geometry" , Studies Adv. Math. , 33 , Cambridge Univ. Press (1992) MR1208731 Zbl 0812.14015 |
| [a10] | L. Szpiro, "Séminaire sur les pinceaux de courbes elliptiques (à la recherche de Mordell effectif)" Astérisque , 183 (1990) |
| [a11] | E. Ullmo, "Positivité et discrétion des points algébriques des courbes" Ann. of Math. , 147 : 1 (1998) pp. 167–179 MR1609514 Zbl 0934.14013 |
| [a12] | P. Vojta, "Siegel's theorem in the compact case" Ann. of Math. , 133 (1991) pp. 509–548 MR1109352 |
Arakelov geometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Arakelov_geometry&oldid=30390