Andronov-Witt theorem
A modification of Lyapunov's theorem (on the stability of a periodic solution of a non-autonomous system of differential equations) for the autonomous system
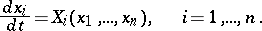 | (1) |
Let
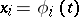 | (2) |
be a periodic solution of the system (1), and let
 | (3) |
be the corresponding system of variational equations which always has, in the case here considered, one zero characteristic exponent. The Andronov–Witt theorem is then valid: If 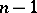 characteristic exponents of the system (3) have negative real parts, a periodic solution (2) of the system (1) is stable according to Lyapunov (cf. Lyapunov characteristic exponent; Lyapunov stability).
characteristic exponents of the system (3) have negative real parts, a periodic solution (2) of the system (1) is stable according to Lyapunov (cf. Lyapunov characteristic exponent; Lyapunov stability).
The Andronov–Witt theorem was first formulated by A.A. Andronov and A.A. Witt in 1930 and was proved by them in 1933 [1].
References
| [1] | A.A. Andronov, "Collected works" , Moscow (1976) (In Russian) |
| [2] | L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) pp. 264 (Translated from Russian) |
Comments
The Andronov–Witt theorem is usually found in the Western literature under some heading like "hyperbolic periodic attractorhyperbolic periodic attractor" .
Good additional general references are [a1], [a2], [a3]. In [a2] the theorem under discussion occurs as a statement about periodic attractors, cf. pp. 277-278. The original Andronov–Witt paper is [a4].
References
| [a1] | W. Hahn, "Stability of motion" , Springer (1967) pp. 422 |
| [a2] | M.W. Hirsch, S. Smale, "Differential equations, dynamic systems and linear algebra" , Acad. Press (1974) |
| [a3] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. 323 |
| [a4] | A.A. Andronov, A. Witt, "Zur Stabilität nach Liapounov" Physikal. Z. Sowjetunion , 4 (1933) pp. 606–608 |
Andronov-Witt theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Andronov-Witt_theorem&oldid=15354