Difference between revisions of "Alternating-direction implicit method"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | a1105401.png | ||
| + | $#A+1 = 31 n = 1 | ||
| + | $#C+1 = 31 : ~/encyclopedia/old_files/data/A110/A.1100540 Alternating\AAhdirection implicit method | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A method introduced in 1955 by D.W. Peaceman and H.H. Rachford [[#References|[a3]]] and J. Douglas [[#References|[a1]]] as a technique for the numerical solution of elliptic and parabolic differential equations (cf. [[Elliptic partial differential equation|Elliptic partial differential equation]]; [[Parabolic partial differential equation|Parabolic partial differential equation]]). Let $ \Omega \in \mathbf R ^ {2} $ | |
| + | be a bounded region and $ K _ {1} ,K _ {2} , K _ {0} $ | ||
| + | continuous functions with $ K _ {1} ( x,y ) > 0 $, | ||
| + | $ K _ {2} ( x,y ) > 0 $, | ||
| + | $ K _ {0} ( x,y ) \geq 0 $ | ||
| + | in $ \Omega $. | ||
| + | The discretization of the elliptic boundary value problem (cf. [[Boundary value problem, elliptic equations|Boundary value problem, elliptic equations]]) | ||
| − | + | $$ | |
| + | - ( K _ {1} u _ {x} ) _ {x} - ( K _ {2} u _ {y} ) _ {y} + K _ {0} u = f \textrm{ in } \Omega, | ||
| + | $$ | ||
| − | + | $$ | |
| + | u = g \textrm{ on } \partial \Omega, | ||
| + | $$ | ||
| − | + | in a bounded region $ \Omega \subset \mathbf R ^ {2} $ | |
| + | by finite differences leads to a system of linear equations of the form | ||
| − | + | $$ | |
| + | ( H + V + S ) \mathbf u = \mathbf f . | ||
| + | $$ | ||
| − | + | Here, the matrices $ H $ | |
| + | and $ V $ | ||
| + | stand for the discretization of the differential operators in the $ x $( | ||
| + | horizontal) and $ y $( | ||
| + | vertical) direction, respectively, and $ S $ | ||
| + | is a diagonal matrix representing multiplication by $ K _ {0} $. | ||
| + | The alternating-direction implicit method attempts to solve this linear system by the iteration | ||
| − | with some parameters | + | $$ |
| + | \left ( H + { | ||
| + | \frac{1}{2} | ||
| + | } S + \rho _ {k} I \right ) \mathbf u _ {k - {1 / 2 } } = \left ( \rho _ {k} I - V - { | ||
| + | \frac{1}{2} | ||
| + | } S \right ) \mathbf u _ {k - 1 } + \mathbf f, | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | \left ( V + { | ||
| + | \frac{1}{2} | ||
| + | } S + \rho _ {k} I \right ) \mathbf u _ {k} = \left ( \rho _ {k} I - H - { | ||
| + | \frac{1}{2} | ||
| + | } S \right ) \mathbf u _ {k - {1 / 2 } } + \mathbf f, k = 1, 2, \dots, | ||
| + | $$ | ||
| + | |||
| + | with some parameters $ \rho _ {k} > 0 $. | ||
| + | On a uniform mesh, each of the two half-steps in the above iteration scheme requires the solution of a number of tri-diagonal systems arising from one-dimensional difference operators, a task which is relatively inexpensive. On an $ n $ | ||
| + | by $ n $ | ||
| + | rectangular mesh, the appropriate choice of a set of parameters $ \rho _ {1} \dots \rho _ {l} $( | ||
| + | with $ l = { \mathop{\rm log} } n $) | ||
| + | in the above iteration allows one to solve the [[Poisson equation|Poisson equation]] ( $ K _ {1} = K _ {2} \equiv 1 $, | ||
| + | $ K _ {0} = 0 $) | ||
| + | with an operation count of $ O ( n ^ {2} { \mathop{\rm log} } n ) $, | ||
| + | which is almost optimal. (Optimal methods with an operation count proportional to the number of unknowns $ n ^ {2} $ | ||
| + | have later been developed using multi-grid methods.) | ||
For the parabolic initial-boundary value problem | For the parabolic initial-boundary value problem | ||
| − | + | $$ | |
| + | u _ {t} = ( K _ {1} u _ {x} ) _ {x} + ( K _ {2} u _ {y} ) _ {y} + K _ {0} u = f \textrm{ in } ( 0,T ) \times \Omega, | ||
| + | $$ | ||
| − | + | $$ | |
| + | u = g \textrm{ on } ( 0,T ) \times \partial \Omega, u = u _ {0} \textrm{ for } t = 0, | ||
| + | $$ | ||
| − | implicit discretization in time requires the solution of an elliptic boundary value problem of the type above in each time-step. The alternating-direction implicit method advances in time by inverting only the one-dimensional difference operators in | + | implicit discretization in time requires the solution of an elliptic boundary value problem of the type above in each time-step. The alternating-direction implicit method advances in time by inverting only the one-dimensional difference operators in $ x $- |
| + | and in $ y $- | ||
| + | direction. Each time step is therefore much less expensive. It can be shown to be unconditionally stable. The classical reference is [[#References|[a4]]], Chapts. 7, 8. | ||
In the 1980{}s, the apparent potential for parallelism in the alternating-direction implicit method led to research on the appropriate implementation on parallel computers [[#References|[a2]]]. | In the 1980{}s, the apparent potential for parallelism in the alternating-direction implicit method led to research on the appropriate implementation on parallel computers [[#References|[a2]]]. | ||
Revision as of 16:10, 1 April 2020
A method introduced in 1955 by D.W. Peaceman and H.H. Rachford [a3] and J. Douglas [a1] as a technique for the numerical solution of elliptic and parabolic differential equations (cf. Elliptic partial differential equation; Parabolic partial differential equation). Let $ \Omega \in \mathbf R ^ {2} $
be a bounded region and $ K _ {1} ,K _ {2} , K _ {0} $
continuous functions with $ K _ {1} ( x,y ) > 0 $,
$ K _ {2} ( x,y ) > 0 $,
$ K _ {0} ( x,y ) \geq 0 $
in $ \Omega $.
The discretization of the elliptic boundary value problem (cf. Boundary value problem, elliptic equations)
$$ - ( K _ {1} u _ {x} ) _ {x} - ( K _ {2} u _ {y} ) _ {y} + K _ {0} u = f \textrm{ in } \Omega, $$
$$ u = g \textrm{ on } \partial \Omega, $$
in a bounded region $ \Omega \subset \mathbf R ^ {2} $ by finite differences leads to a system of linear equations of the form
$$ ( H + V + S ) \mathbf u = \mathbf f . $$
Here, the matrices $ H $ and $ V $ stand for the discretization of the differential operators in the $ x $( horizontal) and $ y $( vertical) direction, respectively, and $ S $ is a diagonal matrix representing multiplication by $ K _ {0} $. The alternating-direction implicit method attempts to solve this linear system by the iteration
$$ \left ( H + { \frac{1}{2} } S + \rho _ {k} I \right ) \mathbf u _ {k - {1 / 2 } } = \left ( \rho _ {k} I - V - { \frac{1}{2} } S \right ) \mathbf u _ {k - 1 } + \mathbf f, $$
$$ \left ( V + { \frac{1}{2} } S + \rho _ {k} I \right ) \mathbf u _ {k} = \left ( \rho _ {k} I - H - { \frac{1}{2} } S \right ) \mathbf u _ {k - {1 / 2 } } + \mathbf f, k = 1, 2, \dots, $$
with some parameters $ \rho _ {k} > 0 $. On a uniform mesh, each of the two half-steps in the above iteration scheme requires the solution of a number of tri-diagonal systems arising from one-dimensional difference operators, a task which is relatively inexpensive. On an $ n $ by $ n $ rectangular mesh, the appropriate choice of a set of parameters $ \rho _ {1} \dots \rho _ {l} $( with $ l = { \mathop{\rm log} } n $) in the above iteration allows one to solve the Poisson equation ( $ K _ {1} = K _ {2} \equiv 1 $, $ K _ {0} = 0 $) with an operation count of $ O ( n ^ {2} { \mathop{\rm log} } n ) $, which is almost optimal. (Optimal methods with an operation count proportional to the number of unknowns $ n ^ {2} $ have later been developed using multi-grid methods.)
For the parabolic initial-boundary value problem
$$ u _ {t} = ( K _ {1} u _ {x} ) _ {x} + ( K _ {2} u _ {y} ) _ {y} + K _ {0} u = f \textrm{ in } ( 0,T ) \times \Omega, $$
$$ u = g \textrm{ on } ( 0,T ) \times \partial \Omega, u = u _ {0} \textrm{ for } t = 0, $$
implicit discretization in time requires the solution of an elliptic boundary value problem of the type above in each time-step. The alternating-direction implicit method advances in time by inverting only the one-dimensional difference operators in $ x $- and in $ y $- direction. Each time step is therefore much less expensive. It can be shown to be unconditionally stable. The classical reference is [a4], Chapts. 7, 8.
In the 1980{}s, the apparent potential for parallelism in the alternating-direction implicit method led to research on the appropriate implementation on parallel computers [a2].
References
| [a1] | J. Douglas, "On the numerical integration of 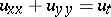 by implicit methods" SIAM J. , 3 (1962) pp. 42–65 by implicit methods" SIAM J. , 3 (1962) pp. 42–65 |
| [a2] | S. Lennart Johnsson, Y. Saad, M.H. Schultz, "Alternating direction methods on multiprocessors" SIAM J. Sci. Statist. Comput. , 8 (1987) pp. 686–700 |
| [a3] | D.W. Peaceman, H.H. Rachford, "The numerical solution of parabolic and elliptic differential equations" SIAM J. , 3 (1955) pp. 28–41 |
| [a4] | R.S. Varga, "Matrix iterative analysis" , Prentice-Hall (1962) |
Alternating-direction implicit method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Alternating-direction_implicit_method&oldid=14574