Algorithmic reducibility
One of the basic concepts in the theory of algorithms (cf. Algorithms, theory of) and its applications. Its background was the fact that solvability (and unsolvability) of many algorithmic problems (cf. Algorithmic problem) is not established directly, but rather by reducing some algorithmic problem, already demonstrated to be unsolvable, to the problem in question, or by reducing the latter problem to some other one which has already been solved. Thus, the problem of homotopy of paths in a polyhedron is shown to be unsolvable by reducing the problem of equality of words in the corresponding fundamental group to this problem.
In what follows, the simplest examples of algorithmic reducibility of number-theoretical predicates and functions (i.e. those defined on natural numbers) will be presented:
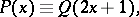 |
where 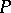 and
and 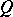 are predicates. The problem of solving the predicate
are predicates. The problem of solving the predicate 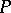 , that is, of establishing the truth or falsehood of
, that is, of establishing the truth or falsehood of 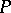 for different values of
for different values of  , is reduced to the problem of solving
, is reduced to the problem of solving 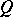 — or, "P is reduced to Q" , for short. One may also say that the set of truths of
— or, "P is reduced to Q" , for short. One may also say that the set of truths of 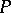 , i.e.
, i.e. 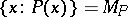 , is reduced to
, is reduced to 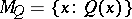 .
.
Let
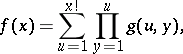 |
where 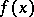 and
and 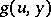 are number-theoretic functions. The problem of computation of the function
are number-theoretic functions. The problem of computation of the function  is reduced to the computation of
is reduced to the computation of 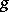 or, for short,
or, for short, 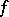 is reduced to
is reduced to 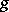 .
.
The concept of algorithmic reducibility was given a more exact form by A.M. Turing: If, roughly speaking, some Turing machine transforms a sequence of encoded values of the function 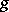 into a sequence of encoded values of the function
into a sequence of encoded values of the function 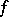 , then
, then 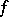 is reduced to
is reduced to 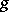 . S.C. Kleene [1] formulated the related concept of relative computability with the aid of recursive systems of equations. After arithmetization, each algorithmic problem is reduced to the problem of computing some number-theoretic function
. S.C. Kleene [1] formulated the related concept of relative computability with the aid of recursive systems of equations. After arithmetization, each algorithmic problem is reduced to the problem of computing some number-theoretic function 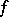 . If
. If 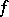 is reduced to
is reduced to 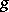 according to Turing,
according to Turing, 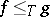 , and
, and 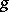 is reduced to
is reduced to 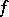 ,
, 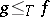 , then one says that
, then one says that 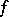 and
and  have the same degree of unsolvability or that
have the same degree of unsolvability or that  . The relation
. The relation  is both reflexive and transitive. Thus, all functions (and sets of natural numbers or their characteristic predicates) are subdivided into equivalence classes, known as Turing degrees or
is both reflexive and transitive. Thus, all functions (and sets of natural numbers or their characteristic predicates) are subdivided into equivalence classes, known as Turing degrees or 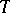 -degrees [3]. Most algorithmic problems considered in logic and in mathematics are expressible as problems of membership in enumerable sets of constructive objects. In this context the study of enumerable sets was initiated in the 1940s by E.L. Post [2]; he introduced certain special kinds of algorithmic reducibility, in addition to Turing's kind, and formulated the problem of reducibility as follows: Can various enumerable unsolvable sets be reduced (according to Turing) to each other? It was subsequently established that the enumerable sets form an infinite, very rich system of
-degrees [3]. Most algorithmic problems considered in logic and in mathematics are expressible as problems of membership in enumerable sets of constructive objects. In this context the study of enumerable sets was initiated in the 1940s by E.L. Post [2]; he introduced certain special kinds of algorithmic reducibility, in addition to Turing's kind, and formulated the problem of reducibility as follows: Can various enumerable unsolvable sets be reduced (according to Turing) to each other? It was subsequently established that the enumerable sets form an infinite, very rich system of 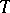 -degrees. This was supplemented by discovering the so-called priority method, which is extensively employed in the theory of algorithms.
-degrees. This was supplemented by discovering the so-called priority method, which is extensively employed in the theory of algorithms.
Subsequently, degrees of unsolvability found applications in other branches of mathematics as well. For instance, for all  -degrees
-degrees  and
and 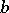 of enumerable sets, if
of enumerable sets, if 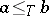 , then there exists a finitely-determined group in which the problem of equality of words has degree
, then there exists a finitely-determined group in which the problem of equality of words has degree  , while the conjugation problem has degree
, while the conjugation problem has degree 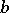 . There is a close connection between degrees (concerning the different kinds of algorithmic reducibility) of enumerable sets and the rate of growth of the complexity of initial fragments of enumerable sets. A special kind of reducibility — polynomial reducibility or p-reducibility (reducibility with some limitation imposed on time) — is employed in proving the universal character of combinatorial optimization problems from various branches of mathematics [5]; for more details on this subject see [1]. The methods of measure theory [1], and the forcing method [4] have in turn been used in the study of degrees.
. There is a close connection between degrees (concerning the different kinds of algorithmic reducibility) of enumerable sets and the rate of growth of the complexity of initial fragments of enumerable sets. A special kind of reducibility — polynomial reducibility or p-reducibility (reducibility with some limitation imposed on time) — is employed in proving the universal character of combinatorial optimization problems from various branches of mathematics [5]; for more details on this subject see [1]. The methods of measure theory [1], and the forcing method [4] have in turn been used in the study of degrees.
References
| [1] | H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967) |
| [2] | E.L. Post, "Recursively enumerable sets of positive integers and their decision problems" Bull. Amer. Math. Soc. , 50 (1944) pp. 284–316 |
| [3] | S.C. Kleene, E.L. Post, "The upper semi-lattice of degrees of recursive unsolvability" Ann. of Math. (2) , 59 : 3 (1954) pp. 379–407 |
| [4] | A.L. Selman, "Applications of forcing to the degree-theory of the arithmetical hierarchy" Proc. London Math. Soc. (3) , 25 (1972) pp. 586–602 |
| [5] | R.M. Karp, "Reducibility among combinatorial problems" R.E. Miller (ed.) J.W. Tatcher (ed.) , Complexity of Computer Computations. Proc. Symp. IBM , Plenum (85–103) |
Comments
References
| [a1] | R.I. Soare, "Recursively enumerable sets and degrees, a study of computable functions and generated sets" , Springer (1986) |
| [a2] | S.G. Simpson, "Degrees of unsolvability: a survey of results" J. Barwise (ed.) , Handbook of mathematical logic , North-Holland (1977) pp. 631–652 |
Algorithmic reducibility. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algorithmic_reducibility&oldid=15508