Algebraic variety, automorphism of an
An invertible morphism of an algebraic variety (or scheme) into itself. The group of all automorphisms of an algebraic variety 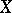 , which is usually denoted by
, which is usually denoted by 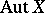 , is an important invariant of
, is an important invariant of 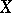 . Studies of the action of the automorphism group of an algebraic variety on objects functorially connected with
. Studies of the action of the automorphism group of an algebraic variety on objects functorially connected with 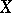 such as the Picard group; the Chow ring; the
such as the Picard group; the Chow ring; the 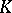 -functor, and the cohomology group are a tool used in the study of the varieties themselves. The automorphism group of an algebraic variety is important for the concept of forms (cf. Form) of an algebraic variety. For complete algebraic varieties over the field of complex numbers, the automorphism group is identical with the group of biholomorphic automorphisms.
-functor, and the cohomology group are a tool used in the study of the varieties themselves. The automorphism group of an algebraic variety is important for the concept of forms (cf. Form) of an algebraic variety. For complete algebraic varieties over the field of complex numbers, the automorphism group is identical with the group of biholomorphic automorphisms.
The structure of the group 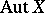 is known for a number of simple algebraic varieties. For instance, if
is known for a number of simple algebraic varieties. For instance, if 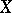 is projective
is projective  -dimensional space
-dimensional space  over a field
over a field 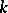 , then any one of its automorphisms is a linear projective transformation and
, then any one of its automorphisms is a linear projective transformation and 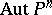 becomes identical with the projective linear group
becomes identical with the projective linear group 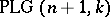 . The automorphism group of an elliptic curve and, in general, of any Abelian variety
. The automorphism group of an elliptic curve and, in general, of any Abelian variety 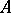 , is an extension of the group
, is an extension of the group 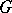 of automorphisms which preserve the structure of the Abelian variety, by the group
of automorphisms which preserve the structure of the Abelian variety, by the group 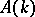 of translations in the points of
of translations in the points of 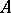 , i.e. the sequence of groups
, i.e. the sequence of groups
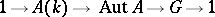 |
is exact. If 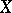 is a smooth, complete algebraic curve of genus
is a smooth, complete algebraic curve of genus 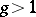 , then the group
, then the group 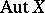 is finite; an estimate of its order as a function of
is finite; an estimate of its order as a function of 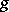 is known (cf. Algebraic curve). For automorphisms of surfaces, see Algebraic surface.
is known (cf. Algebraic curve). For automorphisms of surfaces, see Algebraic surface.
In the case of algebraic varieties with an ample canonical or anti-canonical invertible sheaf the automorphism group is an algebraic subgroup of the group 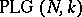 for some
for some 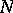 . The automorphism group of a smooth hypersurface of dimension
. The automorphism group of a smooth hypersurface of dimension 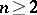 and degree
and degree 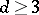 is finite [1].
is finite [1].
In the above examples, 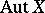 has the natural structure of an algebraic group, perhaps with an infinite number of connected components; this is also true in the general case [2].
has the natural structure of an algebraic group, perhaps with an infinite number of connected components; this is also true in the general case [2].
Families of automorphisms are considered in the modern approach to automorphism groups of algebraic varieties. A family of automorphisms of a variety 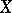 with parameter scheme
with parameter scheme 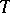 is a set of automorphisms of the product
is a set of automorphisms of the product 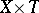 that commute with projection onto the second factor; the set of families of automorphisms with parameter scheme
that commute with projection onto the second factor; the set of families of automorphisms with parameter scheme 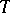 is denoted by
is denoted by 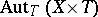 . One thus obtains a contravariant functor
. One thus obtains a contravariant functor 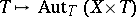 . If the variety
. If the variety 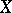 is complete, then this functor is locally representable (cf. Representable functor) by an algebraic group scheme with at most a countable number of connected components [3]. A. Grothendieck gave a proof of this fact for projective varieties, and this theorem has been extended to the case of proper flat schemes of morphisms. The scheme representing this functor is not necessarily reduced even if
is complete, then this functor is locally representable (cf. Representable functor) by an algebraic group scheme with at most a countable number of connected components [3]. A. Grothendieck gave a proof of this fact for projective varieties, and this theorem has been extended to the case of proper flat schemes of morphisms. The scheme representing this functor is not necessarily reduced even if 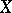 is a smooth projective surface; however, if the characteristic of the ground field is zero, or if
is a smooth projective surface; however, if the characteristic of the ground field is zero, or if 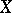 is a smooth curve or a smooth hypersurface, then the connected component of the unit of this scheme is a variety.
is a smooth curve or a smooth hypersurface, then the connected component of the unit of this scheme is a variety.
For incomplete varieties the automorphism functor is not always representable in the category of schemes. For an affine variety, the automorphism functor is representable in the category of inductive limits of schemes.
Apart from the simple case of the affine straight line, for the affine spaces only the automorphism group of the affine plane is known. It is a free product of two of its subgroups with as amalgamated subgroup their intersection, viz. the subgroup of linear affine transformations and the subgroup of triangular automorphisms, i.e. transformations of the form
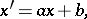 |
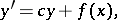 |
where  , while
, while 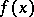 is an arbitrary polynomial in
is an arbitrary polynomial in  [4], [5]. For the treatment of affine algebraic surfaces transitively acted upon by the automorphism group, see [6].
[4], [5]. For the treatment of affine algebraic surfaces transitively acted upon by the automorphism group, see [6].
References
| [1] | H. Matsumura, P. Monsky, "On the automorphisms of hypersurfaces" J. Math. Kyoto Univ. , 3 (1964) pp. 347–361 MR0168559 Zbl 0141.37401 |
| [2] | T. Matsusaka, "Polarized varieties, fields of moduli and generalized Kummer varieties of polarized Abelian varieties" Amer. J. Math. , 80 (1958) pp. 45–82 MR0094360 Zbl 0085.15304 |
| [3] | H. Matsumura, F. Oort, "Representability of group functors and automorphisms of algebraic schemes" Invent. Math. , 4 (1967) pp. 1–25 MR0217090 |
| [4] | W. Engel, "Ganze Cremona-Transformationen von Primzahlgrad in der Ebene" Math. Ann. , 136 (1958) pp. 319–325 MR0103888 Zbl 0082.36502 |
| [5] | I.R. Shafarevich, "On some infinite-dimensional groups" Rend. di Mat. e Appl. , 25 (1966) pp. 208–212 MR0485898 Zbl 0149.39003 |
| [6] | M.Kh. Gizatullin, "Quasihomogeneous affine surfaces" Math. USSR-Izv. , 5 : 5 (1971) pp. 1057–1082 Izv. Akad. Nauk SSSR Ser. Mat. , 35 (1971) pp. 1047–1071 MR0286791 Zbl 0221.14023 |
| [7] | L. Roth, "Algebraic threefolds" , Springer (1955) MR0076426 Zbl 0066.14704 |
Algebraic variety, automorphism of an. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algebraic_variety,_automorphism_of_an&oldid=21794