Algebraic cycle
on an algebraic variety
An element of the free Abelian group the set of free generators of which is constituted by all closed irreducible subvarieties of the given algebraic variety. The subgroup of the group 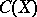 of algebraic cycles on a variety
of algebraic cycles on a variety 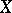 generated by a subvariety of codimension
generated by a subvariety of codimension 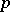 is denoted by
is denoted by 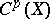 . The group
. The group 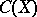 can be represented as the direct sum
can be represented as the direct sum
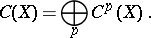 |
The subgroup 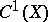 is identical with the group of Weil divisors (cf. Divisor) on
is identical with the group of Weil divisors (cf. Divisor) on 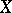 .
.
In what follows  will denote a non-singular projective algebraic variety of dimension
will denote a non-singular projective algebraic variety of dimension  over an algebraically closed field
over an algebraically closed field  . If
. If 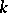 is the field of complex numbers
is the field of complex numbers 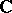 , then each algebraic cycle
, then each algebraic cycle 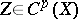 defines a
defines a 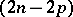 -dimensional homology class
-dimensional homology class 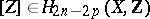 and, in accordance with Poincaré duality, a cohomology class
and, in accordance with Poincaré duality, a cohomology class 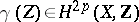 . The homology (or, respectively, cohomology) classes of type
. The homology (or, respectively, cohomology) classes of type 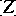 (or
(or  ) are called algebraic homology (respectively, cohomology) classes. (Hodge's conjecture) Each analytic cycle is homologous with an algebraic cycle. It is believed that an integral
) are called algebraic homology (respectively, cohomology) classes. (Hodge's conjecture) Each analytic cycle is homologous with an algebraic cycle. It is believed that an integral 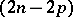 -dimensional cycle
-dimensional cycle 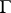 on
on 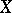 is homologous with an algebraic cycle if and only if the integrals of all closed differential forms of type
is homologous with an algebraic cycle if and only if the integrals of all closed differential forms of type 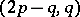 ,
, 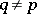 , over
, over 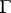 are equal to zero. This conjecture has only been proved for
are equal to zero. This conjecture has only been proved for 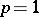 (for
(for 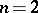 [6], and for all
[6], and for all  [7]), for
[7]), for 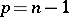 , and for isolated classes of varieties [4].
, and for isolated classes of varieties [4].
If 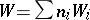 is an algebraic cycle on the product of two varieties
is an algebraic cycle on the product of two varieties 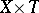 , then the set of cycles on
, then the set of cycles on 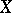 of the form
of the form
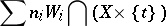 |
is known as a family of algebraic cycles on 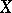 parametrized by the base
parametrized by the base 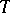 . The usual requirement in this connection is that the projection of each subvariety
. The usual requirement in this connection is that the projection of each subvariety 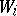 on
on 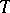 be a flat morphism. If
be a flat morphism. If 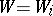 is defined by an irreducible subvariety, the corresponding family of algebraic cycles on
is defined by an irreducible subvariety, the corresponding family of algebraic cycles on 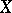 is called a family of algebraic subvarieties. In particular, for any flat morphism
is called a family of algebraic subvarieties. In particular, for any flat morphism 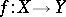 of algebraic varieties its fibres
of algebraic varieties its fibres 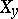 form a family of algebraic subvarieties of
form a family of algebraic subvarieties of 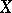 parametrized by the base
parametrized by the base 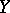 . A second particular case of this concept is that of a linear system. All members of a family of algebraic subvarieties (or, respectively, algebraic cycles) of a projective variety
. A second particular case of this concept is that of a linear system. All members of a family of algebraic subvarieties (or, respectively, algebraic cycles) of a projective variety 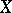 , parametrized by a connected base, have the same Hilbert polynomial (respectively, virtual arithmetic genus).
, parametrized by a connected base, have the same Hilbert polynomial (respectively, virtual arithmetic genus).
Two algebraic cycles 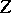 and
and 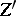 on a variety
on a variety 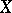 are algebraically equivalent (which is denoted by
are algebraically equivalent (which is denoted by 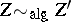 ) if they belong to the same family, parametrized by a connected base. Intuitively, equivalence of algebraic cycles means that
) if they belong to the same family, parametrized by a connected base. Intuitively, equivalence of algebraic cycles means that 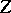 may be algebraically deformed into
may be algebraically deformed into 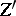 . If this definition includes the condition that the base
. If this definition includes the condition that the base 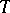 is a rational variety, the algebraic cycles
is a rational variety, the algebraic cycles 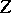 and
and 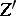 are called rationally equivalent (which is denoted by
are called rationally equivalent (which is denoted by 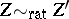 ). If
). If 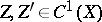 , the concept of rational equivalence reduces to the concept of linear equivalence of divisors. The subgroup of algebraic cycles rationally (or, respectively, algebraically) equivalent to zero, is denoted by
, the concept of rational equivalence reduces to the concept of linear equivalence of divisors. The subgroup of algebraic cycles rationally (or, respectively, algebraically) equivalent to zero, is denoted by 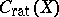 (respectively,
(respectively, 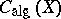 ). Each of these groups is a direct sum of its components
). Each of these groups is a direct sum of its components
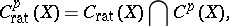 |
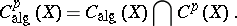 |
The quotient group 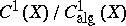 is finitely generated and is called as the Neron–Severi group of the variety
is finitely generated and is called as the Neron–Severi group of the variety 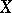 . The problem of the quotient group
. The problem of the quotient group 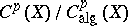 being finitely generated for
being finitely generated for 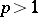 remains open at the time of writing (1977). The quotient group
remains open at the time of writing (1977). The quotient group 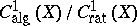 has the structure of an Abelian variety (cf. Picard scheme). The operation of intersection of cycles makes it possible to define a multiplication in the quotient group
has the structure of an Abelian variety (cf. Picard scheme). The operation of intersection of cycles makes it possible to define a multiplication in the quotient group 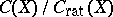 , converting it into a commutative ring, called the Chow ring of the variety
, converting it into a commutative ring, called the Chow ring of the variety 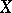 (cf. Intersection theory).
(cf. Intersection theory).
For any Weil cohomology theory 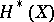 there exists a uniquely defined homomorphism of groups
there exists a uniquely defined homomorphism of groups
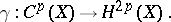 |
Two algebraic cycles 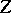 and
and 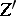 are called homologically equivalent (which is denoted by
are called homologically equivalent (which is denoted by 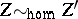 ) if
) if 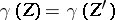 . The subgroup of algebraic cycles that are homologically equivalent with zero is denoted by
. The subgroup of algebraic cycles that are homologically equivalent with zero is denoted by 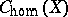 . The imbedding
. The imbedding 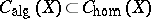 is valid. The quotient group
is valid. The quotient group 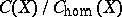 is finitely generated, and is a subring in the ring
is finitely generated, and is a subring in the ring 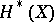 , which is denoted by
, which is denoted by 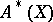 and is known as the ring of algebraic Weil cohomology classes. It is not known (1986) whether or not
and is known as the ring of algebraic Weil cohomology classes. It is not known (1986) whether or not 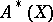 depends on the Weil cohomology theory that has been chosen.
depends on the Weil cohomology theory that has been chosen.
Two algebraic cycles 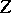 and
and 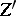 are called
are called  -equivalent (which is denoted by
-equivalent (which is denoted by 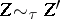 ) if there exists an
) if there exists an 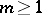 such that
such that 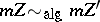 . The subgroup of algebraic cycles that are
. The subgroup of algebraic cycles that are  -equivalent to zero, is denoted by
-equivalent to zero, is denoted by 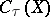 . Two algebraic cycles
. Two algebraic cycles  and
and 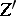 from
from  are called numerically equivalent (which is denoted by
are called numerically equivalent (which is denoted by 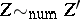 ) if the equality
) if the equality 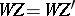 is valid for any
is valid for any 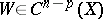 , provided both sides of the equality are defined. The subgroup of algebraic cycles numerically equivalent with zero is denoted by
, provided both sides of the equality are defined. The subgroup of algebraic cycles numerically equivalent with zero is denoted by 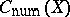 . The imbeddings
. The imbeddings
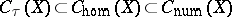 |
are valid. For divisors the groups 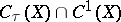 ,
, 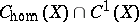 and
and 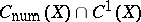 are identical [6]. However, in accordance with the counterexample in [5] for the case
are identical [6]. However, in accordance with the counterexample in [5] for the case 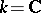
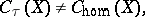 |
where 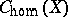 is considered with respect to the ordinary cohomology theory with rational coefficients. A similar counterexample was established for a field
is considered with respect to the ordinary cohomology theory with rational coefficients. A similar counterexample was established for a field 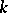 of arbitrary characteristic and for the
of arbitrary characteristic and for the 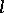 -adic theory of Weil cohomology. The question as to the equality of the groups
-adic theory of Weil cohomology. The question as to the equality of the groups 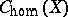 and
and 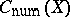 has been solved [9].
has been solved [9].
Let 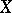 be imbedded in a projective space and let
be imbedded in a projective space and let 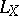 be the cohomology class of a hyperplane section. An algebraic cohomology class
be the cohomology class of a hyperplane section. An algebraic cohomology class
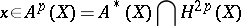 |
is called primitive if 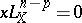 . In such a case, if
. In such a case, if 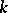 is the field of complex numbers
is the field of complex numbers  , the bilinear form
, the bilinear form
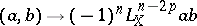 |
is positive definite on the subspace of primitive classes in 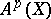 . A similar proposition for arbitrary
. A similar proposition for arbitrary 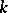 , which is closely connected with the Weil conjectures on the zeta-function of an algebraic variety, has been proved for
, which is closely connected with the Weil conjectures on the zeta-function of an algebraic variety, has been proved for 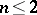 only.
only.
If a variety 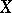 is defined over a field
is defined over a field 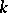 that is not algebraically closed, the Galois group
that is not algebraically closed, the Galois group 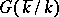 of the separable algebraic closure of the field
of the separable algebraic closure of the field 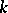 acts on the Weil cohomology
acts on the Weil cohomology 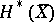 , where
, where 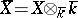 . Each element of
. Each element of  is invariant with respect to some subgroup of finite index of the group
is invariant with respect to some subgroup of finite index of the group 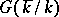 . It is believed (Tate's conjecture on algebraic cycles) that the converse proposition is also true if
. It is believed (Tate's conjecture on algebraic cycles) that the converse proposition is also true if 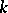 is finitely generated over its prime subfield. Many conjectures on the zeta-function of algebraic varieties are based on this assumption [2].
is finitely generated over its prime subfield. Many conjectures on the zeta-function of algebraic varieties are based on this assumption [2].
References
| [1] | M. Baldassarri, "Algebraic varieties" , Springer (1956) MR0082172 Zbl 0995.14003 Zbl 0075.15902 |
| [2] | J.T. Tate, "Algebraic cohomology classes" , Summer school of algebraic geometry Woods Hole, 1964 Zbl 0213.22901 |
| [3] | I.V. Dolgachev, V.A. Iskovskikh, "Geometry of algebraic varieties" J. Soviet Math. , 5 : 6 (1976) pp. 803–864 Itogi Nauk. i Tekhn. Algebra Topol. Geom. , 12 (1974) pp. 77–170 |
| [4] | S.L. Kleiman, "Algebraic cycles and the Weil conjecture" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , Dix exposés sur la cohomologie des schémas , North-Holland & Masson (1968) pp. 359–386 MR0292838 |
| [5] | P.A. Griffiths, "On the periods of certain rational integrals II" Ann. of Math. (2) , 90 : 3 (1969) pp. 496–541 Zbl 0215.08103 |
| [6] | S. Lefschetz, "L'analysis situs et la géométrie algébrique" , Gauthier-Villars (1924) MR0033557 MR1520618 |
| [7] | W.V.D. Hodge, "The theory and application of harmonic integrals" , Cambridge Univ. Press (1952) MR0051571 |
| [8] | "Groupes de monodromie en geometrie algebrique" M. Raynaud (ed.) D.S. Rim (ed.) A. Grothendieck (ed.) , Sem. Geom. Alg. , 7 , Springer (1972–1973) MR0354656 |
| [9] | P. Deligne, "La conjecture de Weil I" Publ. Math. IHES , 43 (1974) pp. 273–308 MR0340258 Zbl 0314.14007 Zbl 0287.14001 |
Comments
In 1983 H. Clemens proved that 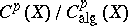 is not finitely generated [a1]. He also proved that
is not finitely generated [a1]. He also proved that 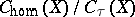 is not finitely generated, even after tensoring with the field of rational numbers [a1].
is not finitely generated, even after tensoring with the field of rational numbers [a1].
A state-of-the-art survey concerning the Hodge conjecture is in [a2]. See also [a3].
Much of the recent progress of the theory of algebraic cycles is related to algebraic 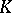 -theory, see [a4].
-theory, see [a4].
References
| [a1] | H. Clemens, "Homological equivalence modulo algebraic equivalence is not finitely generated" Publ. Math. IHES , 58 (1983) pp. 19–38 MR720930 Zbl 0529.14002 |
| [a2] | T. Shiado, "What is known about the Hodge conjecture" , North-Holland & Kinokuniya (1983) |
| [a3] | M.F. Atiyah, F. Hirzebruch, "Analytic cycles on complex manifolds" Topology , 1 (1961) pp. 25–45 MR0145560 Zbl 0108.36401 |
| [a4] | S. Bloch, "Lectures on algebraic cycles" , IV , Dept. Math. Duke Univ. (1980) MR0558224 Zbl 0436.14003 |
Algebraic cycle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algebraic_cycle&oldid=23745