Difference between revisions of "Algebra of functions"
(Importing text file) |
m (link) |
||
| Line 17: | Line 17: | ||
A function algebra is said to be a uniformly-convergent algebra (or uniform algebra) if the norm in this algebra defines a notion of convergence equivalent to the uniform convergence of the functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137045.png" /> on the space of maximal ideals. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137046.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137047.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137048.png" /> is a uniform algebra. The general example of a uniform algebra is a closed subalgebra of the algebra of bounded continuous functions on some topological space, provided with the natural sup-norm. | A function algebra is said to be a uniformly-convergent algebra (or uniform algebra) if the norm in this algebra defines a notion of convergence equivalent to the uniform convergence of the functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137045.png" /> on the space of maximal ideals. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137046.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137047.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137048.png" /> is a uniform algebra. The general example of a uniform algebra is a closed subalgebra of the algebra of bounded continuous functions on some topological space, provided with the natural sup-norm. | ||
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137049.png" /> is a uniform algebra and if its space of maximal ideals is metrizable, then among the boundaries (not only the closed ones) there is a minimal boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137050.png" />, the closure of which is the Shilov boundary. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137051.png" /> consists of "peak points" : <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137052.png" /> is a peak point if there exists a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137053.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137054.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137055.png" />. In the present case any point in the space of maximal ideals has a representing measure concentrated on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137056.png" />. | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137049.png" /> is a uniform algebra and if its space of maximal ideals is metrizable, then among the boundaries (not only the closed ones) there is a minimal boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137050.png" />, the closure of which is the [[Shilov boundary]]. The set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137051.png" /> consists of "peak points" : <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137052.png" /> is a peak point if there exists a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137053.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137054.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137055.png" />. In the present case any point in the space of maximal ideals has a representing measure concentrated on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011370/a01137056.png" />. |
A function algebra is said to be analytic if all functions of this algebra that vanish on a non-empty open subset of the space of maximal ideals vanish identically. Algebras that are analytic with respect to the boundary are defined in a similar manner. Any analytic algebra is analytic with respect to the Shilov boundary; the converse is usually not true. | A function algebra is said to be analytic if all functions of this algebra that vanish on a non-empty open subset of the space of maximal ideals vanish identically. Algebras that are analytic with respect to the boundary are defined in a similar manner. Any analytic algebra is analytic with respect to the Shilov boundary; the converse is usually not true. | ||
Revision as of 13:45, 6 March 2018
function algebra
A semi-simple commutative Banach algebra 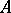 , realized as an algebra of continuous functions on the space of maximal ideals
, realized as an algebra of continuous functions on the space of maximal ideals 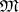 . If
. If 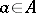 and if
and if 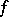 is some function defined on the spectrum of the element
is some function defined on the spectrum of the element  (i.e. on the set of values of the function
(i.e. on the set of values of the function 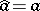 ), then
), then 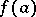 is some function on
is some function on 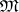 . Clearly, it is not necessarily true that
. Clearly, it is not necessarily true that 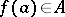 . If, however,
. If, however, 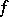 is an entire function, then
is an entire function, then 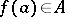 for any
for any 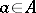 . The use of the Cauchy integral formula permits a considerable strengthening of this result: If the function
. The use of the Cauchy integral formula permits a considerable strengthening of this result: If the function 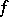 is analytic in some neighbourhood of the spectrum of the element
is analytic in some neighbourhood of the spectrum of the element  , then
, then 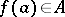 and the mapping
and the mapping 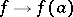 is a homomorphism of the algebra of functions which are analytic in some neighbourhood of the spectrum of
is a homomorphism of the algebra of functions which are analytic in some neighbourhood of the spectrum of 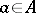 into
into  . This proposition is valid for non-semi-simple commutative Banach algebras as well. Moreover, this class of functions that are analytic in a neighbourhood of the spectrum of a given element cannot be enlarged, in general. For example, if
. This proposition is valid for non-semi-simple commutative Banach algebras as well. Moreover, this class of functions that are analytic in a neighbourhood of the spectrum of a given element cannot be enlarged, in general. For example, if 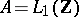 and
and 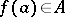 for all
for all 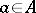 with spectrum in the interval
with spectrum in the interval 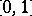 , then
, then 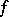 is analytic in some neighbourhood of this interval.
is analytic in some neighbourhood of this interval.
In a few cases 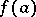 can also be defined for multi-valued analytic functions
can also be defined for multi-valued analytic functions 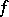 , but such a definition has inherent difficulties. Thus, let
, but such a definition has inherent difficulties. Thus, let 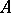 be the algebra of continuous functions in the disc
be the algebra of continuous functions in the disc 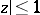 that are analytic in the disc
that are analytic in the disc 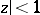 and that satisfy the condition
and that satisfy the condition 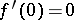 . The unit disc is naturally identified with the space of maximal ideals of
. The unit disc is naturally identified with the space of maximal ideals of 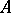 . The function
. The function 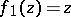 , which is continuous on the space of maximal ideals, does not belong to
, which is continuous on the space of maximal ideals, does not belong to 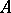 , but is a solution of the quadratic equation
, but is a solution of the quadratic equation
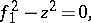 |
where  .
.
If 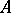 is a semi-simple algebra with space of maximal ideals
is a semi-simple algebra with space of maximal ideals 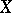 , if
, if 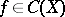 and if
and if
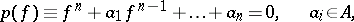 |
with 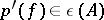 , the group of units of
, the group of units of 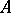 (a simple root), then
(a simple root), then 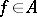 . Similarly, if
. Similarly, if  and if
and if 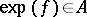 , then
, then 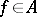 .
.
A function algebra is said to be a uniformly-convergent algebra (or uniform algebra) if the norm in this algebra defines a notion of convergence equivalent to the uniform convergence of the functions 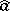 on the space of maximal ideals. If
on the space of maximal ideals. If 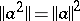 for all
for all 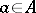 , then
, then 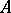 is a uniform algebra. The general example of a uniform algebra is a closed subalgebra of the algebra of bounded continuous functions on some topological space, provided with the natural sup-norm.
is a uniform algebra. The general example of a uniform algebra is a closed subalgebra of the algebra of bounded continuous functions on some topological space, provided with the natural sup-norm.
If 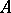 is a uniform algebra and if its space of maximal ideals is metrizable, then among the boundaries (not only the closed ones) there is a minimal boundary
is a uniform algebra and if its space of maximal ideals is metrizable, then among the boundaries (not only the closed ones) there is a minimal boundary 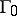 , the closure of which is the Shilov boundary. The set
, the closure of which is the Shilov boundary. The set 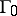 consists of "peak points" :
consists of "peak points" : 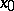 is a peak point if there exists a function
is a peak point if there exists a function 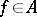 such that
such that  for all
for all 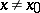 . In the present case any point in the space of maximal ideals has a representing measure concentrated on
. In the present case any point in the space of maximal ideals has a representing measure concentrated on 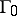 .
.
A function algebra is said to be analytic if all functions of this algebra that vanish on a non-empty open subset of the space of maximal ideals vanish identically. Algebras that are analytic with respect to the boundary are defined in a similar manner. Any analytic algebra is analytic with respect to the Shilov boundary; the converse is usually not true.
A function algebra 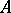 is said to be regular if, for any closed set
is said to be regular if, for any closed set 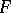 in the space
in the space 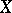 of maximal ideals of
of maximal ideals of  and for any point
and for any point 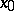 not contained in
not contained in 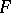 , it is possible to find a function
, it is possible to find a function 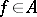 such that
such that 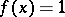 for all
for all 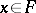 and
and  . All regular algebras are normal, i.e. for any pair of non-intersecting closed sets
. All regular algebras are normal, i.e. for any pair of non-intersecting closed sets 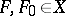 there exists an element
there exists an element 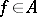 such that
such that 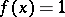 for all
for all 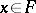 and
and 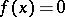 for all
for all 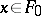 . In a regular algebra, for any finite open covering
. In a regular algebra, for any finite open covering 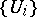 ,
, 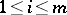 , of the space
, of the space 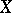 there exists a partition of unity belonging to
there exists a partition of unity belonging to 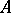 , i.e. a system of functions
, i.e. a system of functions 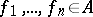 for which
for which
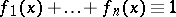 |
and
 |
A function 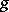 is said to belong locally to the function algebra
is said to belong locally to the function algebra 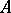 if for any point
if for any point 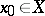 there exists a neighbourhood in which this function coincides with some function of the algebra. Any function which locally belongs to a regular algebra is itself an element of this algebra.
there exists a neighbourhood in which this function coincides with some function of the algebra. Any function which locally belongs to a regular algebra is itself an element of this algebra.
An element  of a function algebra is called real if
of a function algebra is called real if 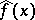 is real for all
is real for all 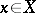 . If
. If 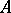 is an algebra with real generators
is an algebra with real generators  and if
and if
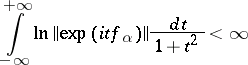 |
for all 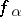 , then
, then 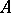 is regular.
is regular.
An ideal in a Banach algebra is said to be primary if it is contained in only one maximal ideal. If 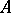 is a regular function algebra, then each maximal ideal
is a regular function algebra, then each maximal ideal 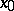 contains a smallest closed primary ideal
contains a smallest closed primary ideal 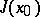 which is contained in any closed primary ideal contained in
which is contained in any closed primary ideal contained in 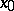 . The ideal
. The ideal 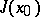 is the closure of the ideal formed by the functions
is the closure of the ideal formed by the functions 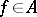 that vanish in some neighbourhood (depending on
that vanish in some neighbourhood (depending on 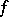 ) of
) of 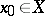 .
.
In the algebra of absolutely convergent Fourier series with an adjoined identity any maximal ideal coincides with the corresponding primary ideal.
Let 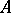 be a closed subalgebra of the algebra
be a closed subalgebra of the algebra 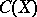 , where
, where 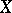 is a compactum (which does not necessarily coincide with the space of maximal ideals of
is a compactum (which does not necessarily coincide with the space of maximal ideals of 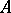 ). Let
). Let 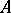 separate the points of
separate the points of 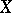 , i.e. for any two different points
, i.e. for any two different points 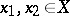 there exists a function
there exists a function 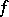 in
in 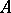 for which
for which 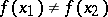 . The algebra
. The algebra 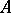 is called symmetric if both a function
is called symmetric if both a function 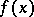 and the function
and the function 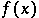 belong to it. According to the Stone–Weierstrass theorem, if
belong to it. According to the Stone–Weierstrass theorem, if 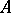 is symmetric, then
is symmetric, then 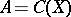 . The algebra
. The algebra 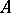 called anti-symmetric if it follows from the conditions
called anti-symmetric if it follows from the conditions 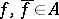 that
that 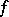 is a constant function. In particular, algebras of analytic functions are anti-symmetric. A subset
is a constant function. In particular, algebras of analytic functions are anti-symmetric. A subset 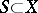 is called a set of anti-symmetry (with respect to the algebra
is called a set of anti-symmetry (with respect to the algebra 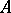 ) if any function
) if any function  that is real on
that is real on 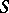 is constant on this set. It follows from this definition that the algebra
is constant on this set. It follows from this definition that the algebra  is anti-symmetric if the whole set
is anti-symmetric if the whole set 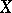 is a set of anti-symmetry. In the general case the space
is a set of anti-symmetry. In the general case the space 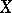 can be represented as the union of non-intersecting, closed, maximal sets of anti-symmetry. Each maximal set of anti-symmetry is an intersection of peak sets (a set
can be represented as the union of non-intersecting, closed, maximal sets of anti-symmetry. Each maximal set of anti-symmetry is an intersection of peak sets (a set 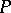 is called a peak set if there exists a function
is called a peak set if there exists a function 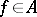 such that
such that 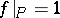 and
and 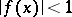 if
if 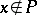 ). It follows that the restriction
). It follows that the restriction 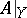 of the algebra
of the algebra 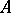 to a maximal set of anti-symmetry is a closed (anti-symmetric) subalgebra of the algebra
to a maximal set of anti-symmetry is a closed (anti-symmetric) subalgebra of the algebra 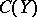 . If
. If 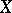 is the space of maximal ideals of the algebra
is the space of maximal ideals of the algebra 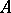 , the maximal sets of anti-symmetry are connected. If a continuous function is such that on each maximal set of anti-symmetry it coincides with some function in the algebra
, the maximal sets of anti-symmetry are connected. If a continuous function is such that on each maximal set of anti-symmetry it coincides with some function in the algebra 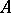 , then the function itself belongs to
, then the function itself belongs to 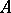 . This generalization of the Stone–Weierstrass theorem makes it possible, in principle, to reduce the study of arbitrary uniform algebras to the study of anti-symmetric algebras
. This generalization of the Stone–Weierstrass theorem makes it possible, in principle, to reduce the study of arbitrary uniform algebras to the study of anti-symmetric algebras 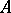 . However, the study of arbitrary algebras
. However, the study of arbitrary algebras 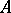 cannot be reduced to the study of analytic algebras: There exists an example of an algebra of type
cannot be reduced to the study of analytic algebras: There exists an example of an algebra of type  (a closed subalgebra of the algebra
(a closed subalgebra of the algebra  ) which does not coincide with
) which does not coincide with 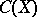 , and is anti-symmetric and regular.
, and is anti-symmetric and regular.
Let 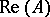 be the real space of functions of the form
be the real space of functions of the form 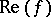 , where
, where 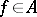 ; if
; if 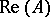 is an algebra or if
is an algebra or if 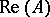 is closed in
is closed in 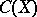 , then
, then 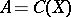 . The space
. The space 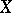 can be regarded as a part of the space of maximal ideals of the algebra
can be regarded as a part of the space of maximal ideals of the algebra 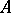 ; accordingly, not only the ordinary topology of the space of maximal ideals, but also the metric induced by the imbedding of
; accordingly, not only the ordinary topology of the space of maximal ideals, but also the metric induced by the imbedding of 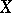 into the dual space to
into the dual space to 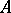 can be considered on
can be considered on 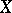 . The distance in the sense of this metric will be denoted by
. The distance in the sense of this metric will be denoted by  . For any points
. For any points 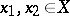 the inequality
the inequality 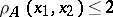 is valid; the relation
is valid; the relation 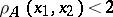 is an equivalence relation, and the equivalence classes are known as Gleason parts. If
is an equivalence relation, and the equivalence classes are known as Gleason parts. If 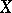 is the disc
is the disc  and
and 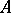 is the closed subalgebra in
is the closed subalgebra in 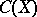 consisting of the functions analytic in
consisting of the functions analytic in 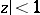 , then the metric
, then the metric  is non-Euclidean, and the one-point sets on the circle and in the interior of the disc serve as the Gleason parts. Gleason parts do not necessarily have an analytic structure: Any
is non-Euclidean, and the one-point sets on the circle and in the interior of the disc serve as the Gleason parts. Gleason parts do not necessarily have an analytic structure: Any 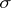 -compact completely-regular space is homeomorphic to the Gleason part of the space of maximal ideals of some algebra, such that the restriction of the algebra to this part contains all bounded continuous functions. The fact that two points belong to the same Gleason part can be described in terms of the representing measures on the Shilov boundary: Two such points have two mutually absolutely continuous representing measures with bounded derivatives. An algebra for which
-compact completely-regular space is homeomorphic to the Gleason part of the space of maximal ideals of some algebra, such that the restriction of the algebra to this part contains all bounded continuous functions. The fact that two points belong to the same Gleason part can be described in terms of the representing measures on the Shilov boundary: Two such points have two mutually absolutely continuous representing measures with bounded derivatives. An algebra for which 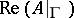 is dense in
is dense in 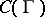 is called a Dirichlet algebra; if
is called a Dirichlet algebra; if 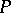 is a Gleason part in the space of maximal ideals of a Dirichlet algebra which contains more than one point, then there exists a continuous one-to-one mapping
is a Gleason part in the space of maximal ideals of a Dirichlet algebra which contains more than one point, then there exists a continuous one-to-one mapping 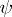 of the disc
of the disc 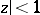 into
into 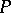 such that for any function
such that for any function 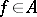 the function
the function 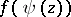 is analytic in
is analytic in 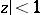 . Thus,
. Thus, 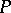 has a structure with respect to which the functions
has a structure with respect to which the functions  are analytic; the mapping
are analytic; the mapping 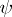 is not a homeomorphism in general if
is not a homeomorphism in general if 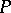 is endowed with the ordinary topology of the space of maximal ideals, but
is endowed with the ordinary topology of the space of maximal ideals, but 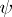 is a homeomorphism if
is a homeomorphism if 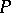 is endowed with the metric
is endowed with the metric 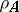 .
.
For references see Banach algebra.
Comments
References
| [a1] | T.W. Gamelin, "Uniform algebras" , Prentice-Hall (1969) |
| [a2] | E.L. Stout, "The theory of uniform algebras" , Bogden & Quigley (1971) |
Algebra of functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algebra_of_functions&oldid=14555