Adjoint semi-group of operators
The semi-group on a dual Banach space 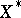 composed of the adjoint operators of a
composed of the adjoint operators of a 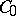 -semi-group on
-semi-group on  (cf. also Semi-group of operators).
(cf. also Semi-group of operators).
Let 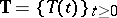 be a
be a 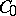 -semi-group on a Banach space
-semi-group on a Banach space  , i.e.
, i.e. 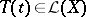 for all
for all 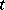 and
and
i) 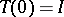 , the identity operator on
, the identity operator on  ;
;
ii) 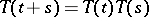 for all
for all 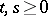 ;
;
iii) the orbits 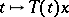 are strongly continuous (cf. Strongly-continuous semi-group) on
are strongly continuous (cf. Strongly-continuous semi-group) on 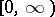 for all
for all 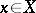 . On the dual space
. On the dual space 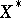 , the adjoint semi-group
, the adjoint semi-group 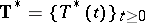 , with
, with 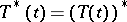 , satisfies i) and ii), but not necessarily iii). Therefore one defines
, satisfies i) and ii), but not necessarily iii). Therefore one defines
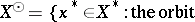 |
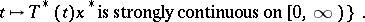 |
This is a norm-closed, weak -dense,
-dense, 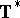 -invariant subspace of
-invariant subspace of 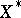 , and the restriction
, and the restriction 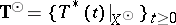 is a
is a 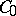 -semi-group on
-semi-group on  , called the strongly continuous adjoint of
, called the strongly continuous adjoint of 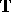 . Its infinitesimal generator
. Its infinitesimal generator 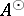 is the part of
is the part of  in
in 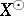 , where
, where 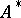 is the adjoint of the infinitesimal generator
is the adjoint of the infinitesimal generator  of
of 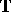 . Its spectrum satisfies
. Its spectrum satisfies 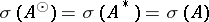 . If
. If  is reflexive (cf. Reflexive space), then
is reflexive (cf. Reflexive space), then 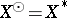 [a9].
[a9].
Starting from 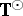 , one defines
, one defines  and
and 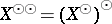 . The natural mapping
. The natural mapping 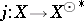 ,
, 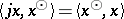 , is an isomorphic imbedding with values in
, is an isomorphic imbedding with values in 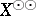 , and
, and 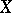 is said to be
is said to be  -reflexive with respect to
-reflexive with respect to 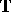 if
if 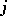 maps
maps  onto
onto  . This is the case if and only if the resolvent
. This is the case if and only if the resolvent 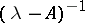 is weakly compact for some (hence for all)
is weakly compact for some (hence for all) 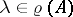 [a7]. If
[a7]. If  is
is  -reflexive with respect to
-reflexive with respect to 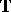 and
and 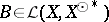 , then the part of
, then the part of 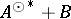 in
in  generates a
generates a 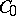 -semi-group on
-semi-group on  [a1].
[a1].
Let 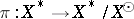 be the quotient mapping. If, for some
be the quotient mapping. If, for some 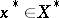 , the mapping
, the mapping 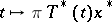 is separably-valued, then
is separably-valued, then 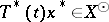 for all
for all 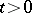 . Hence, if
. Hence, if  extends to a
extends to a  -group, then
-group, then 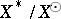 is either trivial or non-separable [a4].
is either trivial or non-separable [a4].
If  is a positive
is a positive 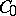 -semi-group on a Banach lattice
-semi-group on a Banach lattice  , then
, then 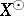 need not be a sublattice of
need not be a sublattice of 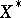 [a2]. If, however,
[a2]. If, however, 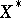 has order-continuous norm, then
has order-continuous norm, then 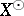 is even a projection band in
is even a projection band in 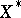 [a8]. For a positive
[a8]. For a positive  -semi-group
-semi-group 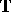 on an arbitrary Banach lattice
on an arbitrary Banach lattice 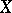 one has
one has
 |
for all 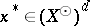 , the disjoint complement of
, the disjoint complement of 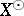 in
in 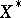 . If
. If 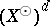 has a weak order unit, then for all
has a weak order unit, then for all 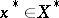 and
and 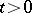 one has
one has 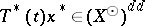 , the band generated by
, the band generated by 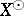 in
in 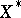 [a5]. If, for some
[a5]. If, for some  , the mapping
, the mapping 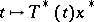 is weakly measurable, then, assuming the Martin axiom (cf. Suslin hypothesis), for all
is weakly measurable, then, assuming the Martin axiom (cf. Suslin hypothesis), for all 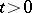 one has
one has 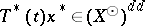 [a6].
[a6].
A general reference is [a3].
References
| [a1] | Ph. Clément, O. Diekmann, M. Gyllenberg, H.J.A.M. Heijmans, H.R. Thieme, "Perturbation theory for dual semigroups, Part I: The sun-reflexive case" Math. Ann. , 277 (1987) pp. 709–725 |
| [a2] | A. Grabosch, R. Nagel, "Order structure of the semigroup dual: A counterexample" Indagationes Mathematicae , 92 (1989) pp. 199–201 |
| [a3] | J.M.A.M. van Neerven, "The adjoint of a semigroup of linear operators" , Lecture Notes in Mathematics , 1529 , Springer (1992) |
| [a4] | J.M.A.M. van Neerven, "A dichotomy theorem for the adjoint of a semigroup of operators" Proc. Amer. Math. Soc. , 119 (1993) pp. 765–774 |
| [a5] | J.M.A.M. van Neerven, B. de Pagter, "The adjoint of a positive semigroup" Comp. Math. , 90 (1994) pp. 99–118 |
| [a6] | J.M.A.M. van Neerven, B. de Pagter, A.R. Schep, "Weak measurability of the orbits of an adjoint semigroup" G. Ferreyra (ed.) G.R. Goldstein (ed.) F. Neubrander (ed.) , Evolution Equations , Lecture Notes in Pure and Appl. Math. , 168 , M. Dekker (1994) pp. 327–336 |
| [a7] | B. de Pagter, "A characterization of sun-reflexivity" Math. Ann. , 283 (1989) pp. 511–518 |
| [a8] | B. de Pagter, "A Wiener–Young type theorem for dual semigroups" Acta Appl. Math. 27 (1992) pp. 101–109 |
| [a9] | R.S. Phillips, "The adjoint semi-group" Pacific J. Math. , 5 (1955) pp. 269–283 |
Adjoint semi-group of operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Adjoint_semi-group_of_operators&oldid=18347