Additive arithmetic function
An arithmetic function of one argument that satisfies the following conditions for two relatively prime integers 
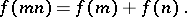 |
An additive arithmetic function is said to be strongly additive if 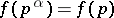 for all prime numbers
for all prime numbers 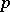 and all positive integers
and all positive integers 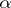 . An additive arithmetic function is said to be completely additive if the condition
. An additive arithmetic function is said to be completely additive if the condition 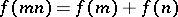 is satisfied for relatively non-prime integers
is satisfied for relatively non-prime integers 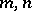 as well; in such a case
as well; in such a case 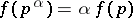 .
.
Examples. The function 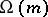 , which is the number of all prime divisors of the number
, which is the number of all prime divisors of the number 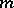 (multiple divisors are counted according to their multiplicity), is an additive arithmetic function; the function
(multiple divisors are counted according to their multiplicity), is an additive arithmetic function; the function 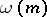 , which is the number of different prime divisors of the number
, which is the number of different prime divisors of the number 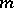 , is strongly additive; and the function
, is strongly additive; and the function 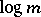 is completely additive.
is completely additive.
Comments
An arithmetic function is also called a number-theoretic function.
Additive arithmetic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Additive_arithmetic_function&oldid=17552